本文主要是介绍数学实验第三版（主编：李继成 赵小艳）课后练习答案（十二）（3），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
实验十二：微分方程模型
练习三
1.分别用数值解命令ode23t和ode45 计算示例3中微分方程的数值解,同用命令ode23 算得的数值解以及解析解比较,哪种方法精度较高?你用什么方法比较它们之间的精度?
clc;clear;
f=@(x,y)2*y+x+2;
figure(1)
[x,y]=ode23t(f,[1,2],1);
plot(x,y,'r');
[x,yy]=ode45(f,[1,2],1);
hold on
plot(x,yy,'b');
legend('ode23t','ode45');
[x,yyy]=ode23(f,[1,2],1);
figure(2)
plot(x,yyy);
syms y(x)
h=diff(y)==2*y+x+2;
hh=dsolve(h,y(0)==1);
hold on
ezplot(hh,[0,1]);
legend('数值解ode23','解析解');
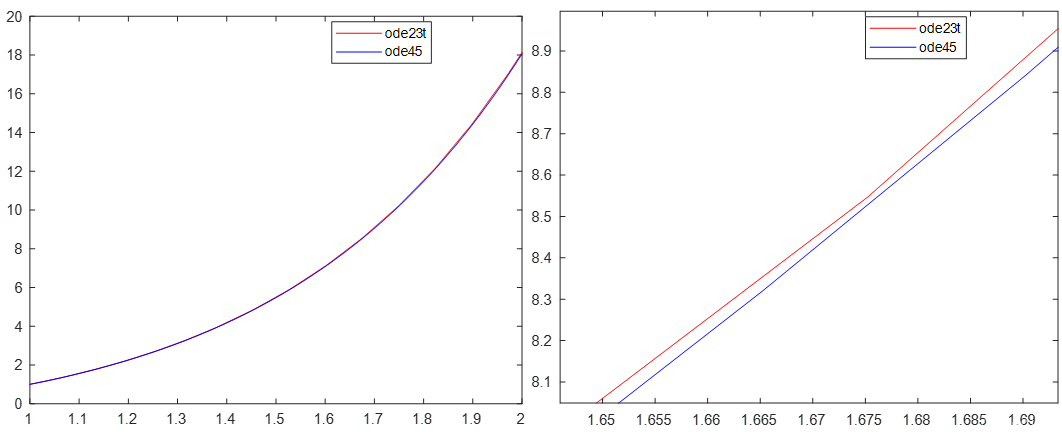
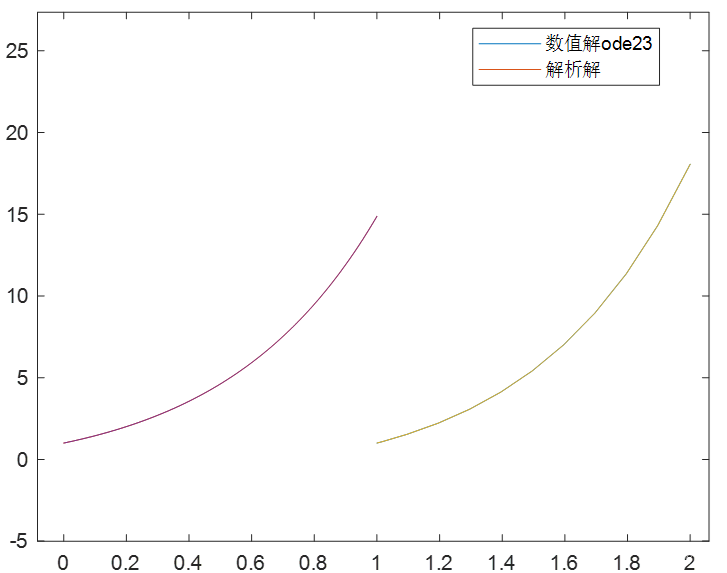
由上图我们可以发现，ode23所得到的数值解和解析解相差还是比较大的，而ode23t和ode45得到的数值解相差较小。
2.分别用命令ode23,ode23t和ode45求贝塞尔方程的数值解,并作出数值解曲线.
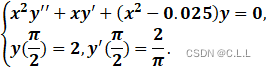
我们首先要将此微分方程改写为一阶方程（因为ode类函数只能解一阶可分离函数）：
令y'=z ,则原方程化为：
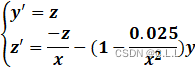
初值条件为：
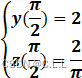
clc;clear;
f=@(x,m)[m(2);-m(2)/x-(1-(0.025/x^2)*m(1))];
[x,y]=ode23(f,[pi/2,2*pi],[2,2/pi]);
[xx,yy]=ode23t(f,[pi/2,2*pi],[2,2/pi]);
[xxx,yyy]=ode45(f,[pi/2,2*pi],[2,2/pi]);
figure(1)
plot(x,y);
figure(2)
plot(xx,yy);
figure(3)
plot(xxx,yyy);
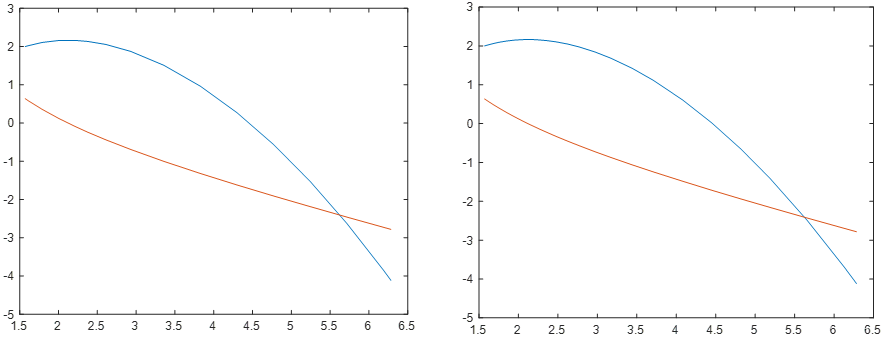
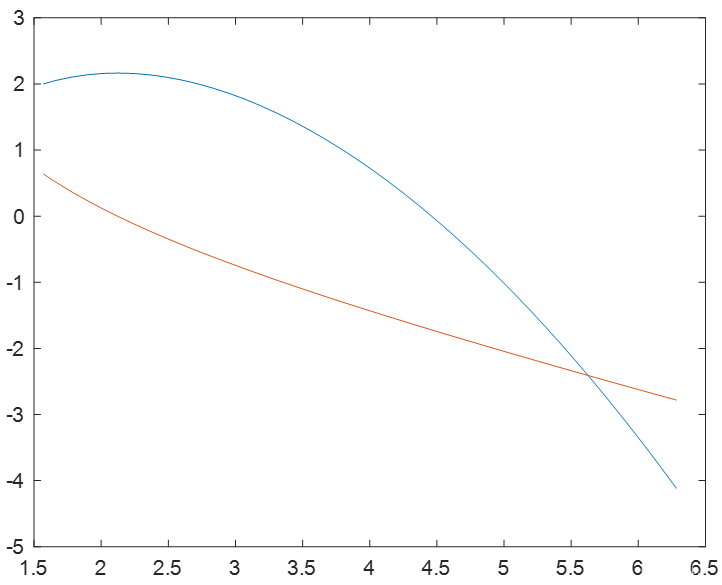
| x = 1.5708 1.6076 1.7914 2.0028 2.2100 2.3759 2.6091 2.9289 3.3577 3.8289 4.3001 4.7714 5.2426 5.7139 6.1851 6.2832 | y = 2.0000 0.6366 2.0225 0.5864 2.1086 0.3549 2.1583 0.1202 2.1615 -0.0861 2.1345 -0.2387 2.0552 -0.4382 1.8743 -0.6907 1.5104 -1.0022 0.9625 -1.3201 0.2691 -1.6204 -0.5627 -1.9084 -1.5280 -2.1874 -2.6232 -2.4596 -3.8453 -2.7265 -4.1155 -2.7815 | xx = 1.5708 1.5944 1.6415 1.6887 1.7479 1.8522 1.9564 2.0607 2.1280 2.1953 2.2626 2.3602 2.4785 2.6247 2.7709 2.9705 3.1701 3.4413 3.7126 4.0812 4.4497 4.8183 5.1869 5.6581 6.1294 6.2832 | yy = 2.0000 0.6366 2.0143 0.6046 2.0413 0.5416 2.0654 0.4809 2.0917 0.4073 2.1278 0.2846 2.1514 0.1694 2.1634 0.0605 2.1652 -0.0069 2.1625 -0.0722 2.1556 -0.1356 2.1380 -0.2247 2.1052 -0.3284 2.0483 -0.4512 1.9737 -0.5688 1.8448 -0.7225 1.6859 -0.8695 1.4242 -1.0608 1.1116 -1.2441 0.6089 -1.4833 0.0198 -1.7138 -0.6531 -1.9374 -1.4074 -2.1556 -2.4875 -2.4285 -3.6949 -2.6960 -4.1163 -2.7823 | xxx = 1.5708 1.5939 1.6170 1.6401 1.6632 1.7786 1.8941 2.0095 2.1250 2.2428 2.3606 2.4784 2.5962 2.7140 2.8319 2.9497 3.0675 3.1853 3.3031 3.4209 3.5387 3.6565 3.7743 3.8921 4.0100 4.1278 4.2456 4.3634 4.4812 4.5990 4.7168 4.8346 4.9524 5.0702 5.1880 5.3059 5.4237 5.5415 5.6593 5.7771 5.8949 5.9920 6.0890 6.1861 6.2832 | yyy = 2.0000 0.6366 2.0143 0.6049 2.0279 0.5738 2.0408 0.5432 2.0530 0.5132 2.1039 0.3701 2.1389 0.2374 2.1591 0.1132 2.1653 -0.0038 2.1581 -0.1171 2.1379 -0.2249 2.1053 -0.3282 2.0608 -0.4275 2.0047 -0.5234 1.9376 -0.6162 1.8596 -0.7064 1.7712 -0.7942 1.6726 -0.8800 1.5640 -0.9639 1.4455 -1.0461 1.3175 -1.1268 1.1801 -1.2061 1.0334 -1.2842 0.8776 -1.3612 0.7127 -1.4371 0.5390 -1.5121 0.3565 -1.5862 0.1653 -1.6596 -0.0345 -1.7322 -0.2428 -1.8042 -0.4596 -1.8755 -0.6847 -1.9462 -0.9181 -2.0164 -1.1598 -2.0861 -1.4097 -2.1554 -1.6676 -2.2242 -1.9337 -2.2926 -2.2078 -2.3606 -2.4899 -2.4283 -2.7799 -2.4956 -3.0779 -2.5626 -3.3293 -2.6176 -3.5861 -2.6724 -3.8481 -2.7270 -4.1155 -2.7814 |
此题要学会微分方程组该如何去解决。
3.17世纪末至18世纪初,牛顿发现在较小的温度范围内,物体冷却速率正比于该物体与环境温度的差值,因而得冷却模型
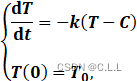
式中T(t)为物体t时刻的温度,C是环境温度,为正的常数,T0
为物体在=0时刻的温度,其解为
根据该冷却模型,完成下面的实验任务:
(1)某天晚上23:00时,在一住宅内发现一受害者的尸体,法医于23:35 赶到现场,立即测量死者体温是30.8℃,一小时后再次测量体温为29.1℃,法医还注意到当时室温是28℃,试估计受害者的死亡时间.
clc;clear;
format long
syms k m
f=@(t)9*exp(-k*t)+28;
f(m+35),f(m+95)
% 9*exp(-k*(m + 35)) + 28
% 9*exp(-k*(m + 95)) + 28
fsolve('fun',[1,5])
function f=fun(x)
f(1)=9*exp(-x(1)*(x(2) + 35)) + 28;
f(2)=9*exp(-x(1)*(x(2) + 95)) + 28;
end
ans =
4 3
由此可知，尸体的死亡时间为11:57.
(2)一个煮熟的鸡蛋在温度为98 ℃时放人温度为18℃的水中,5 min后鸡蛋的温度是 38℃,假设水的温度几乎没有升高,需要多长时间鸡蛋的温度可以达到20℃?
clc;clear;
format long
syms k m t
f=@(t)(98-18)*exp(-k*t)+18;
k=double(solve(f(5)==38));
k0=0.277258872223978;
f=@(t)(98-18)*exp(-k0*t)+18;
double(solve(f(t)==20))
ans =13.304820237218411；
4.承接此次实验中练习1的第2题,如图12.7所示.图中,两个容器完全相同,容器1排水孔的半径为0.02m,容器2排水孔的半径为0.01m,假如容器1装满水,容器2内水面的高度是1m,同时开启排水孔,完成下面的实验任务:
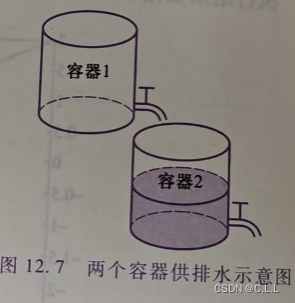
(1)经多长时间两个容器水面高度相同?
(2)求出容器2水面的高度与时间的函数关系,并求经多长时间容器2可以排空?
(3)在同一坐标系上画出两个容器内水面高度与时间的函数曲线进行比较.
(4)自己设定排水孔的半径与各容器的初始水位,将该容器排供水问题推广到n个容器的一般情况,建立一个简单的数学模型并求相关解.
我们假设水桶底面半径为1m，桶高4m；
clc;clear;
format short
m=4;r=1;
syms h(t) k
m1=-r^2*pi*diff(h)==k*sqrt(h)*pi*0.02^2;
h1=dsolve(m1,h(0)==m);
k=4.43;
h1=eval(h1(2))
%h1=((443*t)/500000 - 2)^2;
m2=-r^2*diff(h)==0.02^2*k*(2-(443*t)/500000)-0.01^2*k*sqrt(h);
h2=dsolve(m2)
f=@(t)(t - 1000000/443)^2/((500*67823512885646425253349271511524613553^(1/2))/3620155077721425633 + 62500/443)^2;
此题未写完，感觉不是很清楚，还请高人指点。
推荐下一篇文章：
数学实验第三版（主编：李继成 赵小艳）课后练习答案（十二）（4）
https://blog.csdn.net/2301_80199493/article/details/136136025?spm=1001.2014.3001.5501本文由作者自创，由于时间原因，难免出现些许错误，还请大家多多指正。创作不易，请大家多多支持。
这篇关于数学实验第三版（主编：李继成 赵小艳）课后练习答案（十二）（3）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
