本文主要是介绍P1990 覆盖墙壁题解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
有一个长为N宽为2的墙壁,给你两种砖头:一个长2宽1,另一个是L型覆盖3个单元的砖头。如下图:
0 0
0 00
砖头可以旋转,两种砖头可以无限制提供。你的任务是计算用这两种来覆盖N×2的墙壁的覆盖方法。例如一个2×3的墙可以有5种覆盖方法,如下:
012 002 011 001 011
012 112 022 011 001
注意可以使用两种砖头混合起来覆盖,如2×4的墙可以这样覆盖:
0112
0012
给定N,要求计算2×N的墙壁的覆盖方法。由于结果很大,所以只要求输出最后4位。例如2×13的覆盖方法为13465,只需输出3465即可。如果答案少于4位,就直接输出就可以,不用加前导0,如N=3时输出5。
输入输出格式
输入格式
一个整数N,表示墙壁的长。
输出格式
输出覆盖方法的最后4位,如果不足4位就输出整个答案。
输入输出样例
输入样例
13输出样例
3465解析
此题目采用递推,分好状态是一件非常重要的事情。使用F[N]表示铺满前N*2的面积的墙的方案数;“一列”指长为1,宽为2的墙壁。
1.当这面墙的最后一列被铺满时(如下图所示)

以这种状态结尾的方案数为F[N-1]。
2.当这面墙的最后两列被铺满时(如下图所示,注意颜色的区别)

以这种状态结尾的方案数为F[N-2]。
下面考虑L形的瓷砖,用数组G[N]来表示铺满前(N+1)*2的面积的墙,但是第(N+1)列有一个瓷砖已经被铺过(注意,是已经被铺过!)的方案数。
所以,下面这种情况的方案数就是G[N-2](因为实际上第N列已经铺满了,所以这里要处理的是前N-1列墙,所以多减了1)(如下图所示):
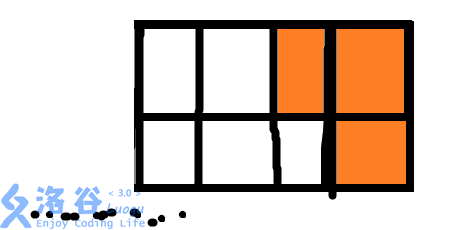
同理,这一种情况的方案数也是G[N-2]:

接下来解决,这个G数组应该怎么维护呢?
首先,第一种情况就是直接先让它变成一个长方形:
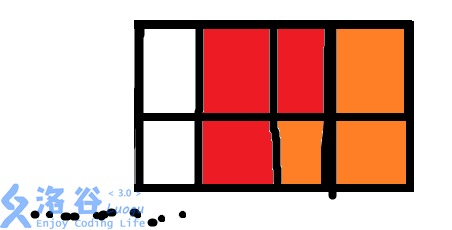
以这种状态结尾的方案数为F[N-3]。
第二种情况是,加上一块砖后,它仍然不是一个长方形:
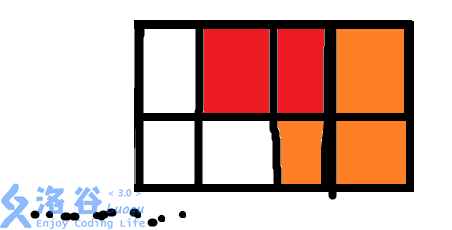
那么第二种情况的方案数就是G[N-3]。
所以,G[N-2](注意,不是G[N])的方案数就等于F[N-3]+G[N-3]。
化简得到:G[N]=F[N-1]+G[N-1]。
所以,F[N]的转移方程就是:
F[N]=F[N-1]+F[N-2]+2*G[N-2](前面说过G[N-2]的情况有两种)
而G[N]的转移方程就是:G[N]=F[N-1]+G[N-1]。
初始化:F[0]=1,G[0]=0;F[1]=G[1]=1;
#include<iostream>
using namespace std;
const int maxn=1000002;
const int mod=10000;
int f[maxn],g[maxn];
int main(){int n;cin>>n;f[0]=1;f[1]=g[1]=1;for(int i=2;i<=n;i++){f[i]=((f[i-1]+f[i-2])%mod+2*g[i-2]%mod)%mod;g[i]=(g[i-1]+f[i-1])%mod;}cout<<f[n];return 0;
}这篇关于P1990 覆盖墙壁题解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






