本文主要是介绍#7.21研究目标:预测510050股指期货未来收益率,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
import 需要用到的库
import pandas as pd
import numpy as np
product = 'IH'
stime = '093500'
etime = '145500'## load数据以及对数据做基本处理
data= pd.read_csv('IH_20230720.csv'.format(product), parse_dates=['Datetime'], index_col='Datetime',encoding='utf-8')#
print(data)
data.dtypes#注意这里的日期格式要求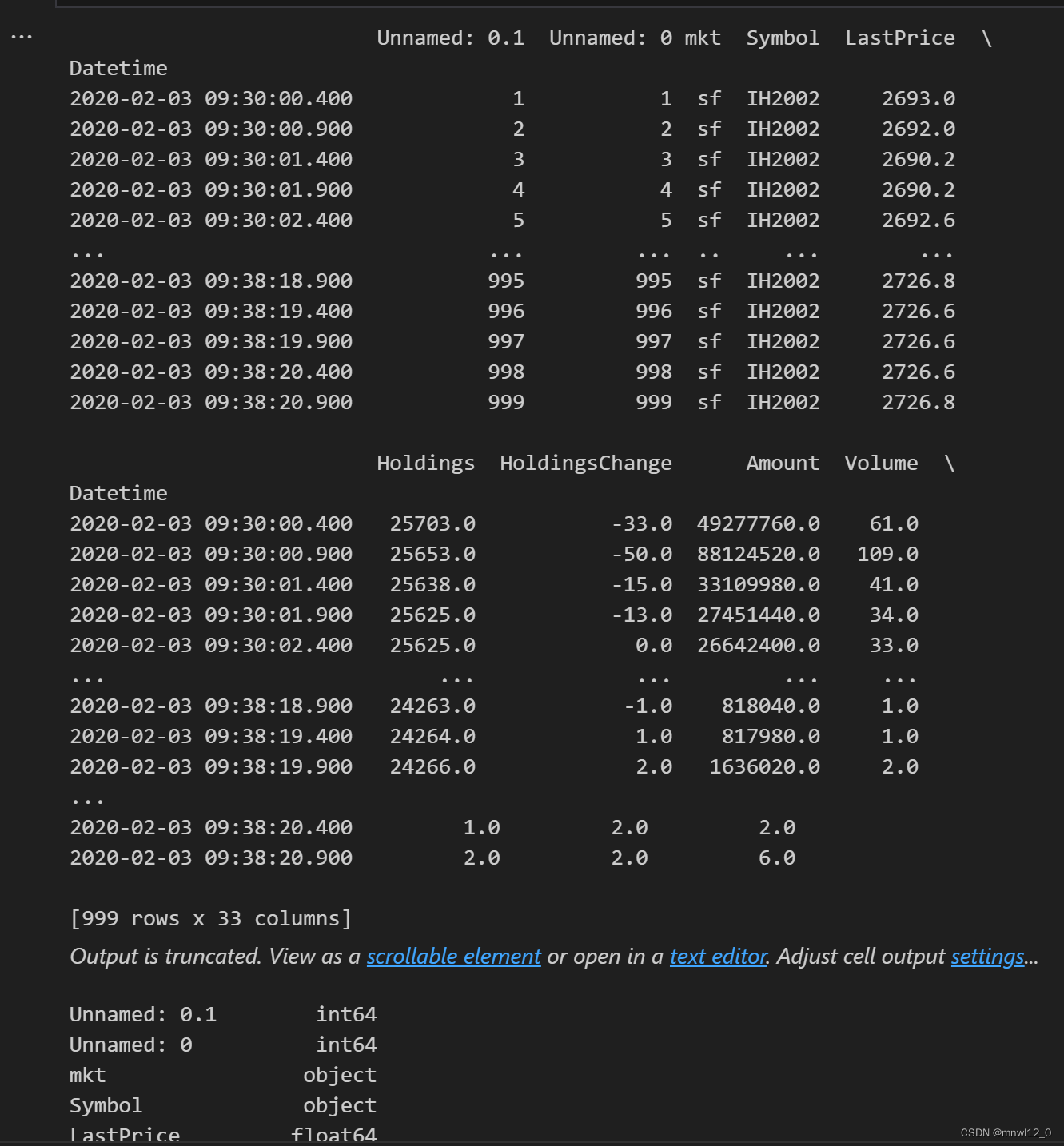
## 计算预测目标: 收益率
"""计算价格"""
IH_Price = (data['Bid1Price'] + data['Ask1Price'])/2
IH_Price"""计算rate of return"""
import math
RET=pd.DataFrame()
RET['return']=[math.log(IH_Price[i]/IH_Price[i-1]) for i in range(1,len(data['LastPrice']))]
RET_Index = pd.concat([RET, pd.Series(data.index[:-1])], axis=1)
RET_Index.set_index('Datetime', inplace=True)
RET_Index.dropna()"""
为什么用log return?
1. 对数收益率具有线性性质,这意味着对数收益率的加法等于对应收益率的乘法。这种线性性质使得对数收益率更易于处理和分析。
2. 对数收益率可以减小极端值的影响。金融市场中,收益率可能存在极端波动,使用对数收益率可以平滑这些波动,使得数据更加稳定,有助于建立更可靠的预测模型。
"""
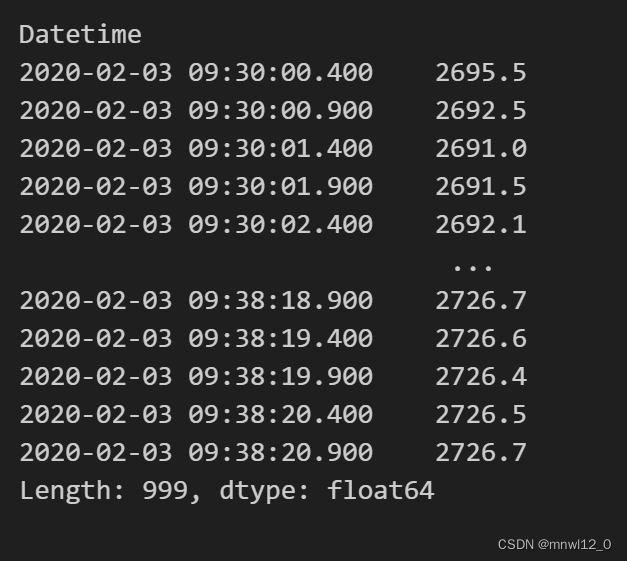
"""对收益率数据做初步处理"""
"""
我们需要对预测目标做初步的分析,包括:
1. 分布特点(矩)
2. 数值范围,包括最大最小,各分位数数值
3. 平稳性检验
4. 还有什么你们认为需要的
"""
print(RET.describe())
print(RET.std())
print(RET.skew())
print(RET.kurtosis())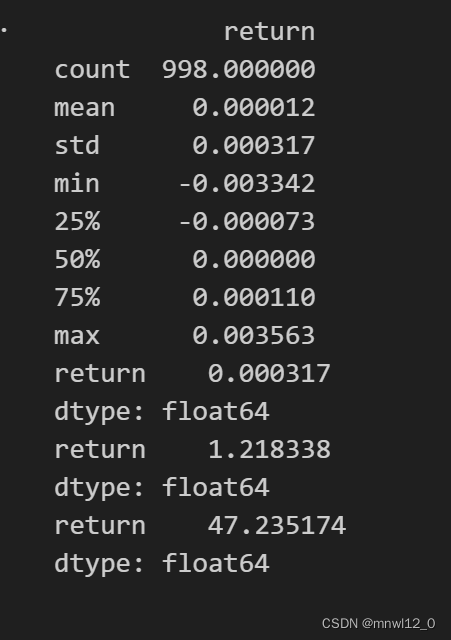
# 平稳性检验
import statsmodels.api as sm
import matplotlib.pyplot as pltplt.plot(RET['return'])
plt.show()
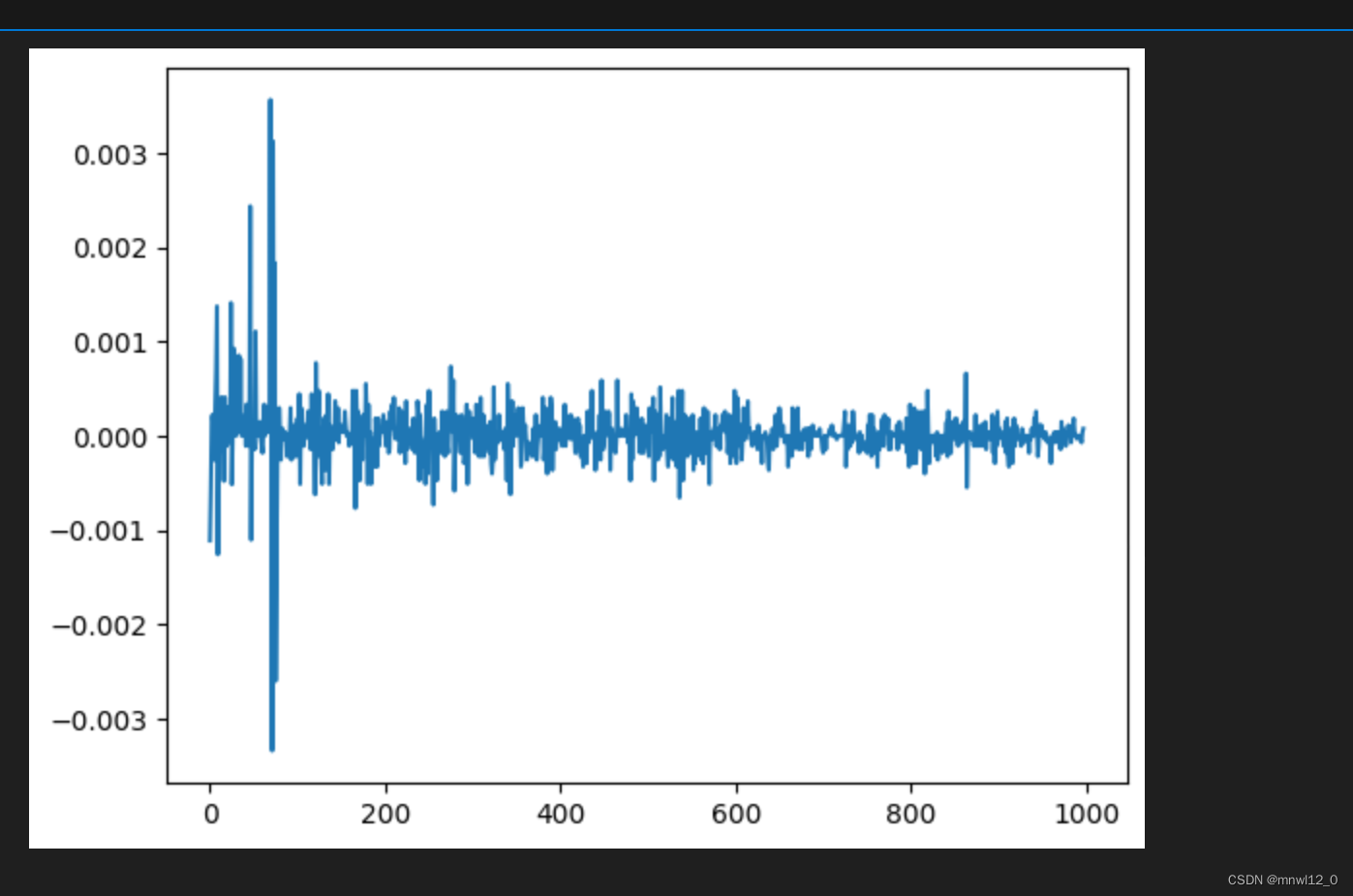
# 进行平稳性检验
mean = np.mean(RET['return'])
std = np.std(RET['return'])# 找出序列的极端值并替换为均值
for i in range(len(RET['return'])):if RET['return'][i] < mean - 3 * std or RET['return'][i] > mean + 3* std:RET['return'][i] = mean
plt.plot(RET['return'])
plt.show()adf_test = sm.tsa.adfuller(RET)
print('ADF Statistic: %f' % adf_test[0])
print('p-value: %f' % adf_test[1])
print('Critical Values:')
for key, value in adf_test[4].items():print('\t%s: %.3f' % (key, value))
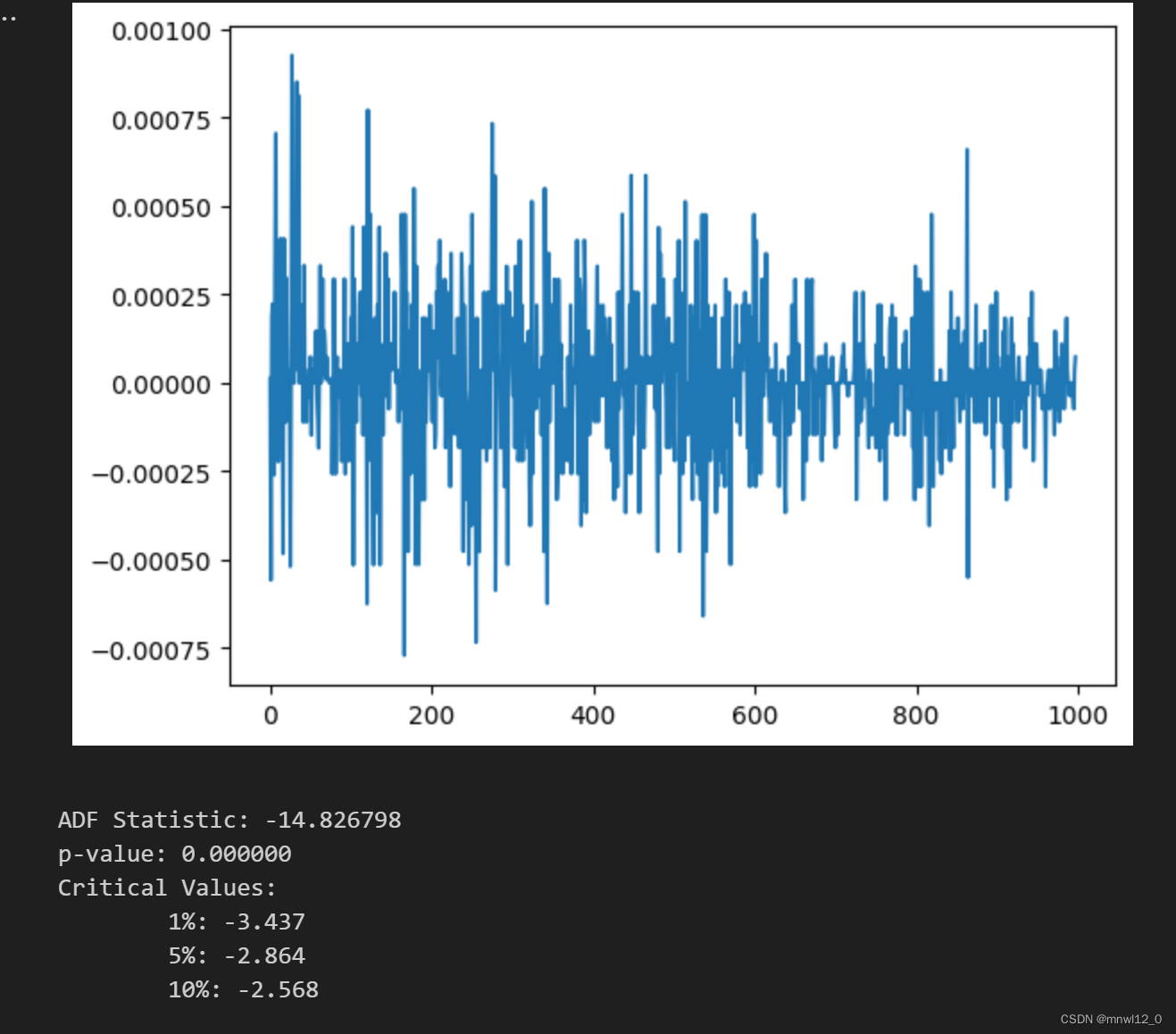
# 基于上述数据分析结论,可以看出收益率是非正态分布的,非平稳的。我们可以对收益率数据RET做差分
RET_diff = RET.diff(1).dropna()
RET_diff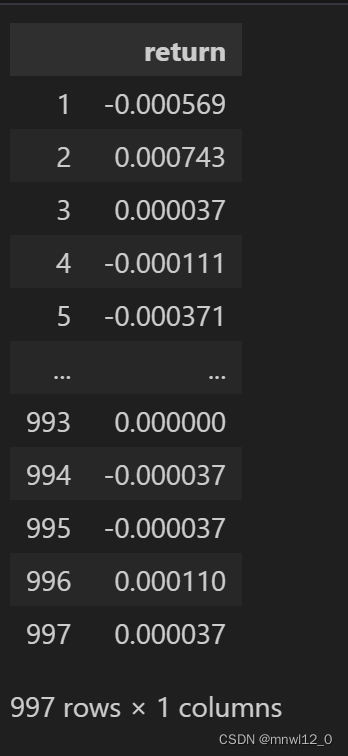
# 用numpy来计算skew和kurt
# 计算偏度
skewness = np.mean((RET - np.mean(RET))**3) / np.power(np.var(RET), 1.5)
print('Skewness:', skewness)# 计算峰度
kurtosis = np.mean((RET - np.mean(RET))**4) / np.power(np.var(RET), 2) - 3
print('Kurtosis:', kurtosis)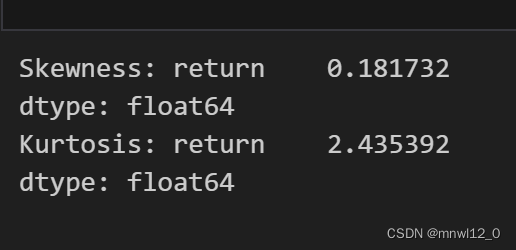
# 因子1: 加权平均价与成交价之差
def sig_theo2_price(data: pd.DataFrame, decay: float, stime: str, etime: str) ->pd.DataFrame:tmp_df = copy.deepcopy(data)tmp_df['bid_sz_total'] = tmp_df['Bid1Volume']+decay*tmp_df['Bid2Volume']+decay**2*tmp_df['Bid3Volume']tmp_df['ask_sz_total'] = tmp_df['Ask1Volume']+decay*tmp_df['Ask2Volume']+decay**2*tmp_df['Ask3Volume']tmp_df['bid_sz_total'][tmp_df['bid_sz_total']< 1] = 1tmp_df['ask_sz_total'][tmp_df['ask_sz_total']< 1] = 1tmp_df['bid_px_total'] = (tmp_df['Bid1Price']*tmp_df['Bid1Volume']+decay*tmp_df['Bid2Price']*tmp_df['Bid2Volume']+decay**2*tmp_df['Bid3Price']*tmp_df['Bid3Volume'])/tmp_df['bid_sz_total']tmp_df['ask_px_total'] = (tmp_df['Ask1Price']*tmp_df['Ask1Volume']+decay*tmp_df['Ask2Price']*tmp_df['Ask2Volume']+decay**2*tmp_df['Ask3Price']*tmp_df['Ask3Volume'])/tmp_df['ask_sz_total']tmp_df['theo_px'] = (tmp_df['bid_px_total']*tmp_df['ask_sz_total']+tmp_df['ask_px_total']*tmp_df['bid_sz_total'])/(tmp_df['bid_sz_total']+tmp_df['ask_sz_total'])tmp_df['sig_theo2_mid'] = tmp_df['theo_px'] - tmp_df['LastPrice']tmp_df = tmp_df[["sig_theo2_mid"]]tmp_df = pd.concat([tmp_df.between_time(stime,etime)])tmp_df = tmp_df.replace([np.inf, -np.inf], np.nan)tmp_df = tmp_df.dropna()return tmp_df['sig_theo2_mid']# 因子2: 挂单深度
def sig_depth(data: pd.DataFrame, weight: float, normalize_window: int, stime: str, etime: str) ->pd.DataFrame:df = copy.deepcopy(data)df['sig_depth'] = 0.for i in range(1, 6):df['sig_depth_{}'.format(i)] = (df['Ask{}Volume'.format(i)]-df['Bid{}Volume'.format(i)])/(df['Ask{}Volume'.format(i)]+df['Bid{}Volume'.format(i)])df['sig_depth'] += weight**i * df['sig_depth_{}'.format(i)] df['depth_mean'] = df['sig_depth'].rolling(normalize_window, min_periods=1).mean()df['depth_std'] = df['sig_depth'].rolling(normalize_window, min_periods=1).std()df['sig_depth'] = (df['sig_depth']-df['depth_mean'])/df['depth_std']df = df.replace([np.inf, -np.inf], np.nan)df = df.dropna()df = pd.concat([df.between_time(stime, etime)])df = df['sig_depth']return df"""计算因子值"""
factor1 = sig_theo2_price(data, 0.5, '09:35:00','14:55:00')
factor2 = sig_depth(data, 0.5, 5, '09:35:00','14:55:00')
print(factor1)
print(factor2) 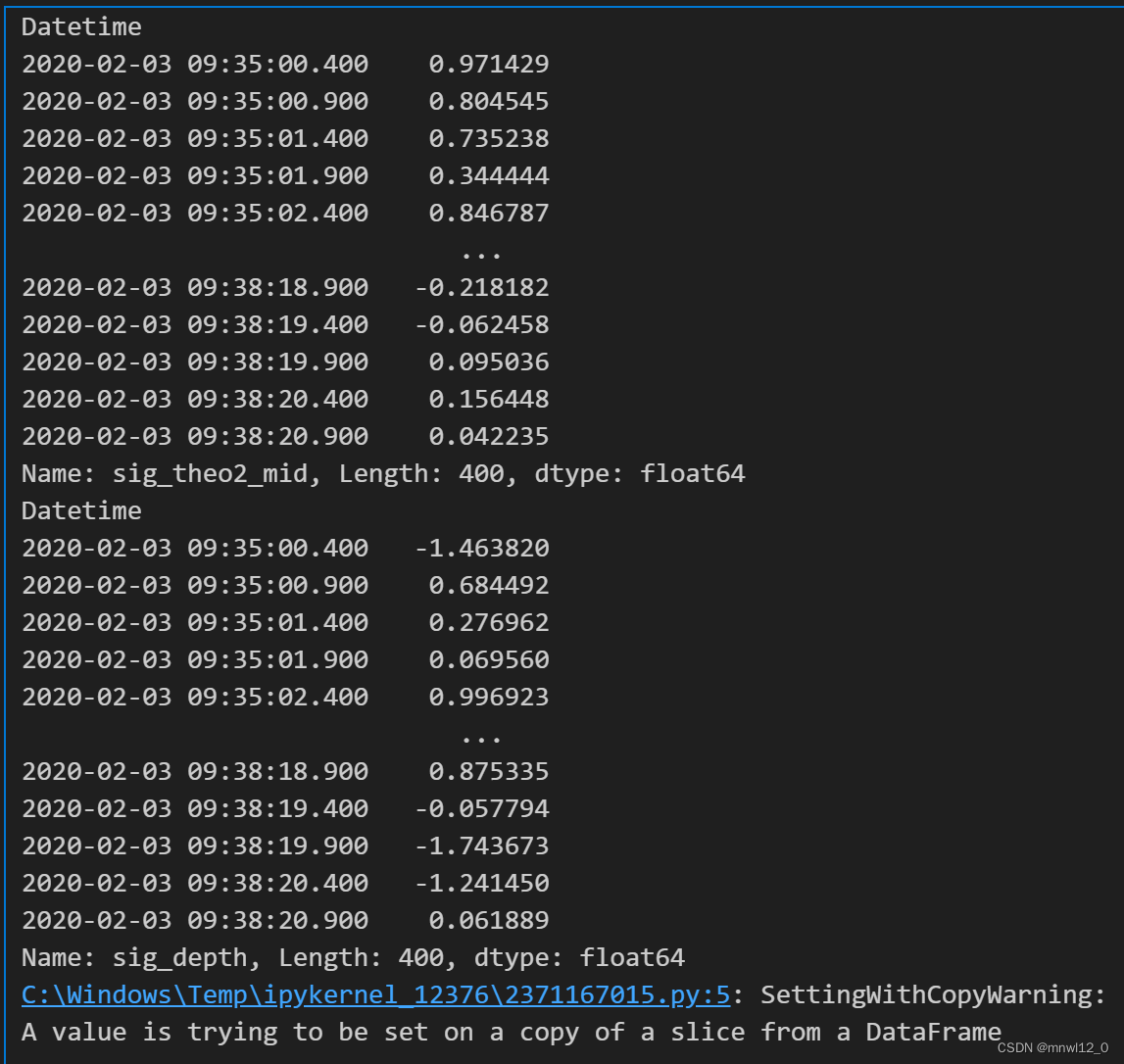
"""
对因子值画图,进行简单分析和数值调整
"""plt.plot(factor1)
plt.plot(factor2) 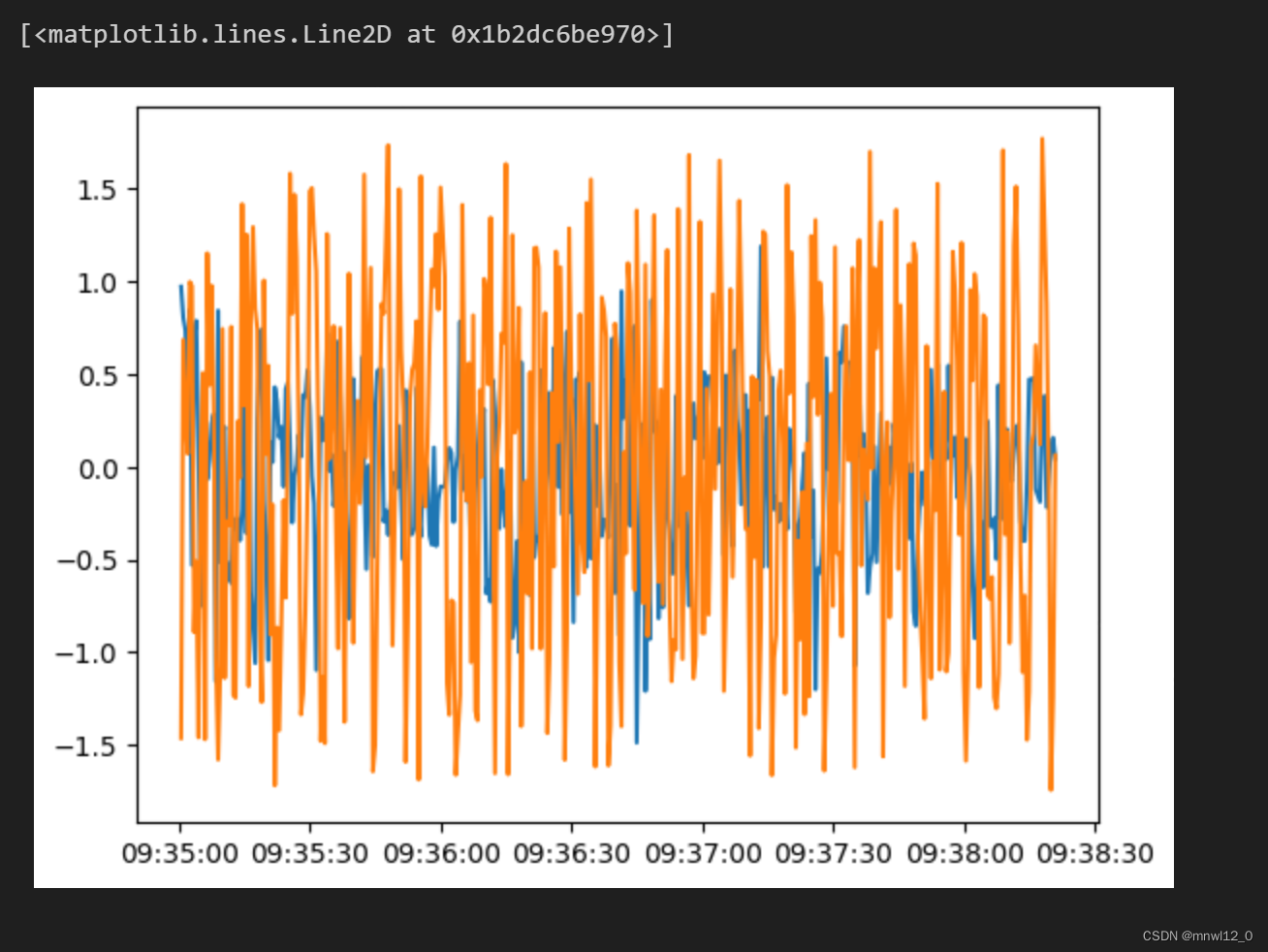
# 因子波动较大,存在大量噪声
# 可以参考置信区间的计算方法,设定临界值# 设置滚动窗口大小
window_size = 10# 计算滚动窗口的均值和标准差
rolling_mean = factor1.rolling(window=window_size, min_periods=1).mean()
rolling_std = factor1.rolling(window=window_size, min_periods=1).std()# 计算置信区间上下界(假设置信水平为95%)
confidence_interval = 1.96 * rolling_std # 1.96是95%置信水平对应的Z-score# 根据置信区间限制波动范围
upper_limit = rolling_mean + confidence_interval
lower_limit = rolling_mean - confidence_interval# 超出置信区间的波动直接取为临界值
price_diff_clipped = factor1.clip(upper=upper_limit, lower=lower_limit)# 绘制原始数据和置信区间
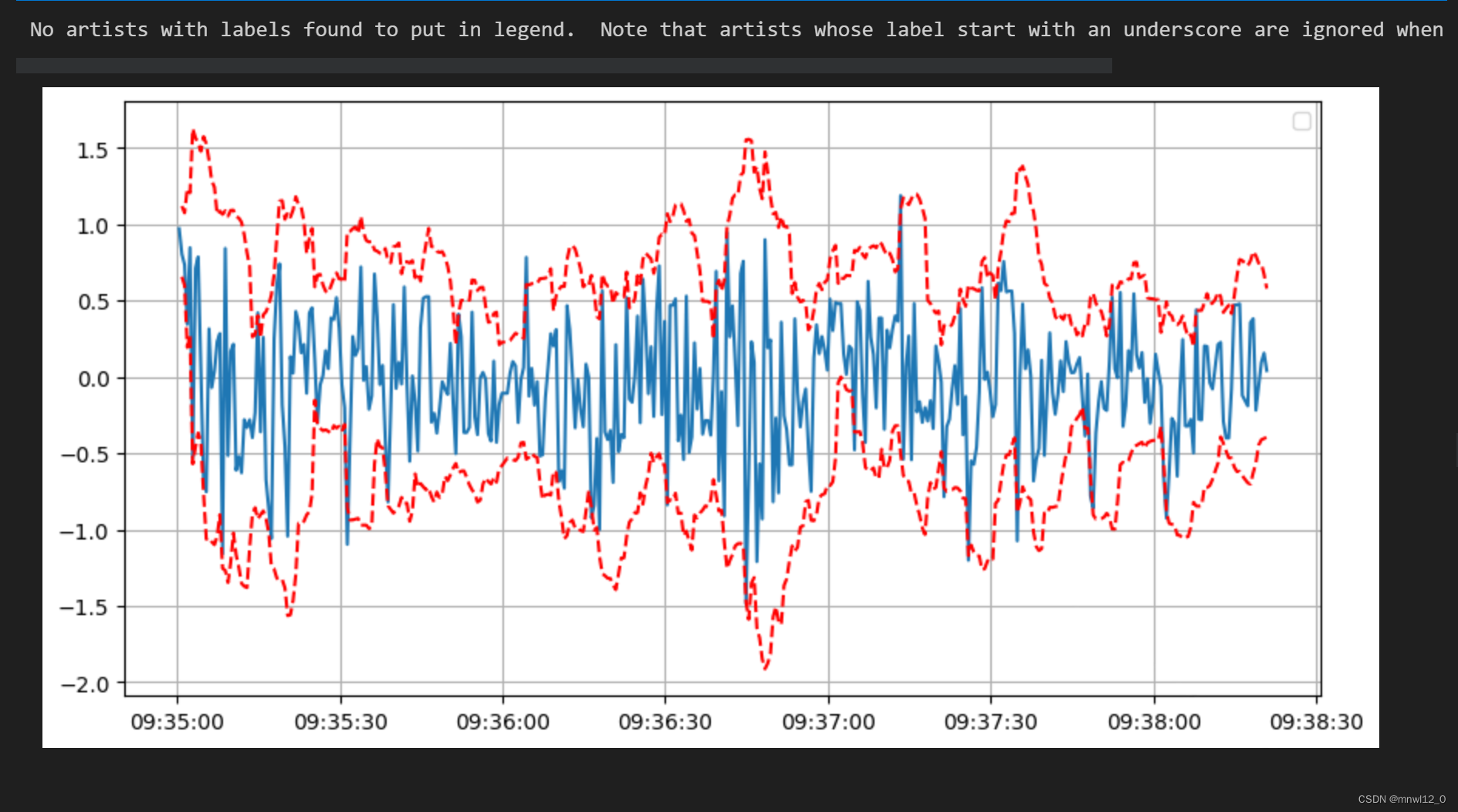
plt.figure(figsize=(10, 5))
plt.plot(factor1)
plt.plot(upper_limit, 'r--')
plt.plot(lower_limit, 'r--')
plt.legend()
plt.grid(True)
plt.show()
# 设置滚动窗口大小
window_size = 10# 计算滚动窗口的均值和标准差
rolling_mean = factor2.rolling(window=window_size, min_periods=1).mean()
rolling_std = factor2.rolling(window=window_size, min_periods=1).std()# 计算置信区间上下界(假设置信水平为95%)
confidence_interval = 1.96 * rolling_std # 1.96是95%置信水平对应的Z-score# 根据置信区间限制波动范围
upper_limit = rolling_mean + confidence_interval
lower_limit = rolling_mean - confidence_interval# 超出置信区间的波动直接取为临界值
volume_depth_clipped = factor2.clip(upper=upper_limit, lower=lower_limit)plt.plot(factor2) 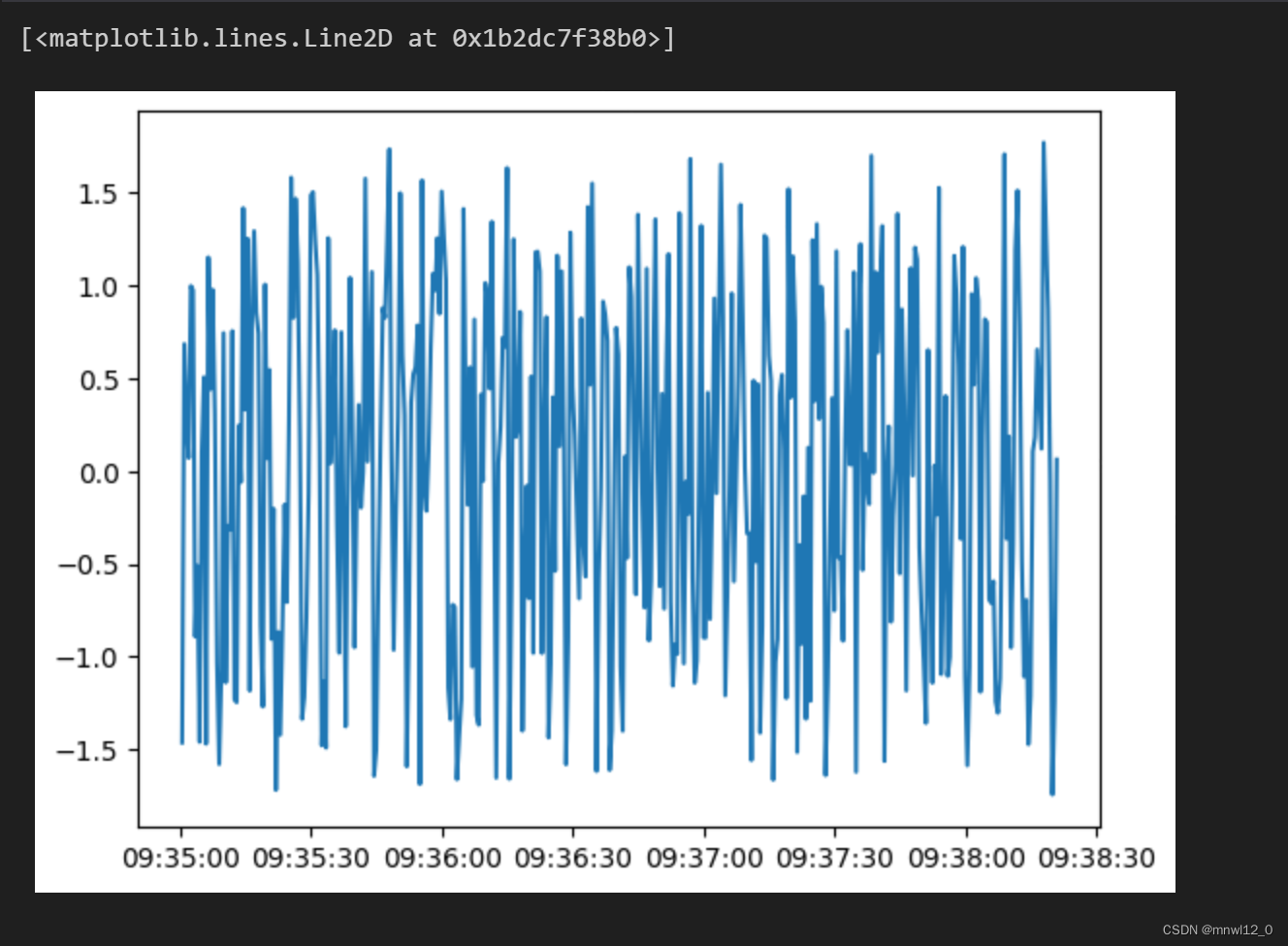
"""将因子值与预测值组合成一个dataframe"""
two_factors = pd.concat([factor1,factor2], axis=1)target_time = pd.Timestamp('2020-02-03 09:35:00.400')
# 使用loc属性选择满足条件的数据
selected_data = RET_Index.loc[RET_Index.index >= target_time]
# 打印大于2020-02-03 09:35:00.400的数据
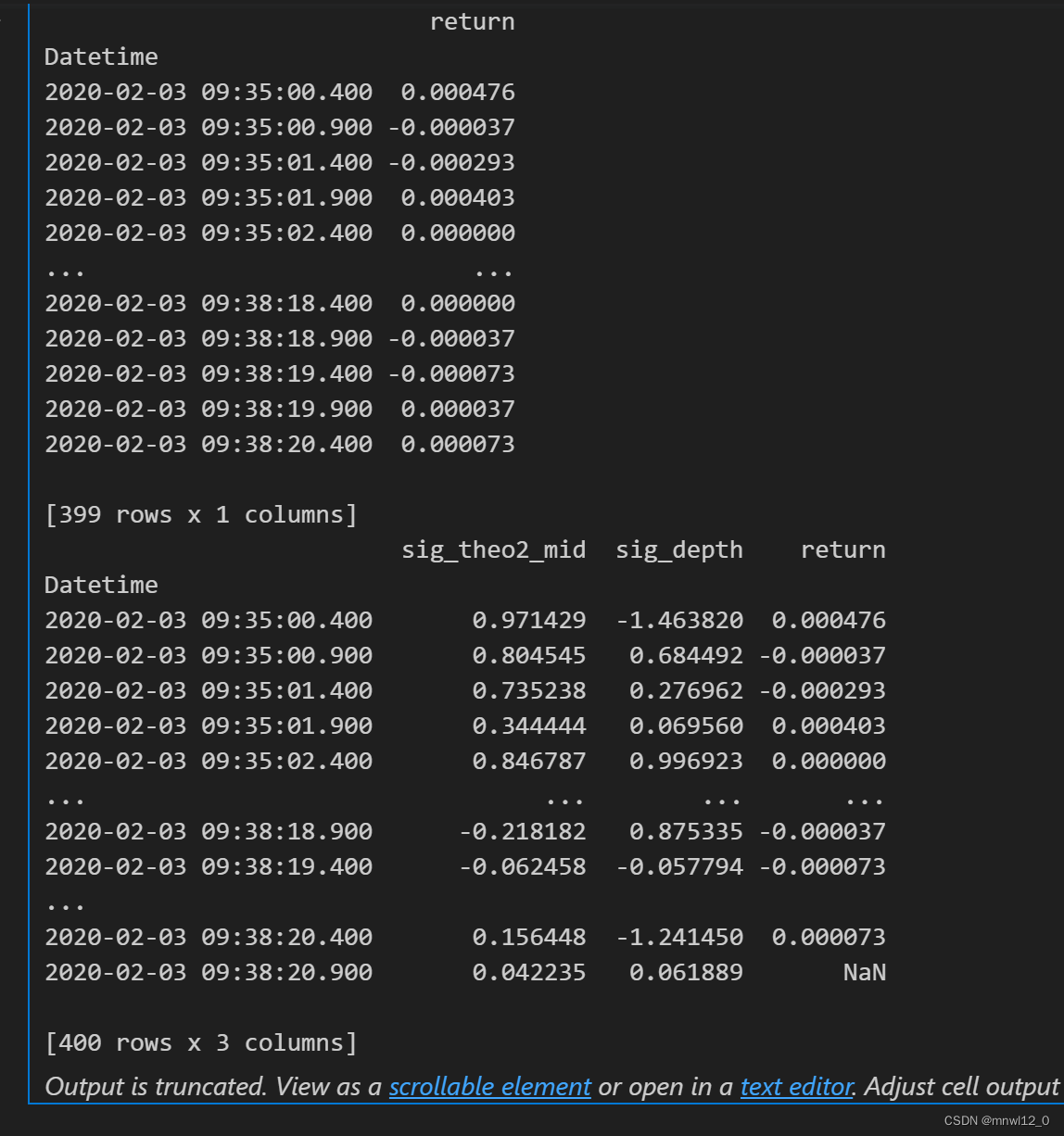
print(selected_data)combined_data = pd.concat([two_factors, selected_data], axis=1)
# 打印合并后的DataFrame
print(combined_data)
"""
单因子相关性分析
"""
corr_matrix = combined_data.corr()
corr_matrix 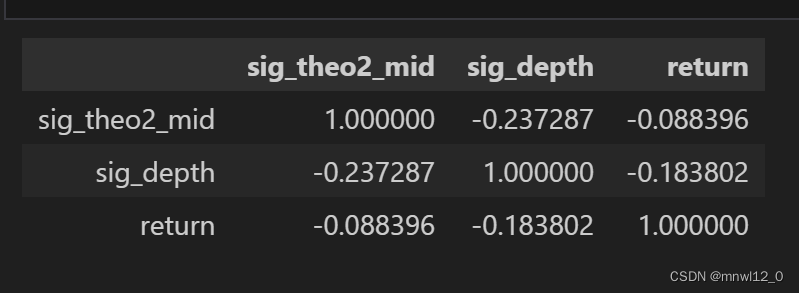
"""
因子数值稳定性(换手率和交易成本问题)结论,以及该怎么改进?
"""
# 计算因子sig_theo2_mid的均值和方差
mean_sig_theo2_mid = combined_data['sig_theo2_mid'].mean()
variance_sig_theo2_mid = combined_data['sig_theo2_mid'].var()# 计算因子sig_depth的均值和方差
mean_sig_depth = combined_data['sig_depth'].mean()
variance_sig_depth = combined_data['sig_depth'].var()variance_sig_depth# 因子sig_theo2_mid的数值稳定性相对sig_depth较好 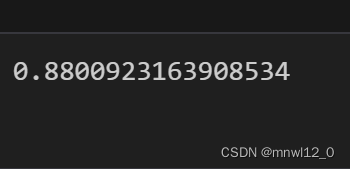
combined_data.isnull().sum()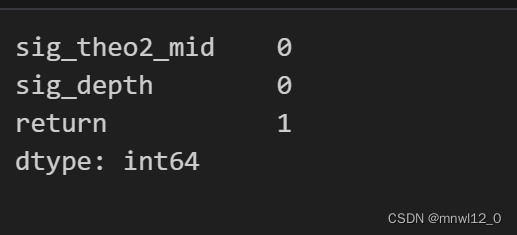
combined_data = combined_data.dropna()"""执行OLS拟合"""
combined_data.dtypesX = combined_data[['sig_theo2_mid', 'sig_depth']]
y = combined_data['return']# X = sm.add_constant(X)# 使用OLS类拟合线性模型
model = sm.OLS(y, X).fit()
# 打印模型摘要
print(model.summary())

"""
模型评估:线性模型的评估都包括哪些方面
"""
# MSE、MAE
from sklearn.metrics import mean_squared_error, mean_absolute_errormse = mean_squared_error(combined_data['return'], model.predict(X))
mae = mean_absolute_error(combined_data['return'], model.predict(X))print(mse)
print(mae)f_statistic = model.fvalue
f_statistic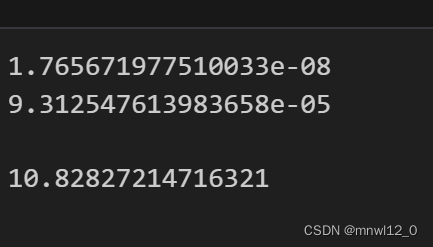
# 残差分析
residuals = combined_data['return'] - model.predict(X)plt.scatter(model.predict(X), residuals) 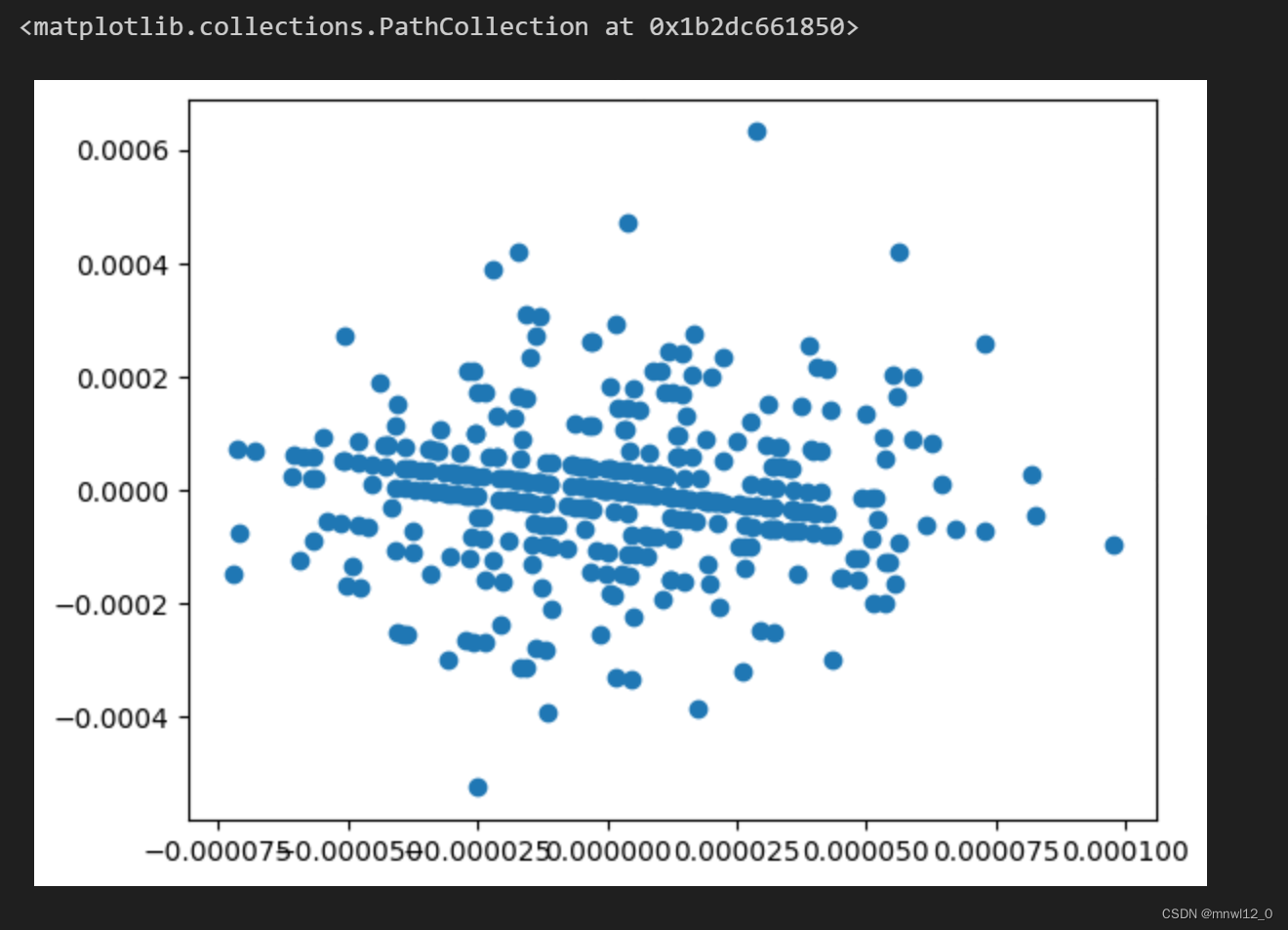
"""
思考两个问题:
1. 我们上述的线性模型中,有考虑截距吗?为什么?
2. 我们上述的模型评估使用了什么数据?这个结果完善了吗?
"""
#将样本切割为训练集和测试集,该模型在测试集上表现如何?
import pandas as pd
import statsmodels.api as sm
from sklearn.model_selection import train_test_split# 将自变量和因变量拆分出来
X = combined_data[['sig_theo2_mid', 'sig_depth']]
y = combined_data['return']# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 使用OLS类拟合线性模型
model = sm.OLS(y_train, X_train).fit()# 打印模型摘要
print(model.summary())
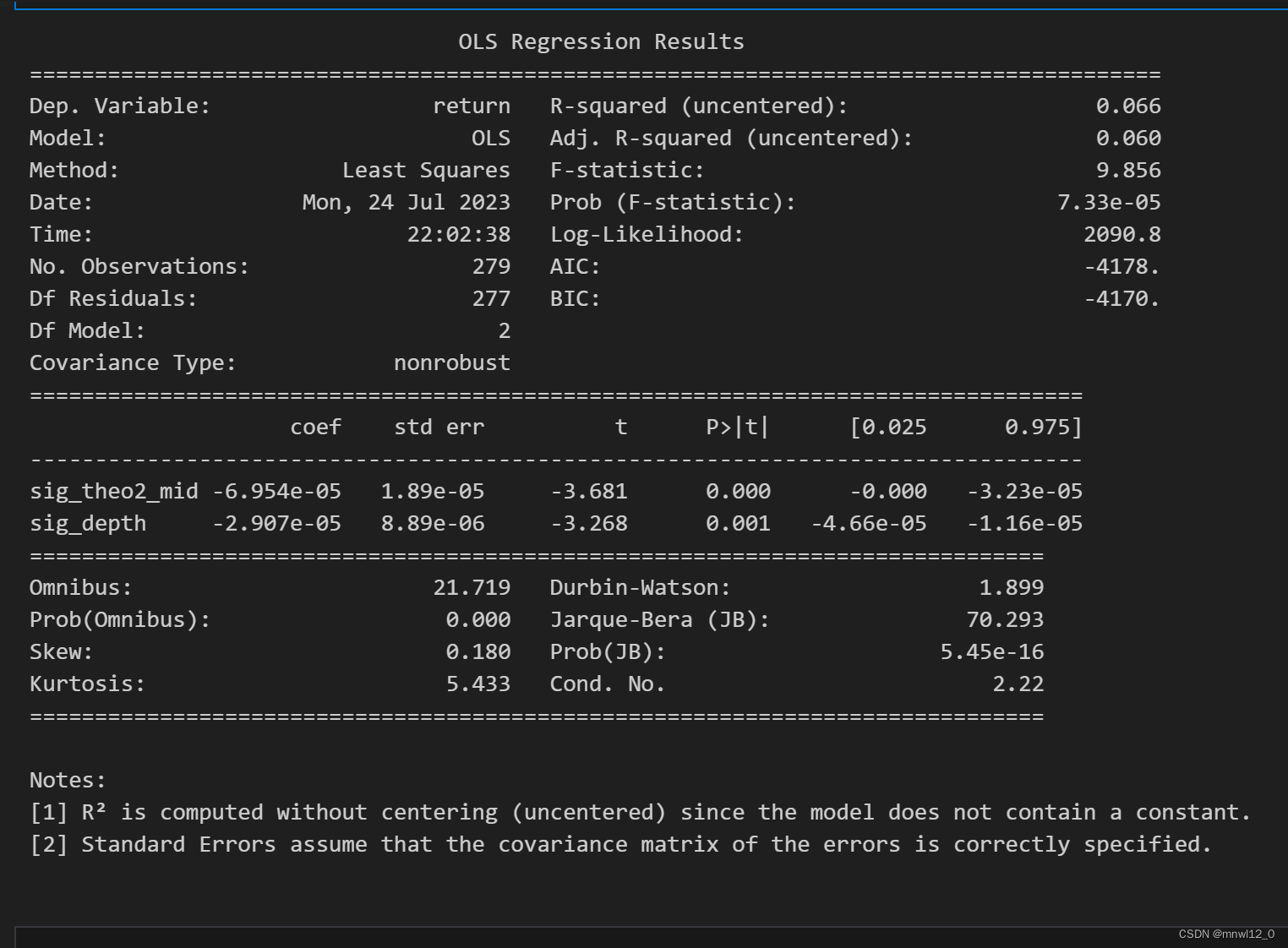
# 评估模型在测试集上的表现
# 可以计算MSE、MAE、R-squared等评估指标,以及绘制残差图等
# 例如:
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score# 在测试集上进行预测
y_pred_test = model.predict(X_test)mse_test = mean_squared_error(y_test, y_pred_test)
mae_test = mean_absolute_error(y_test, y_pred_test)
r_squared_test = r2_score(y_test, y_pred_test)
print("MSE on test set:", mse_test)
print("MAE on test set:", mae_test)
print("R-squared on test set:", r_squared_test)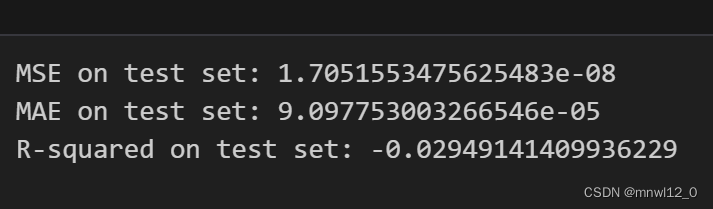
这篇关于#7.21研究目标:预测510050股指期货未来收益率的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








