本文主要是介绍Board,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
总结
这次诸事不顺和这题有点关系,(主要还是我太菜)
解决方法想出来了, 例题过了, 上交WA
后来发现算法有漏洞, 而且是本质性的。
改了很久 什么风车型 什么奇偶性 在上手之前都有找到了反例
最后想了一小时,放弃了,转向严晨晨的B题。
事后分析: 解决方法想出来后先证明, 实在不能证明就想反例。
* 除非即将结束才能冒死试试,不然刚开始就当头一棒, 这士气………………
上题
时间限制: 1 Sec 内存限制: 128 MB 提交: 68 解决: 8 [提交][状态][讨论版] 题目描述
There is a square of n*n.You need to cover the square with some small rectangle of k*1.How much can it cover at most?输入
There are multiple test cases in the input file.
First line contain the number of cases T (T≤10000).
In the next T lines contain T cases , Each case has two integers n and k. (1≤n,k≤100)输出
Print the maximum number of chessboard squares tiled.样例输入 2 6 3 5 3 样例输出 36 24 提示 来源 piaocoder
翻译
一个n * n 的正方形, 用 k * 1的矩形覆盖
小矩形不能超出大的正方形
问最后大正方形能被小矩形覆盖的最大面积
分析
详见原题分析
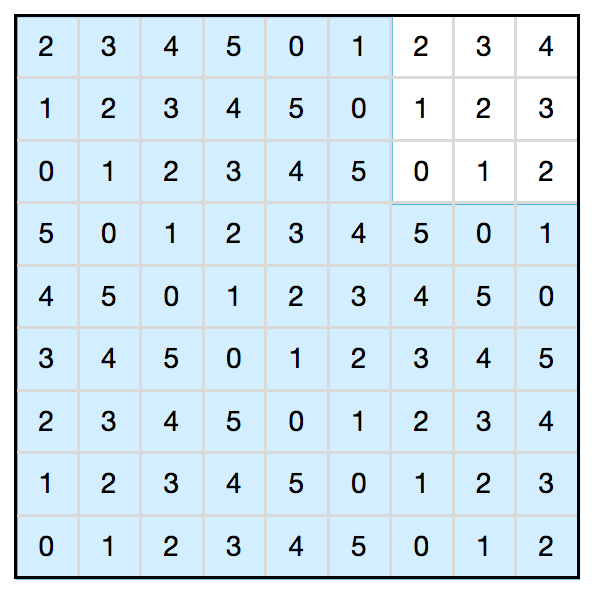
首先,若n < k,则棋盘连一个1×k的矩形都放不下,输出0。
·
我们只需要考虑n≥k的情况。将棋盘类似于黑白染色,
按(i+j)模k划分等价类,给每个格子标一个号。
标号之后,会注意到每条从左下到右上的斜线数字都是相同的,
那么对于s×s的格子,其内部数字有且恰好有2s−1种,
所以当s<=k2的时候,内部数字有floor(k2)∗2−1 < k种,所以不能有更佳的方案。
从而证明最优的方案一定是仅剩下一个s×s的正方形区域没有被覆盖到,其中s≤k2。
而令1 = n mod k之后,
根据l大小的不同,可以构造出中心为l×l或(k−l)×(k−l)的风车形图案,
又通过上面证明这个l(或k−l)就是之前的s,所以是最优的。
所以令1 = n mod k,如果l≤k2,最多可覆盖的格子数即为n2−l2,
否则为n2−(k−l)2,
显然这样的方案是可以构造出来的(风车形)。
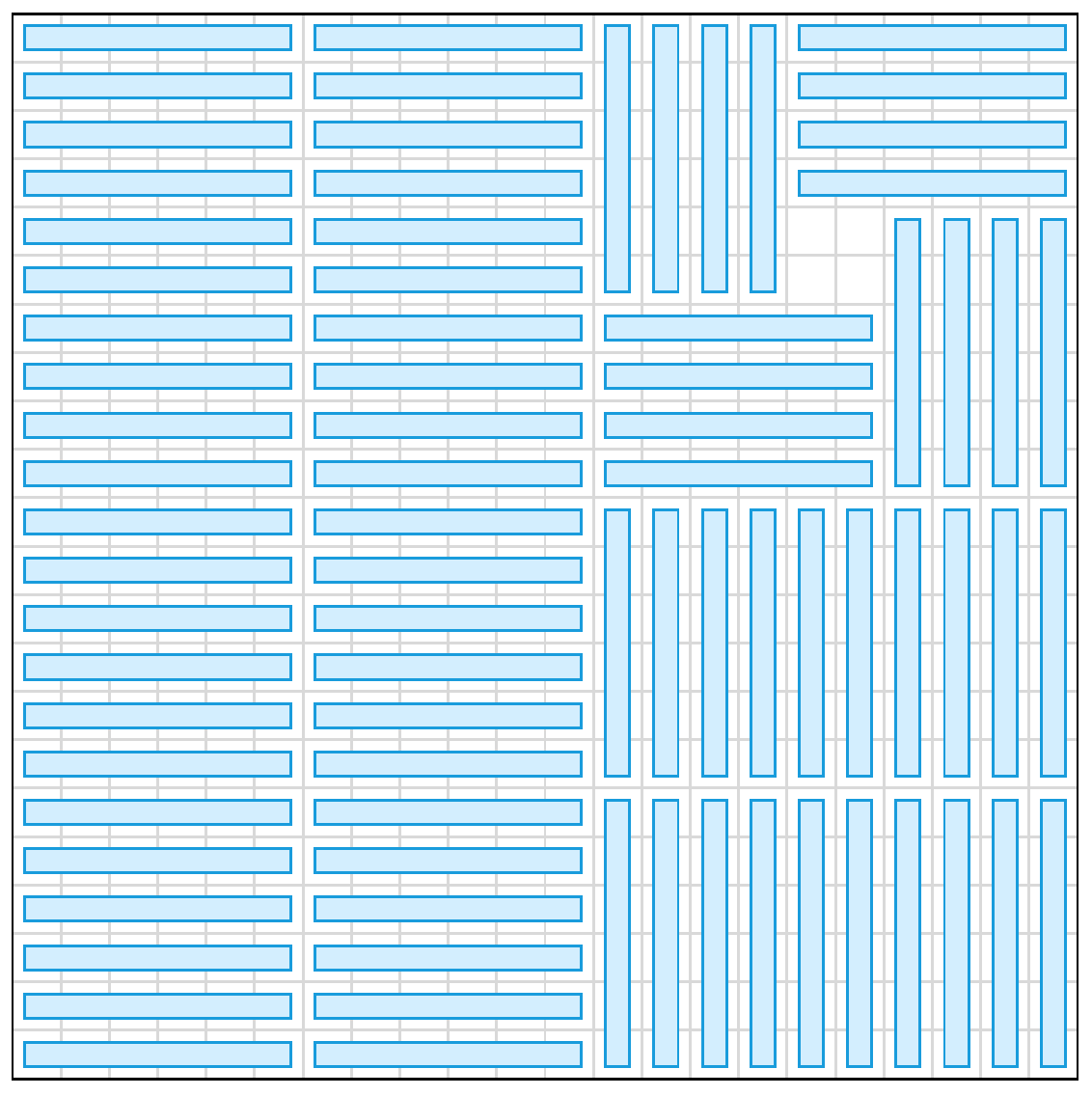
上代码
重点看分析 代码不贴
这篇关于Board的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!