工厂三姐妹——简单工厂模式

本文主要是介绍工厂三姐妹——简单工厂模式，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

概述

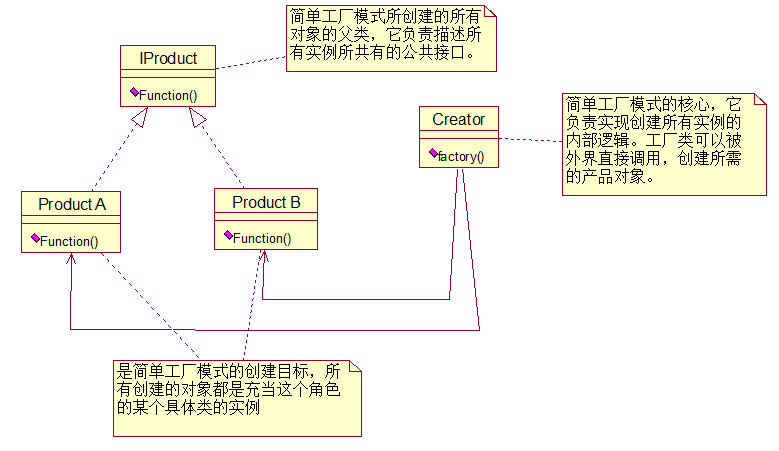
　　定义一个工厂类，它可以根据参数的不同返回不同类的实例，被创建的实例通常都具有共同的父类。因为在简单工厂模式中用于创建实例的方法是静态(static)方法，因此简单工厂模式又被称为静态工厂方法(Static Factory Method)模式，它属于类创建型模式。

　　简单工厂模式并不属于GoF 23个经典设计模式，原因是它违反了“开闭原则”，但通常将它作为学习其他工厂模式的基础，它的设计思想很简单，其基本流程如下：

　　首先将需要创建的各种不同对象的相关代码封装到不同的类中，这些类称为具体产品类，而将它们公共的代码进行抽象和提取后封装在一个抽象产品类中，每一个具体产品类都是抽象产品类的子类；然后提供一个工厂类用于创建各种产品。

　　简单工厂模式的核心是工厂类，在没有工厂类之前，客户端一般会使用new关键字来直接创建产品对象，而在引入工厂类之后，客户端可以通过工厂类来创建产品，在工厂类中提供一个创建产品的工厂方法，该方法可以根据所传入的参数不同创建不同的具体产品对象；客户端只需调用工厂类的工厂方法并传入相应的参数即可得到一个产品对象，职责分工见下图：

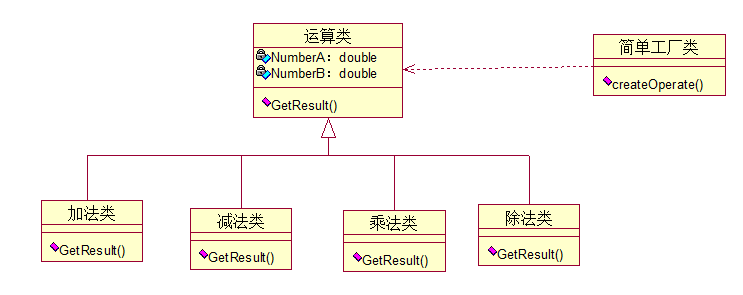
　　书中是用计算器作为实例讲解的，结构图如下：

代码展示

<span style="font-family:KaiTi_GB2312;">//简单运算工厂类
public class OperationFactory
{public static Operation createOperate(string operate){Operation oper = null;switch (operate){case "+":{oper = new OperationAdd();break;}case "-":{oper = new OperationSub();break;}case "*":{oper = new OperationMul();break;}case "/":{oper = new OperationDiv();break;}           }return oper;}
}</span>

<span style="font-family:KaiTi_GB2312;">// 运算类  public class Operation{private double _numberA = 0;private double _numberB = 0;        // 数字A     public double NumberA{get{return _numberA;}set{_numberA = value;}}//数字B public double NumberB{get{return _numberB;}set{_numberB = value;}}// 得到运算结果   public virtual double GetResult(){double result = 0;return result;}}
</span>

<span style="font-family:KaiTi_GB2312;">//加减乘除运算类// 加法类    class OperationAdd : Operation{public override double GetResult(){double result = 0;result = NumberA + NumberB;return result;}}    // 减法类和乘法类类似，此处省略// 除法类class OperationDiv : Operation{public override double GetResult(){double result = 0;if (NumberB == 0)throw new Exception("除数不能为0。");result = NumberA / NumberB;return result;}}</span>

结合代码看图说话

　　上图中，运算类就是所有实例（加减乘除等）的公用接口，简单工厂类中集合了所有的判断逻辑，它封装好的类必须是事先考虑好的，正因为如此，它违背了开闭原则。

　　简单工厂模式的要点在于：当你需要什么，只需要传入一个正确的参数，就可以获取你所需要的对象，而无须知道其创建细节。只要我们提出自己想要的运算，工厂就实例化出相应的对象，通过多态，返回父类的方法返回我们想要的计算结果。

小结　　

　　简单工厂模式的主要优点如下：

　　(1) 工厂类包含必要的判断逻辑，可以决定在什么时候创建哪一个产品类的实例，客户端可以免除直接创建产品对象的职责，而仅仅“消费”产品，简单工厂模式实现了对象创建和使用的分离。
　　(2) 客户端无须知道所创建的具体产品类的类名，只需要知道具体产品类所对应的参数即可，对于一些复杂的类名，通过简单工厂模式可以在一定程度减少使用者的记忆量。
　　(3) 通过引入配置文件，可以在不修改任何客户端代码的情况下更换和增加新的具体产品类，在一定程度上提高了系统的灵活性。

　　简单工厂模式的主要缺点如下：

　　(1) 由于工厂类集中了所有产品的创建逻辑，职责过重，一旦不能正常工作，整个系统都要受到影响。
　　(2) 使用简单工厂模式势必会增加系统中类的个数（引入了新的工厂类），增加了系统的复杂度和理解难度。
　　(3) 系统扩展困难，一旦添加新产品就不得不修改工厂逻辑，在产品类型较多时，有可能造成工厂逻辑过于复杂，不利于系统的扩展和维护。
　　(4) 简单工厂模式由于使用了静态工厂方法，造成工厂角色无法形成基于继承的等级结构。

　　适用场景:

　　(1) 工厂类负责创建的对象比较少，由于创建的对象较少，不会造成工厂方法中的业务逻辑太过复杂。
　　(2) 客户端只知道传入工厂类的参数，对于如何创建对象并不关心。