本文主要是介绍漫漫数学之旅018,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

文章目录
- 经典格言
- 数学习题
- 古今评注
- 名人小传 - 库尔特·哥德尔
经典格言
一个毫无自由的社会——一个人凡事都要遵循严格统一的规则——将在行为上既不一致也不完全,甚至不能解决某些也许很重要的问题。——库尔特·哥德尔(Kurt Gödel)
库尔特·哥德尔,这位逻辑界的“小淘气”,他要是来点评一个毫无自由的社会,那场景就像是他在给一部过于死板的数学剧本挑刺儿。想象一下,他说:“嘿伙计们,试想这么个地方:人们像机器人一样遵循着统一编程,一举一动都得按照刻板规则来,连上厕所都得严格按照规定的步数和节奏来完成。”
在这个社会里,每个人都像是精准到毫秒的钟表零件,各司其职,绝不越界半步。但问题是,这样的世界就像是一部永远无法自我修复的老旧机器,一旦遇到点儿意料之外的小插曲——比如,突然想要换个姿势喝咖啡或者心血来潮跳支舞,整个系统就有可能崩溃。
哥德尔会打趣说:“你们知道吗?这就好比是设计了一个超级严密的数学公式,本以为它能解决一切问题,结果呢,恰恰是那些不按常理出牌的‘变量’,也就是人的自由意志和创新行为,被无情地排除在外了。所以啊,这个看似完美的系统在面对生活中的实际挑战时,就像是一只抓不到自己尾巴的猫,既做不出灵活多变的动作,也解答不了生活中真正重要的那些‘谜题’。”
简单来说,哥德尔就是在用他的逻辑智慧告诉我们:如果一个社会把自由限制得太紧,那么这个社会的行为就会变得僵化而低效,甚至可能对一些关乎生存和发展的重要问题束手无策。这不仅缺乏生活的趣味性和多样性,而且从长远看,这样的社会难以应对复杂多变的世界所带来的挑战。
数学习题
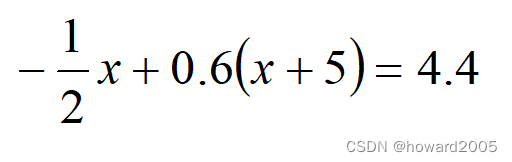
古今评注
在遥远的古代,当人们还在用石头刻字、兽皮记事的时代,计量单位就如同那个时代的语言一样,五花八门、各自为政。然而,智慧的埃及人率先做出了一个令人拍案叫绝的举动——他们如同打造神祇的信物一般,精心铸造了两种神秘的金属条。这可不是普通的铁棍或铜棒,而是蕴含着高度精确度量魔法的神器:长的一根对应着20.59英寸(这个长度让人不禁想起古埃及法老的权杖,其威严与精准并存),短的一根则象征着17.72英寸(就像王后用来测量宝石的皇家标尺)。这两个数字虽然看似平常,却开启了标准化计量的新纪元。
与此同时,在罗马帝国那片广袤的土地上,立法者们挥舞着手中的法律之剑,宣布了一项对人类文明产生深远影响的规定:罗马人民必须统一使用罗马单位,这是历史上首次大规模地对度量衡进行规范化。那些英勇无畏的罗马斗士和精明干练的市场商人,都得遵循这套以“十二”为尊的神圣体系。你瞧,“磅”(libra)这个词就承载着这样的历史痕迹,它是重量的权威代表,至今在英语中仍简写为lb,那是从拉丁文libra借来的,因为一libra恰好是罗马秤盘上的基本单位。
而在罗马人的生活画卷中,长度单位同样充满了生动有趣的细节。比如,五只脚丫子排成一行,那就是一步的距离;如果你有耐心连续走个一千步,恭喜你,你已经丈量出了一英里的宽度!这种把复杂的生活琐事转化为简单易记的数学关系的方式,既体现了罗马人的实用主义精神,又不失幽默风趣。
时光流转至现代社会,我们不再依赖于皇帝的谕令或是商人们的默契来决定一颗樱桃重多少、一条道路有多长。如今,科学的大旗高高飘扬,国际标准组织依据严谨的研究成果制定了全球通用的国际单位制,千克、米这些现代单位如同精密仪器般为我们的生活保驾护航。不过回望过去,我们依然会感慨那些古老的标准设立者们的聪明才智,他们的努力让世界在混乱中找到了秩序,也让后来的人们在讲述这段故事时忍不住会心一笑。
名人小传 - 库尔特·哥德尔

库尔特·哥德尔,这位大名鼎鼎的数学与逻辑学家,要是穿越到现代社交圈,大概会是那种朋友圈里让人既敬畏又捧腹的存在。想象一下,他带着一副深度近视眼镜,镜片后闪烁着智慧的光芒,宛如一位随时能揭示宇宙终极秘密的超级英雄“悖论侠”。他的头衔可能不是“哥德尔教授”,而是“无解先生”或“逻辑界的搅局者”。
哥德尔出生于1906年,奥地利小城布尔诺的一个普通家庭。小时候的哥德尔如果参加学校才艺表演,或许他会表演一个魔术:“看哪,我能让任何数学命题变得不确定!”——这当然预示了他后来提出的不完备性定理。
在学术界,哥德尔以其颠覆性的理论闻名遐迩。有一天,他站在一群顶尖数学家面前,就像马戏团的小丑突然扔出一颗震撼全场的炸弹,宣布了两个石破天惊的结论:一是任何形式化系统中总存在无法在该系统内部证明的真命题(第一不完备性定理);二是无法在同样的系统内证明自身的无矛盾性(第二不完备性定理)。这个声明就好比说,“瞧瞧你们这些自以为严谨的数学体系吧,就算你们再怎么严丝合缝,我也能找到你们的漏洞和自相矛盾之处!”
于是乎,哥德尔就这样凭借其独特的幽默感(尽管他是无比严肃的),让整个数学界陷入了集体挠头的境地,同时也赢得了众多敬仰的目光。他的工作不仅挑战了希尔伯特等人试图构建完备且一致的数学体系的梦想,也让世人对真理和知识的本质有了更深的认识。
如果哥德尔有社交媒体账号,他的签名档可能是:“证明了一切皆有可能被证明是错误的,但我对自己的天才却是无比确定。”这就是库尔特·哥德尔,一个用严密逻辑带给世界无限惊喜,同时又带有一丝幽默气质的大师级人物。
这篇关于漫漫数学之旅018的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






