本文主要是介绍Offer必备算法06_位运算_十道力扣OJ题详解_由易到难,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
位运算算法原理
①力扣191. 位1的个数
解析代码
②力扣338. 比特位计数
解析代码
③力扣461. 汉明距离
解析代码
④力扣136. 只出现一次的数字
解析代码
⑤力扣260. 只出现一次的数字 III
解析代码
⑥力扣面试题 01.01. 判定字符是否唯一
解析代码
⑦力扣268. 丢失的数字
解析代码
⑧力扣371. 两整数之和
解析代码
⑨力扣137. 只出现一次的数字 II
解析代码
⑩力扣面试题 17.19. 消失的两个数字
解析代码
本篇完。
位运算算法原理
常见位运算解题方法:
1. 基础位运算:
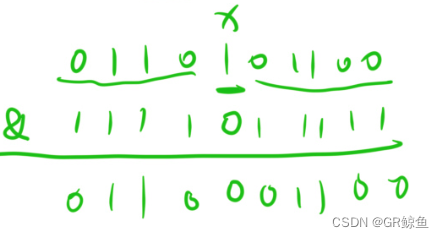
&:按位与,有0就是0
| :按位或,有1就是1
^ :按位异或,相同为0,相异为1/无进位相加
2. 给一个数 n,确定它的二进制表示中的第 x 位是 0 还是 1:
(n>>x)& 1 (n右移x位,按位与1)
为0则第x位为0,为1则第x位为1
3. 将一个数 n 的二进制表示的第 x 位修改成 1:
n l=(1<<x) (n或等 1左移x位)
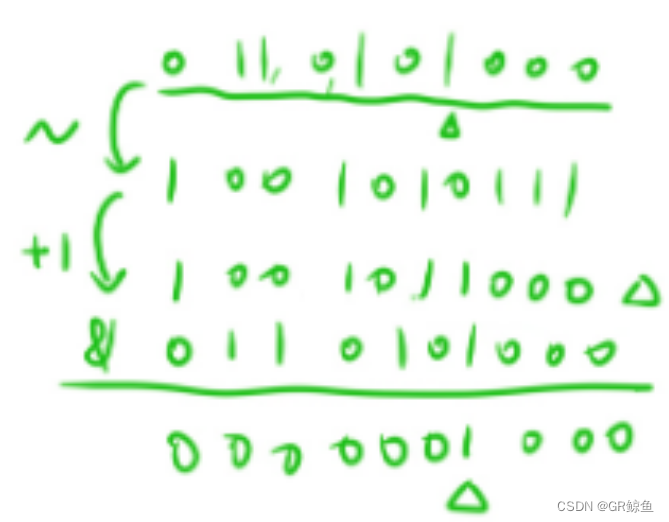
4. 将一个数 n 的二进制表示的第 x 位修改成 0:
n&=(~(1<<x)) (n与等 1左移x位然后按位取反)
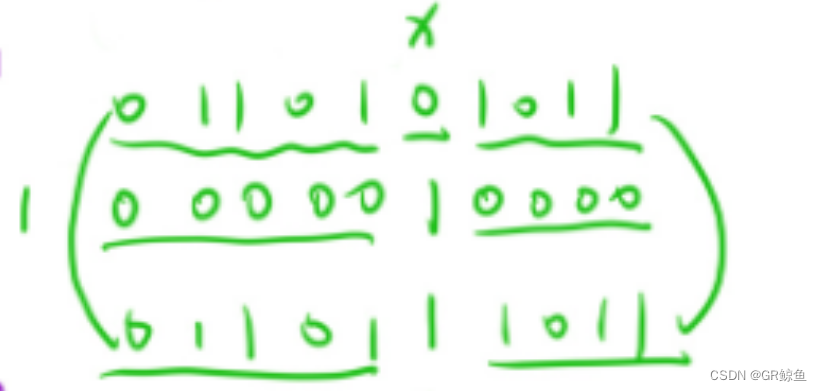
5. 提取一个数 n 二进制表示中最右侧的1:
n &-n(将最右侧的 1,左边的区域全部变成相反)
6. 干掉一个数 n 二进制表示中最右侧的 1(循环此方法知道n为0即可计算n二进制1的数目)
n & (n-1) (将最右侧的1,右边的区域(包含1)全部变成相反)
7. 异或(^)运算的运算律(解决只出现一次的数字(单身狗)问题)
a ^ 0 = a
a ^ a = 0
a ^ b ^ c = a ^ ( b ^ c)
①力扣191. 位1的个数
191. 位1的个数
难度 简单
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为汉明重量)。
提示:
- 请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
- 在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在 示例 3 中,输入表示有符号整数
-3。
示例 1:
输入:n = 00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 00000000000000000000000010000000 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 11111111111111111111111111111101 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
- 输入必须是长度为
32的 二进制串
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
class Solution {
public:int hammingWeight(uint32_t n) {}
};解析代码
干掉最右边的1,然后计数器+1:
class Solution {
public:int hammingWeight(uint32_t n) {int cnt = 0;while(n){n &= (n - 1);++cnt;}return cnt;}
};②力扣338. 比特位计数
338. 比特位计数
难度 简单
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2 输出:[0,1,1] 解释: 0 --> 0 1 --> 1 2 --> 10
示例 2:
输入:n = 5 输出:[0,1,1,2,1,2] 解释: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101
提示:
0 <= n <= 10^5
class Solution {
public:vector<int> countBits(int n) {}
};解析代码
只是(力扣191. 位1的个数)加了个循环:
class Solution {
public:vector<int> countBits(int n) {vector<int> v(n+1, 0);for(int i = 1; i <= n; ++i){int cnt = 0, tmp = i;while(tmp){tmp &= (tmp - 1);++cnt;}v[i] = cnt;}return v;}
};③力扣461. 汉明距离
461. 汉明距离
难度 简单
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4 输出:2 解释: 1 (0 0 0 1) 4 (0 1 0 0)↑ ↑ 上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1 输出:1
提示:
0 <= x, y <= 2^31 - 1
class Solution {
public:int hammingDistance(int x, int y) {}
};解析代码
把两个数异或起来,计算其结果二进制1的数目:
class Solution {
public:int hammingDistance(int x, int y) {// return __builtin_popcount(x ^ y);int tmp = x ^ y, cnt = 0; // 不同则为1while (tmp) {tmp &= (tmp - 1);++cnt; // 依次左移到最低位}return cnt;}
};④力扣136. 只出现一次的数字
136. 只出现一次的数字
难度 简单
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
提示:
1 <= nums.length <= 3 * 10^4-3 * 10^4 <= nums[i] <= 3 * 10^4- 除了某个元素只出现一次以外,其余每个元素均出现两次。
class Solution {
public:int singleNumber(vector<int>& nums) {}
};解析代码
之前写过了,以前讲异或讲过的单身狗:
class Solution {
public:int singleNumber(vector<int>& nums) {int val = 0;for(const auto& e : nums){val ^= e;}return val;}
};⑤力扣260. 只出现一次的数字 III
260. 只出现一次的数字 III
难度 中等
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0] 输出:[-1,0]
示例 3:
输入:nums = [0,1] 输出:[1,0]
提示:
2 <= nums.length <= 3 * 10^4-2^31 <= nums[i] <= 2^31 - 1- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {}
};解析代码
这也可以用排序,但这是以前写过的找两个单身狗的题:时间复杂度为O(N)
如果我们按照只出现一次的数字的思路直接异或 肯定只会出来一个四不像数,假设数组1 2 3 3 1 4,我们把 两个单身狗分成两个组。而组中其他的数字就都不是单身狗。
此时我们在分组异或就分别得到了2个单身狗,问题是以什么为依据分组?依据 二进制位 异或把相同的数字变成0,不同的数字变成1,根据1在哪位 就说明单身狗这个的二进制位不同 ,按照这个二进制位分(这就是那个四不像的数)两个单身狗是不可能进到一组的。
① 我们依然把数组中所有数字异或到一起 然后判断这个数字的二进制位 比如有两个单身狗2和40010 和0100最后异或完毕得到的二进制位是 0110 说明两个单身狗数字的二进制最后位是相等我们左移一(cnt)位得到了1 就说明 两个单身狗数字的倒数第二位二进制数 不相等
② 让数组中所有的数字左移一(cnt)位 如果等于 1 放进第一个数组中。如果等于0 放进第二个数组中。
③ 把数组中的数字全部异或就得到了 2个单身狗
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {int sum = 0;for (const auto& e : nums){sum ^= e;}int cnt = 0;for (int i = 0;i < 32;++i){if (sum & (1 << i))// 第几位是1结果就是1{cnt = i;// 记录下来}}vector<int> v = { 0,0 };// C++11的初始化,类似数组for (const auto& e : nums){if (e & (1 << cnt)){v[0] ^= e;}else{v[1] ^= e;}}return v;}
};⑥力扣面试题 01.01. 判定字符是否唯一
面试题 01.01. 判定字符是否唯一
难度 简单
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = "leetcode"
输出: false
示例 2:
输入: s = "abc"
输出: true
限制:
0 <= len(s) <= 100s[i]仅包含小写字母- 如果你不使用额外的数据结构,会很加分。
class Solution {
public:bool isUnique(string astr) {}
};解析代码
class Solution {
public:bool isUnique(string astr) {if(astr.size() > 26) // 鸽巢原理优化return false;int bits = 0;for(auto& e : astr){int i = e - 'a';if((bits >> i) & 1){return false;}bits |= (1 << i);}return true;}
};⑦力扣268. 丢失的数字
268. 丢失的数字
难度 简单
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1] 输出:2 解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1] 输出:8 解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0] 输出:1 解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length1 <= n <= 10^40 <= nums[i] <= nnums中的所有数字都 独一无二
class Solution {
public:int missingNumber(vector<int>& nums) {}
};解析代码
转化成找一个单身狗(力扣136):
class Solution {
public:int missingNumber(vector<int>& nums) {int ret = 0;for(auto& e: nums){ret ^= e;}for(int i = 0; i <= nums.size(); ++i){ret ^= i;}return ret;}
};⑧力扣371. 两整数之和
371. 两整数之和
难度 简单
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2 输出:3
示例 2:
输入:a = 2, b = 3 输出:5
提示:
-1000 <= a, b <= 1000
class Solution {
public:int getSum(int a, int b) {}
};解析代码
此题知识点就是异或运算为无进位相加,异或后想办法找到进位就行了,进位就是两个数按位与然后左移一位,重复相加至进位为0即为答案。
class Solution {
public:int getSum(int a, int b) {while (b != 0){unsigned int carry = (unsigned int)(a & b) << 1; // 进位a = a ^ b; // 无进位相加b = carry; // 进位不为0的话就一直加,如a已经是a^b的结果,再^b,加进位}return a;}
};⑨力扣137. 只出现一次的数字 II
137. 只出现一次的数字 II
难度 中等
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2] 输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99] 输出:99
提示:
1 <= nums.length <= 3 * 10^4-2^31 <= nums[i] <= 2^31 - 1nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
class Solution {
public:int singleNumber(vector<int>& nums) {}
};解析代码
1. 基础位运算:
&:按位与,有0就是0
| :按位或,有1就是1
^ :按位异或,相同为0,相异为1/无进位相加
之前用暴力和sort写过了,现在再用位运算写一下,思路就是把全部数的二进制位加起来,模3(一个数出现一次,其它出现n次就是模n),因为如果不看只出现一次的数,其它二进制位加起来不是3n个0就是3n个1,那一位全加起来模3的话剩的就是只出现一次的数的二进制位。
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < 32; ++i) // 依次修改ret的32个比特位->0改1{int sum = 0;for(auto e : nums){// if(((e >> i) & 1) == 1)// {// ++sum; // 依次统计所有数的第i位二进制位// }sum += ((e >> i) & 1); // 即上面注释掉的代码简化,不是加0就是加1}if(sum %= 3) // 说明这是只出现一次的数剩的1{ret |= (1 << i); // ret第i位改为1}}return ret;}
};⑩力扣面试题 17.19. 消失的两个数字
面试题 17.19. 消失的两个数字
难度 困难
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O(N) 时间内只用 O(1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:
输入: [1]
输出: [2,3]
示例 2:
输入: [2,3]
输出: [1,4]
提示:
nums.length <= 30000
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {}
};解析代码
困难题,但之前写过找一个单身狗和找两个单身狗的了,转化成找两个单身狗(力扣260),再转化成找一个单身狗(力扣136)(力扣268):
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int sum = 0, n = nums.size();for(int i = 1; i <= n + 2; ++i){nums.push_back(i); // 转换成找两个单身狗->力扣260}n = nums.size();for (int i = 0; i < n; i++){sum ^= nums[i];}int count = 0;for (int i = 0; i < 32; i++){if (sum & 1 << i) //循环判断第几位是1{count = i;//如果是1 记录下来break;}}int a = 0, b = 0;for (int i = 0; i < n; i++){if (nums[i] & 1 << count)a ^= nums[i];elseb ^= nums[i];}return {a, b};}
};本篇完。
下一部分是关于递归的。
这篇关于Offer必备算法06_位运算_十道力扣OJ题详解_由易到难的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!