本文主要是介绍《算法图解》-第一天(20210129)-TinyBrushCoding,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《算法图解》——第一天(20210129)
文章目录
- 《算法图解》——第一天(20210129)
- 前言
- 第一章:算法简介
- 1.1 二分法
- 1.2 时间复杂度(大O表示法)
- 第二章:选择排序
- 2.1 链表
- 2.2 数组
- 2.3 链表与数组的时间复杂度对比
- 第三章:递归
- 3.1 递归
- 3.2 堆栈
前言
本文为算法学习随记,希望大家多多支持,如有错误,欢迎指正
第一章:算法简介
本章主要内容:
1.二分法
2.时间复杂度(大O表示法)
1.1 二分法
- 定义:(在找数程序中)将数据按照对半切分,在形成的两个数据集A,B中进行判断,若数据在A,则再从A中进行二分法。(反之亦然)
- 时间复杂度:O( l o g n log n logn)
1.2 时间复杂度(大O表示法)
-
定义:定性描述一个算法的运行时间。
-
表示方式(大O表示法):T(n) = O( )
-
常见的时间复杂度:
时间复杂度 O表达式 代表算法 常数时间 O( 1 1 1) 直接输出 对数时间 O( l o g n log n logn) 二分法查找 线性时间 O( n n n) 遍历和扫描 线性对数时间 O( n ∗ l o g n n*log n n∗logn) 二分法、贪心算法 平方时间 O( n 2 n^2 n2) 枚举、动态规划 立方时间 O( n 3 n^3 n3) 动态规划 指数时间 O( 2 n 2^n 2n) 搜索 乘时间 O( n ! n! n!) 产生全排列 -
时间复杂度对比
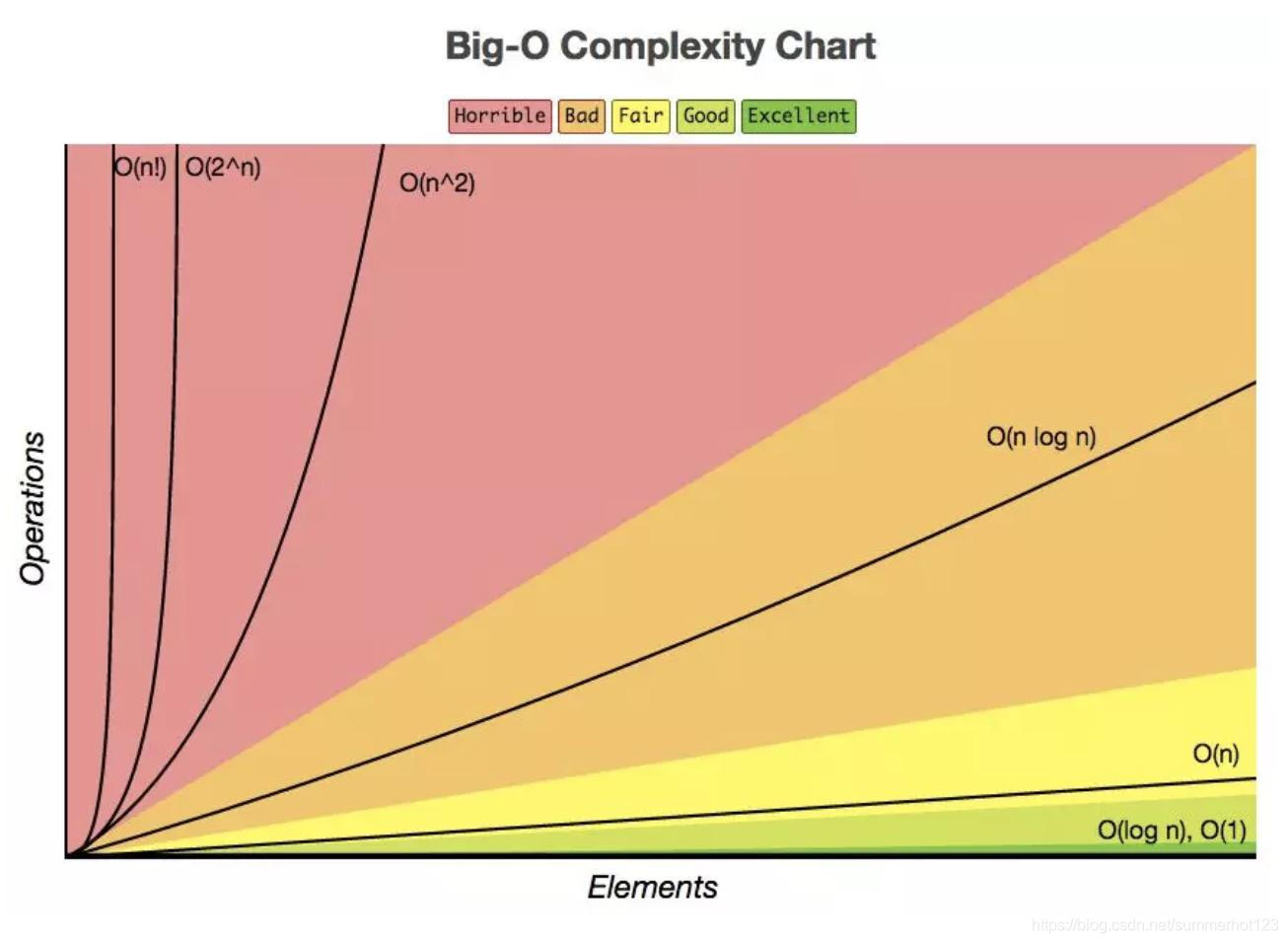
第二章:选择排序
本章主要内容:
1.链表
2.数组
2.1 链表
- 定义:链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。
- 组成:链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:1.存储数据元素的数据域;2.存储下一个结点地址的指针域。
- 优点:
- 占用内存少。不用数组单独开辟储存单元,对数据进行处理。
- 修改数据时间复杂度低。只需要更改需要修改存储单元前后的指针域即可。
- 缺点:只能进行顺序访问,只能按照链表顺序进行查询。
2.2 数组
- 定义:数组是一种物理存储单元上连续、顺序的存储结构。
- 优点:可以进行随机访问。只需要知道一个存储单元的物理地址就可计算出其他的存储单位的地址。
- 缺点:
- 浪费存储空间。对数据进行处理时,必须单独开辟一块存储区域进行数据处理,若未使用完存储区域则会浪费存储空间;若超出存储区域则无法进行超出的存储,若要进行数据处理,则需要重新开辟存储空间。
- 修改数据时间复杂度高。若增加/减少其中一个存储单元数据,则修改单元后面的数据全部都要进行处理。
2.3 链表与数组的时间复杂度对比
| 时间复杂度 | 数组 | 链表 |
|---|---|---|
| 读取 | O( 1 1 1) | O( n n n) |
| 插入 | O( n n n) | O( 1 1 1) |
| 删除 | O( n n n) | O( 1 1 1) |
第三章:递归
本章主要内容:
1.递归
2.堆栈
3.1 递归
- 定义:循环调用自身函数,每次循环会有新的输出和输入,直到循环结束。
- 适合用递归的三类问题:
- 数据的定义是按递归定义的。(如:Fibonacci函数)
- 数据的结构形式是按递归定义的。(如二叉树、广义表等,由于结构本身固有的递归特性,则它们的操作可递归地描述。)
- 问题解法按递归算法实现。(这类问题本身没有明显的递归结构,但用递归求解更简单,如Hanoi问题)
- 优点:大大减少了代码量,且可读性增强。
- 缺点:只能进行普通循环,其运行效率较低。
Code:
def fiboc(n):if n <= 2:return 1else:sum = fiboc(n - 2) + fiboc(n - 1)return sumfiboc(6)
Answer:
8
3.2 堆栈
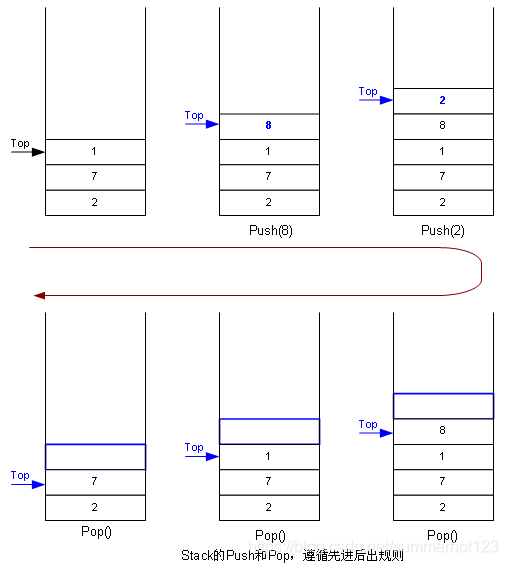
- 定义:堆栈是一个特定的存储区或寄存器,它的一端是固定的,另一端是浮动的。堆栈只能进行入栈与出栈操作,且只能对最上端的浮动端进行操作
- 堆栈与递归的联系:递归将执行语句压入堆栈中,最后再进行执行。
这篇关于《算法图解》-第一天(20210129)-TinyBrushCoding的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









