本文主要是介绍ACM 选手带你玩转哈希表!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
大家好呀,我是你们的 Rocky0429。
之前我在讲数组的时候说过:要查一个数在数组中的位置,那可是太费劲了,只能从头开始一个个的比较,直到找到相等的才算完事。
这个方法,说实话也太笨了,简直不是我这种懒人应该做的事。
就不能有种方法直接看到这个数,就直接在数组中查到位置嘛?!
诶,你别说,还真有。
因为总有比我更懒的,蛋蛋懒是只能躺着,人家大佬懒是直接动手解决,果然那句”懒是第一生产力“,诚不我欺!
这个就是我今天要给小婊贝们讲的:哈希表。
哈希表
哈希表,别名儿叫散列表,洋名儿叫 Hash Table。
我在上面讲,希望有种方法,直接看到数,就知道它在数组中的位置,其实里就用到了哈希思想。
哈希思想就是说不用一些无用的比较,直接可以通过关键字 key 就能找到它的存储位置。
我来举个场景,可能更清楚点:
狗蛋班有 40 个学生,每个学生的学号由入学年份 + 年级 + 班级 + 编号组成,例如 2021210129 是 2021 年入学的 21 级 01 班的 29 号同学。
现在有个需求:我们需要快速找到某个同学的个人信息。
那这个时候我们就要建立一张表,按理来说我要是想要知道某个同学的个人信息,其实就知道学号就好了,但是在这不行,学号的值实在太大了,我们不能把学号当作下标。
学号不可以,那啥可以?我们定睛一看,咦,编号可以呀,编号是从 1 ~ 40。
那咋取到编号?不就是学号对 2021210100 取余就 ok 了嘛。
此时,如果我们想查学号为 2021210129 的学生个人信息,只要访问下标为 29 的数据即可。
其实这就可以在时间复杂度为 O(1) 内解决找到。
秒男实锤。

用公式表示就是:存储位置 = f(关键字)。
这里的 f 又叫做哈希函数,每个 key 被对应到 0 ~ N-1 的范围内,并且放在合适的位置。
在上面的例子中 f(key) = key % 2021210100。
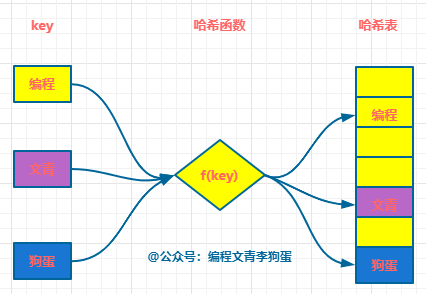
存储时,通过同一个哈希函数的计算 key 的哈希地址,并按照此哈希地址存储该 key。
最后形成的表就是哈希表,它主要是面向查找的存储结构,简化了比较的过程,提高了效率。

哈希示例
上面看明白的话,那再举个小例子加深点印象。
有个 n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列到数组中。
哈希函数确定后,剩下的就是计算关键字对应的存储位置。
1. 4 % 10 = 4,所以将 4 放入下标为 4 的位置。

2. 10 % 10 = 0,所以将 10 放入下标为 0 的位置。

3. 11 % 10 = 1,所以将 11 放入下标为 1 的位置。

4. 19 % 10 = 9,所以将 19 放入下标为 9 的位置。

5. 29 % 10 = 9,所以将 29 放入下标为 9 的位置。
但是现在问题来了,下标为 9 的这个坑已经被 19 占了,这 29 计算出来的下标冲突了。
这种情况有个学名,叫:哈希(散列)冲突。
处理哈希冲突
对于两个不相等的关键字 key1 和 key2,若 f(key1) = f(key2),这就是哈希冲突。
key1 占了坑,那 key2 只能想别的办法,啥办法呢?
一般处理哈希冲突有以下几种办法:
开放定址法
再哈希(散列)函数法
链地址法
。。。
开放定址法
开放定址法就是:一旦发生冲突,就选择另外一个可用的位置。
开放定址法有 2 个最常用的策略:
线性探测法
二次探测法
线性探测法
线性探测法,顾名思义,直来直去的探测。
且看它的公式:
f(key) = (f(key) + di) % m (di = 1, 2, 3, ... , m-1)。
我还是用“哈希示例”中的例子:
n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列到数组中。

到了 29 的时候,29 % 10 = 9。
但此时下标 9 已经有了元素 19,所以此时探测下一个位置 (9 + 1) % 10 = 0。
下标为 0 的位置上已经有了元素 10,所以继续探测下一个位置 (9 + 2) % 10 = 1。
下标为 1 的位置上也有了元素 11,所以还得继续探测下一个位置 (9 + 3) % 10 = 2。
下标为 2 的位置上总算是空的,因此 29 找到了家:

不知道你发现了没,对于 29 这个来说,本来只是和 19 冲突,整着整着和 10,11 也冲突了。
这样就使得每次要处理好几次冲突,而且这样会出现大量数字聚集在一个区域的情况,大大降低了插入和查找的效率。
后来不知道哪个大佬在线性的基础上做了改进,捣鼓出二次探测法。
二次探测法
二次探测法就是把之前的 di 整成了平方,公式如下:
f(key) = (f(key) + di) % m (di = 1², -1², 2², -2², ..., q², -q², q ≤ m/2)
比如对于 29 来说,下标为 9 的位置上呆了19,所以此时探测下一个位置 (9 + 1²) % 10 = 0。
下标为 0 的位置上占了元素 10,那下一次就探测上一个位置 (9 - 1²) % 10 = 8。
下标为 8 的位置上空着,直接占住:

再哈希(散列)函数法
再哈希的话,就是不只是一个哈希函数,而是使用一组哈希函数 f1(key)、f2(key)、f3(key)....。
当使用第一个哈希函数计算到的存储位置被占了,那就用第二个哈希函数计算,反正总会有一个散列函数能把冲突解决掉。
依次类推,直到找到空的位置,然后占住。
当然这种方法不会出现大量数字聚集在一个区域的情况,但这种情况明显增加了计算的时间。
链地址法
是谁说出现冲突后只能找别的坑位的,几个人蹲一个坑它不香嘛。

可能真的有巨佬觉得香,然后就整出了链地址法。
链地址法呢是将得出同一个结果的 key 放在一个单链表中,哈希表存储每条单链表的头指针。
还是用老例子:n = 10 的数组,哈希函数 f(key) = key % 10,将 4,10,11,19,29,39 散列。
最后得到如下图:
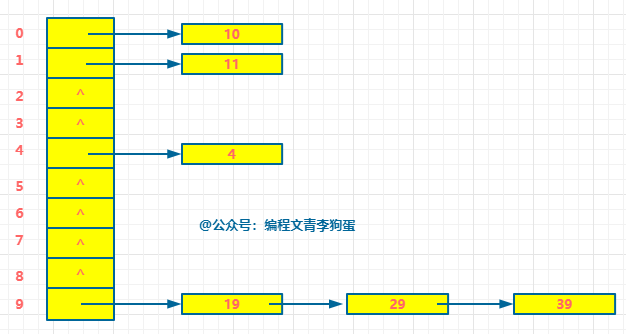
你看,链地址法就不会出现此坑被占,就得去找别的坑的情况。
大家一起蹲,这样就绝不会出现找不到地址的情况,而是直接插到对应的单链表中即可,所以插入的时间复杂度为 O(1)。
当然有得必有失,这样的情况必然造成了查找上的性能损耗,这里的查找的时间复杂度为 O(k),其中 k = n / 单链表条数。
好啦,到这里哈希表就讲完辣,是不是看起来还挺简单的。
哈希表作为非常高高高高高效的查找数据结构,丢掉了关键字之间反复无意义的比较,直接一步到位查找结果,非常顶。
这么看来它处理冲突啥的这点屁事就显得不是那么烦人了,毕竟有得有失才对嘛。
希望小婊贝们看完就能学会,如果有什么问题我们留言区见。
顺便大家不要忘记我的点赞在看呀,么么哒。
我是 Rocky0429,我们下次见~
推荐阅读 👍:ACM 选手带你玩转时间复杂度和空间复杂度
推荐阅读 👍:ACM 选手带你玩转数组
推荐阅读 👍:ACM 选手带你玩转链表
推荐阅读 👍:ACM 选手带你玩转栈和队列
推荐阅读 👍:ACM 选手带你玩转字符串
这篇关于ACM 选手带你玩转哈希表!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!