POI 2012 OKR - A Horrible Poem 题解

题目传送门

题目大意： 有一个长度为$n$的字符串，每次询问一个字串的最短循环节。

题解

最最暴力的做法：枚举长度 $len$，每次将该长度的字串与原串暴力匹配一遍。

然后考虑优化：

1.

显然 $len$ 一定是 $n$ 的因数，于是枚举 $len$ 的时候只需要枚举 $n$ 的因数即可。

2.

匹配可以用哈希来搞，但是如果将相邻的两节依次匹配的话还是很慢，最坏时间复杂度为 $O(n)$，于是如何进一步优化呢？

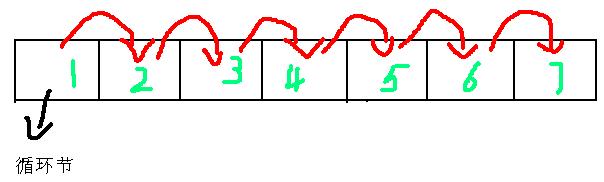
仔细观察一下匹配过程：

每一次匹配都是跟自己右边的匹配，然后我们又知道，hash的匹配无论多长都是 $O(1)$ 的，于是像这样子搞一搞——

将字符串复制一份，一个掐头，一个去尾，然后直接匹配，效果与两两匹配是一样的，因为现在上下对应的两个就是原来左右相邻的两个。

3.

part 1

经过尝试后，发现用 $O(\sqrt{n})$ 的方法来枚举因数还是不够优秀的（卡了半天常也过不去，可能是我太蒟了qaq），于是发掘一下更加优秀的做法。

一个数可以写成 $a_1^{b_1}{a}_2^{b_2}...$ 的形式，对于每个数，虽然因数可能很多，但是它的质因数个数实际少得可怜，并且每一个数的 $a$ 数组和 $b$ 数组都是可以预处理的，于是只需要枚举每一个质因数的指数就可以了。

但这种做法只是比 $O(\sqrt{n})$ 的做法快那么一点，所以总的时间复杂度依然不乐观……

综上，枚举因数似乎不大好做，于是需要换一种做法。

part 2

有一个看似很废的性质：假如长度 $x$ 是字符串的一个循环节，那么当 $x\ast k$ 也是总长的一个因数时，$x\ast k$ 也一定是一个循环节。

一开始觉得它很废是因为如果要得到 $x\ast k$ 首先肯定要得到 $x$，但那我都有 $x$ 了我还要 $x\ast k$ 有鸟用？

但是换一个角度看这条性质，它其实等价于——假如长度 $x$ 不是循环节，那么它的因数就都不是循环节。

于是根据这条性质，就得到了另一种做法，将 $len$ 的质因子都找出来，假如 $len/$某质因子 之后，得到的长度依然是一个循环节，那么 $len$ 就除以这个因子，否则就不除，因为除了之后得到的那个因数不是循环节，根据上述性质，我们并不能用这个奇怪的因数得到答案。

4.

卡常qwq

最后附上代码，还有些没讲到的细节里面有：

#pragma GCC optimize(3)
#include <cstdio>
#include <cstring>
#define ull unsigned long long
#define jinzhi 315ull
#define mod 2147463647ull
#define R register
#define maxn 500010int n,m;
char s[maxn];
inline int ch(char x){return x-'a';};
ull hash[maxn],power[maxn];
inline ull get(int l,int r){return (hash[r]-hash[l-1]*power[r-l+2]%mod+mod)%mod;};
//滚动哈希求子串的哈希值
inline bool check(const int x,const int y,int blo){return get(x,y-blo)==get(x+blo,y);}
//看长度blo是不是x~y这个子串的循环节
inline char nc()
{static char buf[1000010],*p1=buf,*p2=buf;return p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++;
}//读优
void read(int &x)
{x=0;char ch=nc();while(ch<'0'||ch>'9')ch=nc();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=nc();
}
bool v[maxn];
int prime[maxn],t=0;
void work()//线性筛素数
{for(int i=2;i<=maxn-10;i++){if(!v[i])prime[++t]=i;for(int j=1;j<=t;j++){if(prime[j]*i>maxn-10)break;v[prime[j]*i]=true;if(i%prime[j]==0)break;}}
}
int minfactor[maxn];
//每一个数的最小质因子，后面分解质因数时用到
void work2()//预处理minfactor
{for(int i=1;i<=t;i++){for(int j=1;j*prime[i]<=maxn-10;j++)if(!minfactor[prime[i]*j])minfactor[prime[i]*j]=prime[i];}
}
int a[maxn],st;int main()
{scanf("%d",&n);scanf("%s\n",s+1);work();work2();for(R int i=1;i<=n;++i)hash[i]=(hash[i-1]*jinzhi%mod+(ull)s[i])%mod;power[1]=1;for(R int i=2;i<=n;++i)power[i]=power[i-1]*jinzhi%mod;read(m);R int x,y;while(m--){read(x);read(y);int block(y-x+1);st=0;while(block!=1)a[++st]=minfactor[block],block/=minfactor[block];//用a存下将block分解质因数后的结果block=y-x+1;//记得还原blockfor(int i=1;i<=st;i++)if(check(x,y,block/a[i]))block/=a[i];printf("%d\n",block);}
}