hdu1556（线段树与BIT—区间更新）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1556Problem Description:

N个气球排成一排，从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了，你能帮他算出每个气球被涂过几次颜色吗？

Input

每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行，每行包括2个整数a b(1 <= a <= b <= N)。当N = 0，输入结束。

Output

每个测试实例输出一行，包括N个整数，第I个数代表第I个气球总共被涂色的次数。

Paste_Image.png

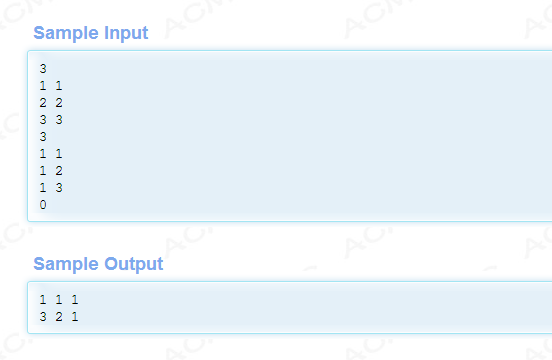
这是个区间更新问题，既可以用线段树做，也可以用树状数组。可以说能用树状数组做的题也可以用线段树做，反之不一定成立，但是BIT实现起来更方便，速度也更快。树状数组更新的时候在左端点+1，右端点的下一个-1，查询点也就变成求和了。

• 线段树：

#include <cstdio>
#include <cstring>
using namespace std;
const int MAX_N = 1 << 17;
int dat[2 * MAX_N - 1];//线段树
int arr[MAX_N];
int n;
void init(int t) {n = 1;while (n < t) n <<= 1;memset(dat, 0, sizeof(dat));memset(arr, 0, sizeof(arr));
}
void update(int a, int b, int k, int l, int r) {if (b < l || a > r) return ;闭区间[l, r]if (a <= l && r <= b) ++dat[k];else {update(a, b, k * 2, l, (l + r) >> 1);update(a, b, k * 2 + 1, ((l + r) >> 1) + 1, r);}
}
void add(int k, int l, int r) {for (int i = l; i <= r; ++i)arr[i] += dat[k];if (l == r) return ;//注意，否则死递归add(k * 2, l, (l + r) >> 1);add(k * 2 + 1, ((l + r) >> 1) + 1, r);
}
int main() {int t;while (scanf("%d", &t) != EOF && t) {init(t);for (int k = 0; k < t; ++k) {int a, b;scanf("%d%d", &a, &b);update(a, b, 1, 1, n);}add(1, 1, n);printf("%d", arr[1]);for (int i = 2; i <= t; ++i)printf(" %d", arr[i]);printf("\n");}return 0;
}

• 树状数组

#include <cstdio>
#include <cstring>
using namespace std;
const int MAX_N = 1e5 + 5;
int bit[MAX_N];
int n;
void add(int i, int x) {while (i <= n) {bit[i] += x;i += i & -i;}    
}
int sum(int i) {int s = 0;while (i > 0) {s += bit[i];i -= i & -i;}return s;
}
int main() {while (scanf("%d", &n) != EOF && n) {memset(bit, 0, sizeof(bit));for (int k = 0; k < n; ++k) {int a, b;scanf("%d%d", &a, &b);add(a, 1);add(b + 1, -1);}printf("%d", sum(1));for (int i = 2; i <= n; ++i)printf(" %d", sum(i));printf("\n");}return 0;
}