本文主要是介绍黑龙江省赛 A Path Plan(组合数学+Lindstrom-Gessel-Viennot Lemma定理)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
问题 C: A Path Plan
时间限制: 1 Sec 内存限制: 128 MB
提交: 55 解决: 26
[提交] [状态] [讨论版] [命题人:admin]
题目描述
WNJXYK hates Destinys so that he does not want to meet him at any time. Luckily, their classrooms and dormitories are at different places. The only chance for them to meet each other is on their way to classrooms from dormitories.
To simple this question, we can assume that the map of school is a normal rectangular 2D net. WNJXYK’s dormitory located at (0,y_1) and his classroom located at (x_1,0). Destinys’s dormitory located at (0,y_2) and his classroom is located at (x_2,0). On their way to classrooms, they can do two kinds of movement : (x,y)→(x,y-1) and (x,y)→(x+1,y).
WNJXYK does not want to meet Destinys so that he thinks that it is not safe to let his path to classroom from dormitory has any intersect point with Destinys ‘s. And then he wonders how many different paths for WNJXYK and Destinys arriving their classrooms from dormitories safely.
输入
The input starts with one line contains exactly one positive integer T which is the number of test cases.
Each test case contains one line with four positive integers x1,x2,y1,y2 which has been explained above.
输出
For each test case, output one line containing “y” where y is the number of different paths modulo 10^9+7.
样例输入
3 1 2 1 2 2 3 2 4 4 9 3 13
样例输出
3 60 16886100
提示
T≤1000
x1<x2,y1<y2
0 < x1,x2,y1,y2≤100000
For Test Case 1, there are following three different ways.
题意:两个人分别从(0,y1)-(x1,0)和(0,y2)-(x2,0),求他们路径不相交的方案数。
题解:比赛的时候用组合数学想了好久也没想到,最后没想到有这么个定理,还是太渣了,定理如下
对于一张无边权的DAG图，给定n个起点和对应的n个终点，这n条不相交路径的方案数为
det(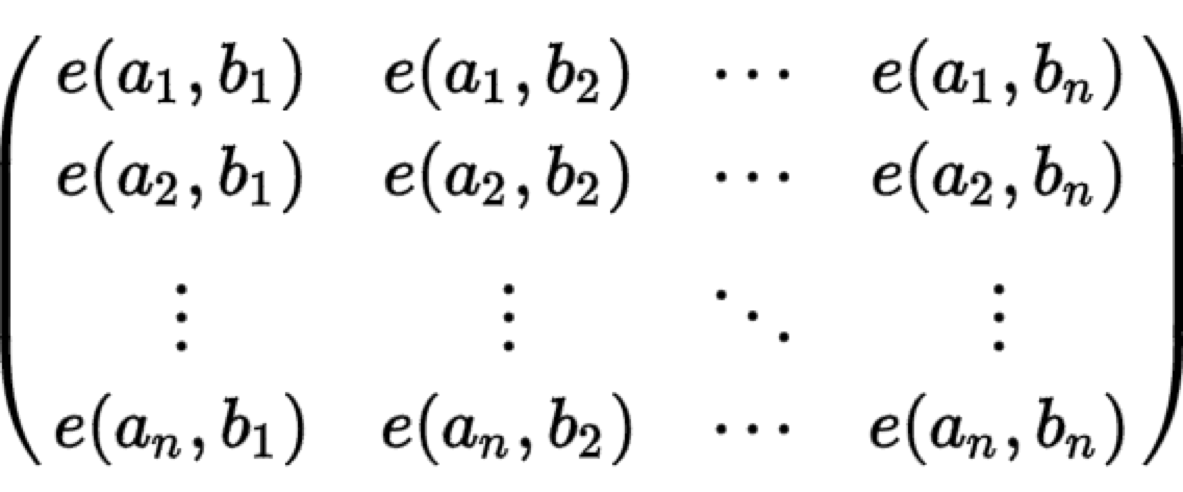
) （该矩阵的行列式）
其中e(a,b)为图点a到点b的方案数,如此答案只需要求解这个行列式即可。
2.行列式计算
https://blog.csdn.net/zhoufenqin/article/details/7779707
ps:求阶乘的逆元的小trick
inv[maxn] = qk_mod(fac[maxn],mod - 2);
for(int i = maxn - 1;i >= 0;i --) inv[i] = inv[i + 1] * (i + 1) % mod;
#include<bits/stdc++.h>
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define SI(i) scanf("%lld",&i)
#define PI(i) printf("%lld\n",i)
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const int MAX=1e6+7;
const int INF=0x3f3f3f3f;
const double eps=1e-8;
int dir[9][2]={0,1,0,-1,1,0,-1,0, -1,-1,-1,1,1,-1,1,1};
template<class T>bool gmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>bool gmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>void gmod(T &a,T b){a=((a+b)%mod+mod)%mod;}
typedef pair<ll,ll> PII;ll qpow(ll a,ll b)
{a%=mod;ll ans=1;while(b){if(b&1)ans=(ans*a)%mod;a=(a*a)%mod;b/=2;}return ans;
}ll fac[MAX];
ll C(ll a,ll b)
{return fac[a]*qpow(fac[a-b],mod-2)%mod*qpow(fac[b],mod-2)%mod;
}int main()
{fac[0]=1;for(int i=1;i<=200005;i++)fac[i]=fac[i-1]*i%mod;int T;scanf("%d",&T);while(T--){ll x1,x2,y1,y2;scanf("%lld%lld%lld%lld",&x1,&x2,&y1,&y2);ll ans=C(x1+y1,x1)*C(x2+y2,x2)%mod-C(x1+y2,x1)*C(x2+y1,x2)%mod;gmod(ans,(ll)mod);printf("%lld\n",ans);}
}
这篇关于黑龙江省赛 A Path Plan(组合数学+Lindstrom-Gessel-Viennot Lemma定理)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
