本文主要是介绍Python实现:在高斯计算中,如何操控客体分子穿过主体分子(或者客体分子围绕主体分子的任意方向旋转)和计算该过程能量变化(Gaussion09和Gaussion16输入文件为例,一键批量处理),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
注:该Python代码可以实现所有高斯(Gauss)计算输入文件的处理(特别是针对超分子体系的路径建模非常有用,也可以作为处理其它体系的参考)。具体来说,实现客体分子围绕主体分子的任意平面旋转任意角度或者实现客体分子从主体分子的任意平面的垂直方向穿过,并批量产生该路径上的高斯计算的输入文件。本实例以客体分子穿过主体分子为例。
。
正文如下:
超分子建模过程中,如果需要模拟客体分子穿过主体分子孔洞的过程(如小分子穿过大环分子)的能量变化,或者相互作用力的变化,具体实例如图一所示,球状富勒烯C60穿过一个分子环的过程。

图一
假设大环是由10个苯环通过σ键连接而成,形成[10]CPP,中文名称10环对苯撑,富勒烯C60分子作为客体分子,与大环会存在相互作用力,显而易见,在尺寸上这两者非常匹配,类似于在富勒烯球外面套上一根腰带,而这类分子是典型的超分子结构,理论计算对于研究这类体系尤为重要,特别是研究主体分子和客体分子间的相互作用力,扯远了,主客体相互作用不是本帖子讨论的重点。。。。。
回归正题,实现计算客体分子穿过主体分子这一过程的能量变化,设计这个模型的逻辑如下:
1. 总体思路是,富勒烯从一端到另一端的路径上设置多个点,可密可稀,对路径上的每一个点对应的超分子结构进行平面内的优化,求单点能做成二维图即可(也可以是刚性,默认中心的每一个点就是在该平面上的能量最低点,这样不用再优化结构,大大降低计算耗时)。
2. 这个路径是在[10]CPP大环的环平面对应垂直方向上,也就是说需要确定一个[10]CPP的环平面,可以默认为苯环之间的碳碳σ键均处在大平面上,也就是说,只要在这个位置找三个点就可以确定大环的化学平面(如C13-C4-C43三个碳原子对应的坐标点),再求三个坐标形成平面的法向量,再将得到的法向量转化为单位向量,以方便后续对坐标进行操作。
3. 在给定坐标基础上,只需要将富勒烯分子所有的坐标值在这个法向量上进行数学加减,即可代表在这个方向上的移动,移动的位置通过实际距离长度乘以单位法向量,即可得实际移动距离的具体坐标。
4. 通过距离批量命名输入文件名,得到对应高斯计算的输入文件。
5. 通过Gauss软件(主流是g09或者g16版本)计算得到每一个点能量,提取能量作图(非本文讨论内容)。
具体实现如下:
球形富勒烯C60穿过大环的过程的模拟,第一步是先得到优化后的超分子结构,如图二所示:

图二
用Gaussview打开该分子,存储为高斯输入文件(后缀为.gjf文件),这里需要注意,坐标顺序必须保持主体分子在前面,客体分子在后面,如图二中的数字编号,[10]CPP在前,C60在后。具体坐标如下所示:
%nprocshared=12
%mem=2500mb
%rwf=1,2000mb,2,2000mb,3,2000mb,4,2000mb,5,2000mb,6,2000mb,7,2000mb,8,2000mb,9,-1
%chk=xxxx.chk
# b3lyp/3-21g* c60-cycloparaphenylene0 1C 1.73732300 -6.65945200 0.02809900 C 1.02755200 -7.09867900 -1.09886500 C -0.35923100 -7.15166600 -1.09301500 C -1.09214200 -6.76784500 0.03963400 C -0.37754700 -6.49784200 1.21181700 C 1.01002500 -6.44545800 1.20553100 C -2.51785300 -6.37048700 -0.04431700 C -2.97016100 -5.74036500 -1.21000000 C -4.13845500 -4.99392400 -1.21062100 C -4.90312800 -4.84814500 -0.04645400 C -4.53591800 -5.60946900 1.07118000 C -3.36411000 -6.35602500 1.07264900 C -5.85139600 -3.71116200 0.03786900 C -5.90440600 -2.95677700 1.21537900 C -6.40004400 -1.65956700 1.21155600 C -6.85703100 -1.06756500 0.02933800 C -6.97558800 -1.88698300 -1.10270300 C -6.48354100 -3.18455800 -1.09801100 C -6.90248000 0.41140400 -0.06167900 C -6.40817300 1.02325000 -1.21997500 C -6.03985300 2.36013100 -1.21989300 C -6.14496300 3.13798100 -0.06066500 C -6.78453300 2.56780500 1.04839600 C -7.15754000 1.22949300 1.04716500 C -4.64005800 4.65248500 1.21041300 C -3.55537200 5.52027200 1.21350300 C -3.12994100 6.14885600 0.03711600 C -3.94425100 6.01574000 -1.09686700 C -5.02692900 5.14797700 -1.10110900 C -1.74018800 6.65969700 -0.04980100 C -1.00956300 6.44183900 -1.22441800 C 0.37809400 6.49263500 -1.22623300 C 1.08927100 6.76636900 -0.05284800 C 0.35328500 7.15304900 1.07679200 C -1.03349400 7.10088000 1.07840200 C 2.51547300 6.37190200 0.03499900 C 2.96709500 5.74379200 1.20198200 C 4.13620000 4.99840600 1.20469200 C 4.90210900 4.85217600 0.04139700 C 4.53622800 5.61330700 -1.07684800 C 3.36365400 6.35842800 -1.08049400 C -5.34104400 4.38075600 0.03042300 C 5.84993700 3.71487500 -0.04318300 C 5.90485500 2.96328900 -1.22243000 C 6.40060600 1.66622900 -1.22114400 C 6.85599400 1.07116200 -0.03981500 C 6.97232200 1.88772500 1.09456900 C 6.47981400 3.18517000 1.09247600 C 6.90179400 -0.40810500 0.04702900 C 6.41044100 -1.02363400 1.20472100 C 6.04105800 -2.36014200 1.20121100 C 6.14065700 -3.13376900 0.03855600 C 6.77748100 -2.56040100 -1.07033100 C 7.15289300 -1.22272400 -1.06519000 C 5.33527100 -4.37545100 -0.05446300 C 5.02398600 -5.14574800 1.07577100 C 3.94233000 -6.01463200 1.07152800 C 3.12606900 -6.14628300 -0.06125000 C 3.54840200 -5.51412100 -1.23685100 C 4.63187500 -4.64464500 -1.23359300 H 1.56541000 -7.34672800 -2.00967900 H -0.88545100 -7.43854900 -1.99928800 H -0.91060600 -6.18229600 2.10468700 H 1.52018700 -6.08573800 2.09444000 H -2.33707200 -5.72521100 -2.09203900 H -4.38431200 -4.40772900 -2.09088400 H -5.14544900 -5.57352400 1.96995500 H -3.07485500 -6.89299300 1.97196600 H -5.41551900 -3.32690100 2.11219600 H -6.28727900 -1.05339100 2.10620900 H -7.39935800 -1.48118400 -2.01720700 H -6.53116200 -3.77542700 -2.00849700 H -6.17975000 0.41790900 -2.09207500 H -5.53838000 2.76614300 -2.09331200 H -6.94304100 3.16412200 1.94303300 H -7.60200200 0.79948200 1.94069200 H -4.84870400 4.07052900 2.10418900 H -2.94650100 5.58820300 2.11037400 H -3.69015100 6.55329400 -2.00614400 H -5.60153600 5.01837500 -2.01422100 H -1.51756600 6.08167300 -2.11440800 H 0.91392000 6.17460700 -2.11655600 H 0.87701800 7.44229900 1.98377200 H -1.57408600 7.35169700 1.98681500 H 2.33260300 5.72835100 2.08305300 H 4.38139700 4.41318100 2.08579100 H 5.14722600 5.57782700 -1.97462900 H 3.07511300 6.89474600 -1.98042300 H 5.41762500 3.33561100 -2.11920300 H 6.28935500 1.06262500 -2.11768600 H 7.39476000 1.47994100 2.00878700 H 6.52580000 3.77355800 2.00465100 H 6.18445400 -0.42114700 2.07940700 H 5.54299500 -2.76899400 2.07524500 H 6.93213400 -3.15342900 -1.96782700 H 7.59563600 -0.79052700 -1.95849300 H 5.60050600 -5.01828500 1.98796400 H 3.69078200 -6.55483000 1.97993100 H 2.93823900 -5.58114600 -2.13297100 H 4.83796800 -4.06014100 -2.12631500 C 3.08629400 1.24678300 -1.18663000 C 2.65597700 2.32370100 -0.31319800 C 1.56703000 3.11047900 -0.66430900 C 0.85900600 2.85163200 -1.90693600 C 1.27520600 1.82434600 -2.74314300 C 2.41654400 1.00552200 -2.37623000 C -0.55709300 3.06239900 -1.67116800 C -1.49567400 2.24295600 -2.28288400 C -2.64937100 1.77240700 -1.53568200 C -2.81079900 2.14125400 -0.20797900 C -1.82534800 2.99500300 0.43065900 C -0.72662300 3.44561000 -0.28147900 C -3.26136200 1.16590200 0.76842500 C -2.55086700 1.41863900 2.01139700 C -2.13865100 0.35711200 2.80514200 C -2.41373400 -1.00859700 2.39275400 C -3.08356400 -1.24993700 1.20322000 C -3.52064900 -0.13964000 0.37401000 C -1.27238900 -1.82738300 2.75972000 C -0.85626900 -2.85461400 1.92351300 C 0.55986500 -3.06524800 1.68783300 C 1.49858600 -2.24587200 2.29955800 C 1.06222000 -1.17289700 3.17262700 C -0.29223400 -0.96870100 3.39765200 C 2.92698600 -0.41057000 1.96370400 C 3.35478400 0.52527600 1.03081100 C 3.52319500 0.13647400 -0.35745300 C 3.26430100 -1.16913700 -0.75185200 C 2.81349900 -2.14436900 0.22468200 C 2.65226100 -1.77547900 1.55242000 C 2.14154100 -0.36018800 -2.78858800 C 2.55380600 -1.42178700 -1.99480700 C 1.82818700 -2.99805800 -0.41386800 C 0.72937800 -3.44822400 0.29824800 C -1.56436700 -3.11370700 0.68080900 C -2.65326800 -2.32684700 0.32968100 C -3.35198300 -0.52834000 -1.01420900 C -2.92402900 0.40755000 -1.94701700 C -1.05929900 1.16995800 -3.15594000 C 0.29511600 0.96568500 -3.38110800 C 1.94365300 -0.03842200 2.96525300 C -0.82734600 0.38054400 3.42607800 C -1.66690800 2.55081600 1.80312300 C 0.58416400 3.47687300 0.34014400 C 2.81871800 1.87494100 1.05829200 C 0.83027500 -0.38358800 -3.40955200 C -1.94069100 0.03545200 -2.94851500 C -2.81592100 -1.87796100 -1.04170800 C -0.58141700 -3.47979100 -0.32355700 C 1.66973200 -2.55380600 -1.78644100 C -1.87700800 -2.23334000 -2.00088800 C -1.42953700 -1.25416300 -2.97509800 C -0.73573500 -3.05340800 -1.63463700 C 0.41602800 -2.57836600 -2.38169300 C -0.01295600 -1.46817700 -3.21040300 C -0.41306600 2.57533700 2.39827700 C 0.73858100 3.05044500 1.65128300 C 1.87994000 2.23039500 2.01752600 C 1.43248600 1.25119500 2.99177500 C 0.01591200 1.46514200 3.22701500
最终python代码如下,复制粘贴进pycharm即可,使用前需要安装numpy、linecache库,安装方法请自行google或者baidu,简单到令人发指,time库和decimal库python已自带,直接调用即可。
注意:高斯输入文件需要放入代码所在的同一文件夹下,否则不能执行:
"""
通过三个化学点求法向量和单位法向量,并实现客体分子绕着主体分子平面旋转任意角度或者现客体分子从主体分子平面的垂直方向穿过,并批量产生该路径上的高斯计算的输入文件
"""import numpy
import linecache
from decimal import Decimal# 将向量转化为单位向量,如果向量是0向量,返回原向量
def UnitVect(v):norm = numpy.linalg.norm(v) # 求范数if norm == 0:return vreturn v / norm# 传入三个坐标,求三点确定的面对应的法向量
def NormVect(coord_1, coord_2, coord_3):a = numpy.array(coord_1)b = numpy.array(coord_2)c = numpy.array(coord_3)global hh = numpy.cross(a - b, a - c)print(f"法向量是:{h}")x = UnitVect(h)return x# 小数的区间变化函数定义
def frange(x, y, jump):while Decimal(str(x)) < Decimal(str(y)):yield xx += float(Decimal(str(jump)))def first_coord_line():# 将输入的数字全部加 n,n指的是当第m行识别到有 # 字符之后的第5行为第一个计数的坐标,即:n = m + 4,当遇到有 # 字符时中断for循环# range中的10可以改变,一般 # 出现在前10行以内,为了减小计算量限制在10以内(如果文件很大,又没有 # 出现会造成计算资源浪费)for m in range(1, 10):mark_line = linecache.getline(f'{filename}', m)mark_x = mark_line[0]if mark_x == '#':n = m + 4breakreturn ndef generate_NormVect_by_AtomNum():# 这里获取第一个坐标coord1_line = linecache.getline(f'{filename}', atom_1 + n)coord1_line = coord1_line.split()coord_name1, *coord_temp = coord1_linecoord_1 = [float(x) for x in coord_temp]print(f"第一个原子是:{coord_name1}, 坐标是:", coord_1)# 这里获取第二个坐标coord2_line = linecache.getline(f'{filename}', atom_2 + n)coord2_line = coord2_line.split()coord_name2, *coord_temp = coord2_linecoord_2 = [float(x) for x in coord_temp]print(f"第二个原子是:{coord_name2}, 坐标是:", coord_2)# 这里获取第三个坐标coord3_line = linecache.getline(f'{filename}', atom_3 + n)coord3_line = coord3_line.split()coord_name3, *coord_temp = coord3_linecoord_3 = [float(x) for x in coord_temp]print(f"第三个原子是:{coord_name3}, 坐标是:", coord_3)# 接下来对坐标进行操作NormVect_val = NormVect(coord_1, coord_2, coord_3)print(f"单位法向量是:{NormVect_val}")# 写入一个文件,用于放最后结果with open("result.txt", mode="w", encoding="utf-8") as f:f.write(f"第一个原子是:{coord_name1}, 坐标是:{coord_1}\n")f.write(f"第二个原子是:{coord_name2}, 坐标是:{coord_2}\n")f.write(f"第三个原子是:{coord_name3}, 坐标是:{coord_3}\n")f.write(f"法向量是:{h}\n")f.write(f"单位法向量是:{NormVect_val}")return NormVect_valdef rotat_results():initial_pos = float(input("请输入旋转分子起始角度(e.g. -90):"))final_pos = float(input("请输入旋转分子终点角度(e.g. 90):"))CalGrid = float(input("请输入计算格点密度(e.g. 5表示每5°取一个点):"))for i_distance in frange(initial_pos, final_pos, CalGrid):i_distance_decimal = Decimal(i_distance).quantize(Decimal('0.00'))# 读取文件每一行数据with open(f"{i_distance_decimal}_rotate.gjf", mode="w", encoding="utf-8") as f:for x in range(1, n + 1):data_line = linecache.getline(f'{filename}', x)f.write(f"{data_line}")for y in range(n + 1, n + atoms_num_plane + 1):data_line = linecache.getline(f'{filename}', y)f.write(f"{data_line}")for z in range(n + atoms_num_plane + 1, n + atoms_num_all + 1):coord_line = linecache.getline(f'{filename}', z)coord_line = coord_line.split()coord_name, *coord_temp = coord_linecoord = [float(p) for p in coord_temp]a = numpy.array(coord)b = numpy.array(NormVect_val)x = float(str(i_distance_decimal))# 将度数转换为弧度angle_degrees = xangle_radians = numpy.radians(angle_degrees)# 计算旋转矩阵cos_theta = numpy.cos(angle_radians)sin_theta = numpy.sin(angle_radians)rotation_matrix = numpy.array([[cos_theta + (1 - cos_theta) * b[0] ** 2,(1 - cos_theta) * b[0] * b[1] - sin_theta * b[2],(1 - cos_theta) * b[0] * b[2] + sin_theta * b[1]],[(1 - cos_theta) * b[1] * b[0] + sin_theta * b[2],cos_theta + (1 - cos_theta) * b[1] ** 2,(1 - cos_theta) * b[1] * b[2] - sin_theta * b[0]],[(1 - cos_theta) * b[2] * b[0] - sin_theta * b[1],(1 - cos_theta) * b[2] * b[1] + sin_theta * b[0],cos_theta + (1 - cos_theta) * b[2] ** 2]])# 进行旋转操作,并写入文件rotated_vector = numpy.dot(rotation_matrix, a)d = [str(i) for i in rotated_vector]e = ' '.join(d)f.write(f"{coord_name} {e}\n")f.write("\nPd 0\nlanl2dz\n****\nO C N H F 0\n6-31g*\n****\n\nPd 0\nlanl2dz\n")f.write("\n")def cross_results():initial_pos = float(input("请输入起始位置(e.g. -5,表示距离平面-5.0 Å):"))final_pos = float(input("请输入终点位置(e.g. 5,表示距离平面5.0 Å):"))CalGrid = float(input("请输入计算格点密度(e.g. 0.5表示每0.5 Å取一个点):"))for i_distance in frange(initial_pos, final_pos, CalGrid):i_distance_decimal = Decimal(i_distance).quantize(Decimal('0.00'))# 读取文件每一行数据with open(f"{i_distance_decimal}_cross.gjf", mode="w", encoding="utf-8") as f:for x in range(1, n + 1):data_line = linecache.getline(f'{filename}', x)f.write(f"{data_line}")for y in range(n + 1, n + atoms_num_plane + 1):data_line = linecache.getline(f'{filename}', y)f.write(f"{data_line}")for z in range(n + atoms_num_plane + 1, n + atoms_num_all + 1):coord_line = linecache.getline(f'{filename}', z)coord_line = coord_line.split()coord_name, *coord_temp = coord_linecoord = [float(p) for p in coord_temp]a = numpy.array(coord)b = numpy.array(NormVect_val)x = float(str(i_distance_decimal))cross_vector = a + b * xd = [str(i) for i in cross_vector]e = ' '.join(d)f.write(f"{coord_name} {e}\n")f.write("\n")if __name__ == "__main__":filename = input("请输入文件名:")atoms_num_all = int(input("请输入原子数:"))atoms_num_plane = int(input("请输入主体分子原子数:"))atom_1, atom_2, atom_3 = eval(input("三个原子确定的化学平面(请输入三个原子序号 e.g. 1,2,3):"))n = first_coord_line()NormVect_val = generate_NormVect_by_AtomNum()user_input = input("请输入一个数字(1 或 2),1代表旋转分子操作,2代表平移分子操作: ")if user_input == "1":rotat_results()if user_input == "2":cross_results()else:print("输入无效,请输入1或2")上面代码运行后,按照下面提示,输入相应内容即可:
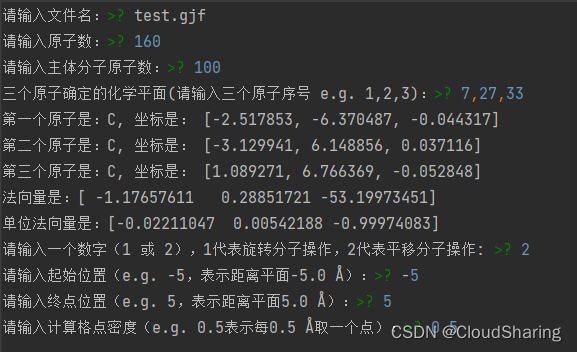
至此输入文件制作完成,将得到的高斯输入文件传入高斯软件进行计算,最后统计得到的能量,origin做二维图即可展现该路径上的能量变化。
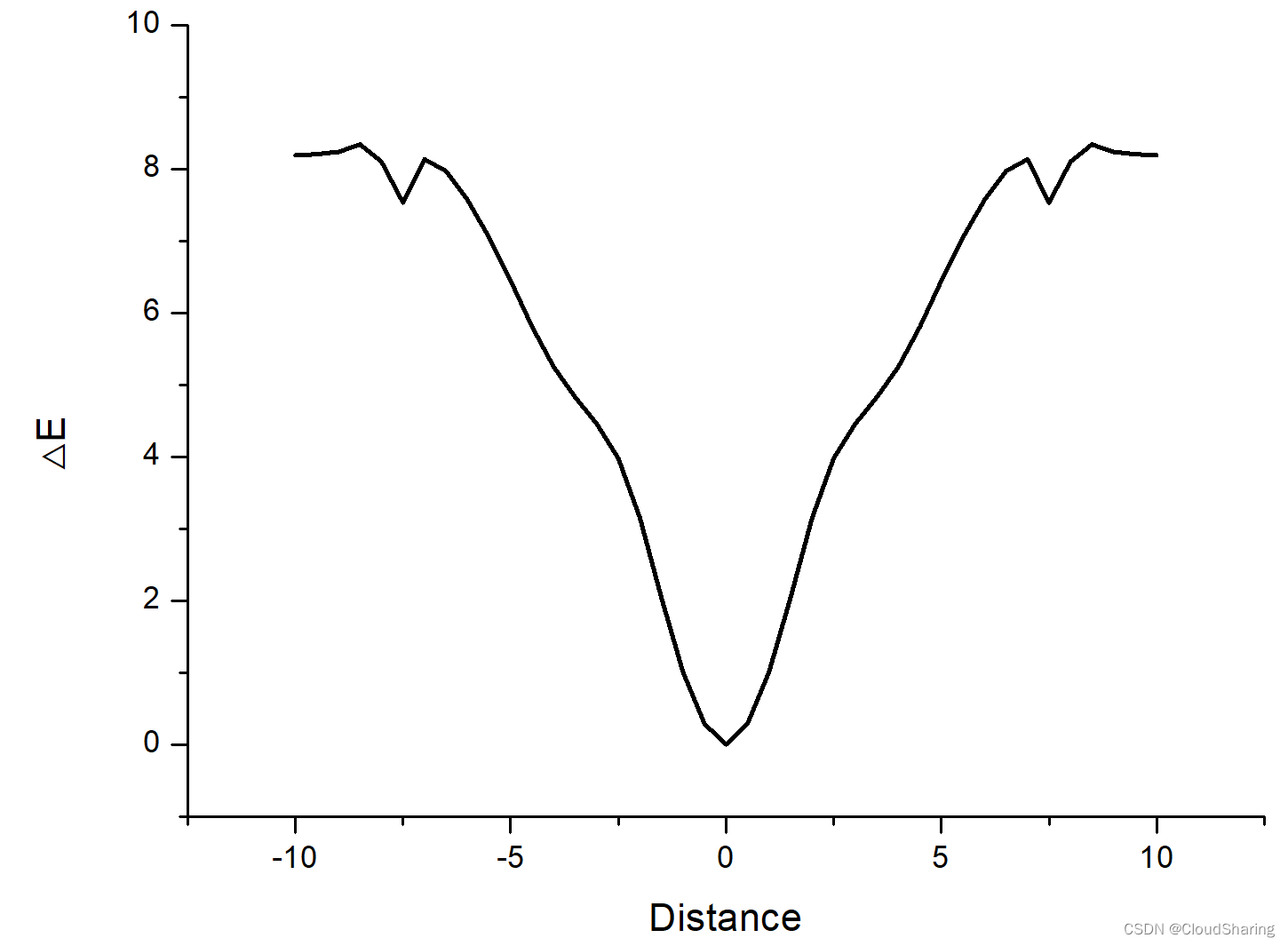
如下图所示,得到能量变化图(显然很符合化学常识,在尺寸匹配情况下,富勒烯分子在大环内能量最低,也意味着富勒烯分子在环内比较稳定,且从数据可以看出富勒烯分子要逃离大环束缚需要至少 8.3 kcal 以上的能量。):
这篇关于Python实现:在高斯计算中,如何操控客体分子穿过主体分子(或者客体分子围绕主体分子的任意方向旋转)和计算该过程能量变化(Gaussion09和Gaussion16输入文件为例,一键批量处理)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




