数据结构代码题------树相关day01 序幕

本文主要是介绍数据结构代码题------树相关day01 序幕，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

数据结构代码题----树

题目01

已知一颗二叉树，按照顺序存储结构进行存储，设计一个算法，求编号分别i和j的两个节点的最近的公共祖先结点的值。

算法分析

1、首先是对二叉树的顺序结构进行介绍
在这里插入图片描述
结合以上的图片描述，对于二叉树中，顺序存储的设计性质如下：

祖先结点的下标为i/2或者j/2
已知一个祖先结点，其儿子结点的下标为i*2

2、寻找最近公共祖先结点

思路：
想象下，现在二叉树的深度非常的大，若i和j分别在不同的子树系统中，若要找到最近的公共祖先结点，要怎么做呢？？？

答案

答案每次进行i和j进行比较，选择较大者进行比较并取i/2或者j/2进行设计，进行递归，直到最后的i=j便是最近的最佳的公共直接点。

其实现代码如下：

typedef ElemType int; 
ElemType Search_Common_Ancester(int A[], int i,int j){if(A[i] != NULL && A[j] != NULL){//设置起始条件while(i != j){if(i > j){i = i/2;//进行寻找祖先}else{j = j/2;//进行交换}}//这里退出了循环，因此有i=jreturn A[i];//返回结果
}}

核心代码：

//设置起始条件while(i != j){if(i > j){i = i/2;//进行寻找祖先}else{j = j/2;//进行交换}}//这里退出了循环，因此有i=jreturn A[i];//返回结果

递归实现：

typedef ElemType int; 
ElemType Search_Common_Ancester(int A[], int i,int j){if(A[i] == NULL  || A[j] == NULL){return 0;}if(i == j){return A[i];//递归出口}if(i < j){//j的位置大，因此需要对其进行向上寻找Search_Common_Ancester(A,i,j/2);}else{Search_Common_Ancester(A,i/2,j);}
}

题目02

二叉树中序遍历-----非递归实现

分析
结合下面的例子图进行讲解：

在这里插入图片描述
中序遍历非递归的设计口诀：

入栈向左一直走，出栈访问右子树

算法思路：

初始化一个数据结构栈
对于从根节点开始，依次入栈左子树的左节点，直到结点为NULL，
同时对其进行栈顶元素的出栈
出栈之前要先判断右子树是否存在
右子树存在则入栈
不存在则出栈并访问。

其实现的流程图大致如下：

在这里插入图片描述
结合以上的分析对其进行给出核心代码如下：

while(p != NULL ｜｜ !isEmpty(S)){if(p != NULL){//入栈向左一直走push(S,p);p = p->lchild;}else{//当到达空结点pop(S,p);visit(p->data);//标记访问结点p = p->rchild;//出栈访问右子树}

完整代码：

typedef struct TNode{ElemType data;struct TNode* lchild, *rchild;
}TNODE;
//中序遍历
void MiddleTraverse(Tree root){InitStack(S);root =  p;
//起始条件while(p != NULL ｜｜ !isEmpty(S)){if(p != NULL){//入栈向左一直走push(S,p);p = p->lchild;}else{//当到达空结点pop(S,p);visit(p->data);p = p->rchild;}}
}

题目03
二叉树后序遍历----非递归！！！

分析

二叉树的后序遍历是三种遍历序列中非递归实现最为困难的一个，需要对出栈元素进行多次判断，这里以上面的二叉树的进行分析：
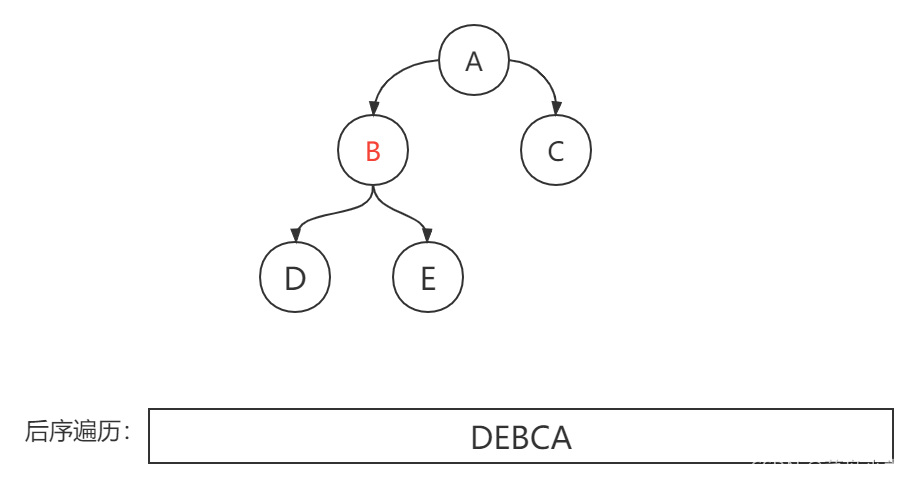
在这里插入图片描述
后序遍历的实现依旧是需要借助于数据结构栈进行操作，因此我们试着先将其左子树入栈，向左一直走如下图：

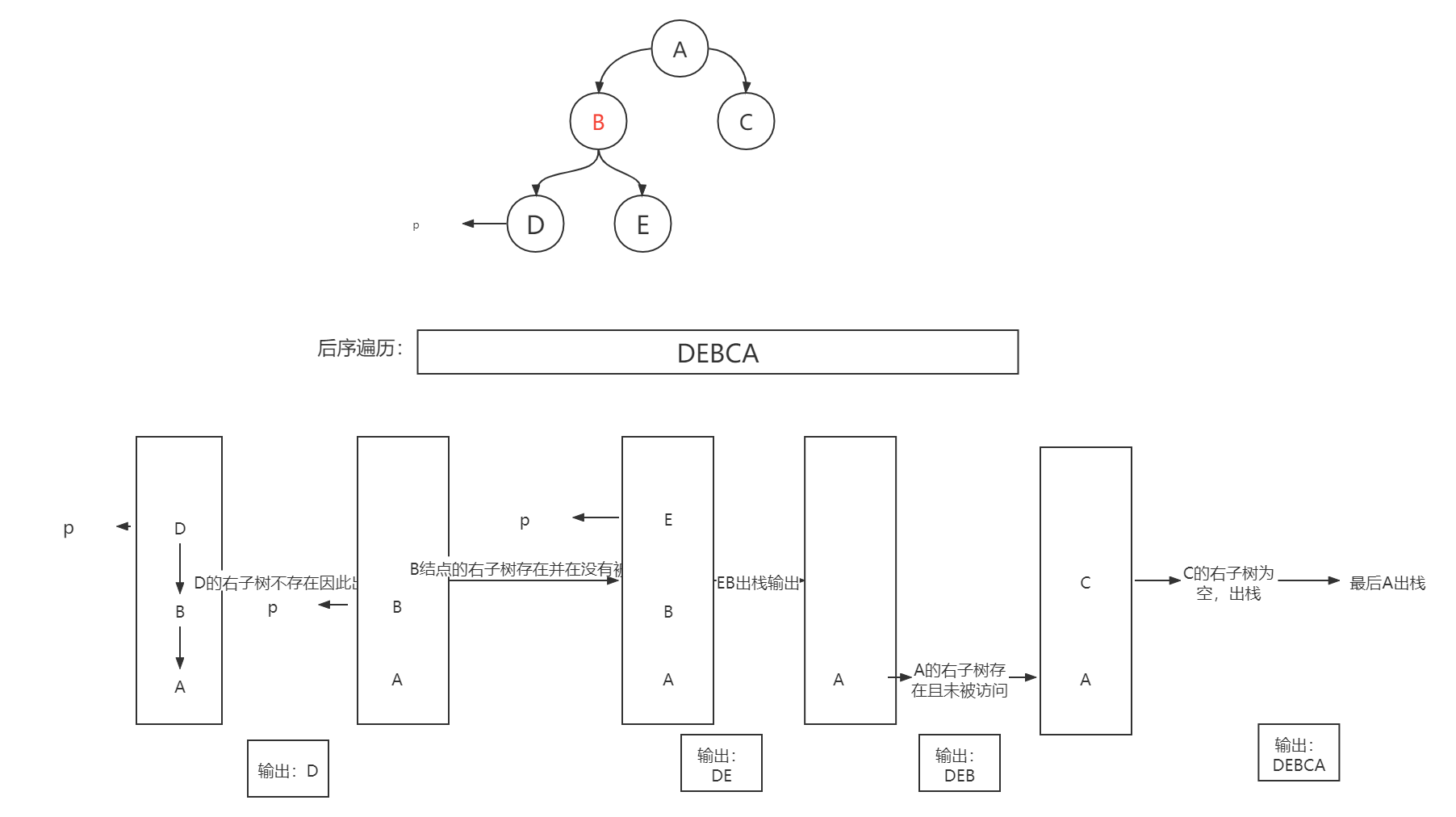
大致实现的思路便是：

入栈左子树直到左子树为NULL
获取到栈顶的结点p-----采用GetTop(S,p)
对栈顶的结点进行右子树是否访问以及是否为NULL的检测，
！！！！！！！！！！记住！！！
这里是对栈顶结点的右子树的是否为空和是否之前被访问过进行判断。
若不为空也没有被访问到，则该元素进栈，指向其左子树进行判断
若为空或者已经被访问到了，则栈顶元素直接出栈，并设置标记已经访问过
循环这个过程。

助记口诀：入栈向左一直走，判定(右子树)，出栈访问，标记，重置初始指针

下面是核心实现代码：

	//核心代码if(p!=NULL){//入栈向左一直走push(S,p);//入栈p = p->lchild;}else{//这时p为空，说明左子树走到尽头了GetTop(S,p);//获取栈顶元素//对栈顶元素进行检测if(p->rchild != NULL && p->rchild != r){//不为空，没有被访问p = p->rchild;//转到右子树push(S,p);//入栈p = p->lchild;//左子树继续}else{//若已经被访问pop(S,p);//出栈visit(p->data);//访问r = p;//标记已经访问p=NULL;//重置为NULL方便下一次使用}

完整代码：


typedef struct TNode{ElemType data;struct TNode* lchild, *rchild;
}TNODE,*BiTree;
//非递归方法实现后序遍历
void OrderTaverse(BiTree root){if(root == NULL){return ;}InitStack(S);//初始化一个栈TNode * p = root;//操作指针TNode * r = NULL;//标记访问指针while(! isEmpty(S)){//核心代码if(p!=NULL){//入栈向左一直走push(S,p);//入栈p = p->lchild;}else{//这时p为空，说明左子树走到尽头了GetTop(S,p);//获取栈顶元素//对栈顶元素进行检测if(p->rchild != NULL && p->rchild != r){//不为空，没有被访问p = p->rchild;//转到右子树push(S,p);//入栈p = p->lchild;//左子树继续}else{//若已经被访问pop(S,p);//出栈visit(p->data);//访问r = p;//标记已经访问p=NULL;//重置为NULL方便下一次使用}}}
}

题目04

二叉树层次遍历非递归实现

其遍历实现图如下：
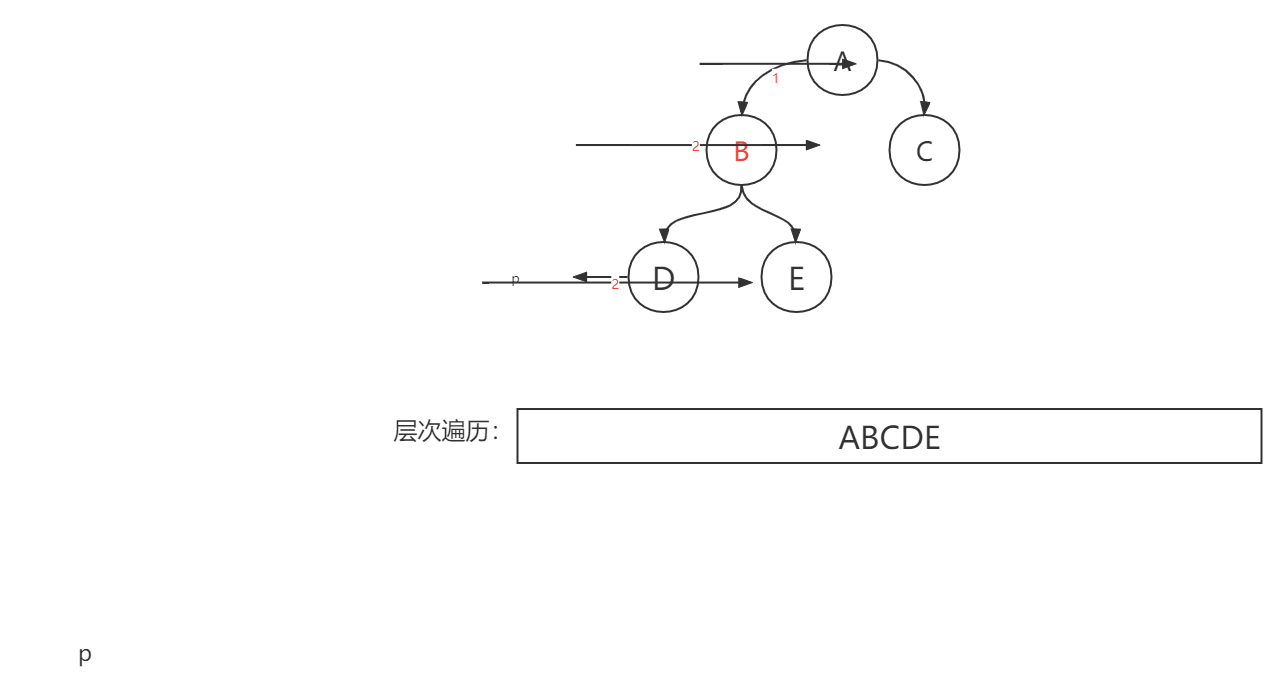
在这里插入图片描述
结合其二叉树的递归实现顺序，我们发现，这个实现的遍历结果采用队列的方式，对于其先进先出的特性非常符合，因此层次遍历采用队列实现

其实现过程图如下：
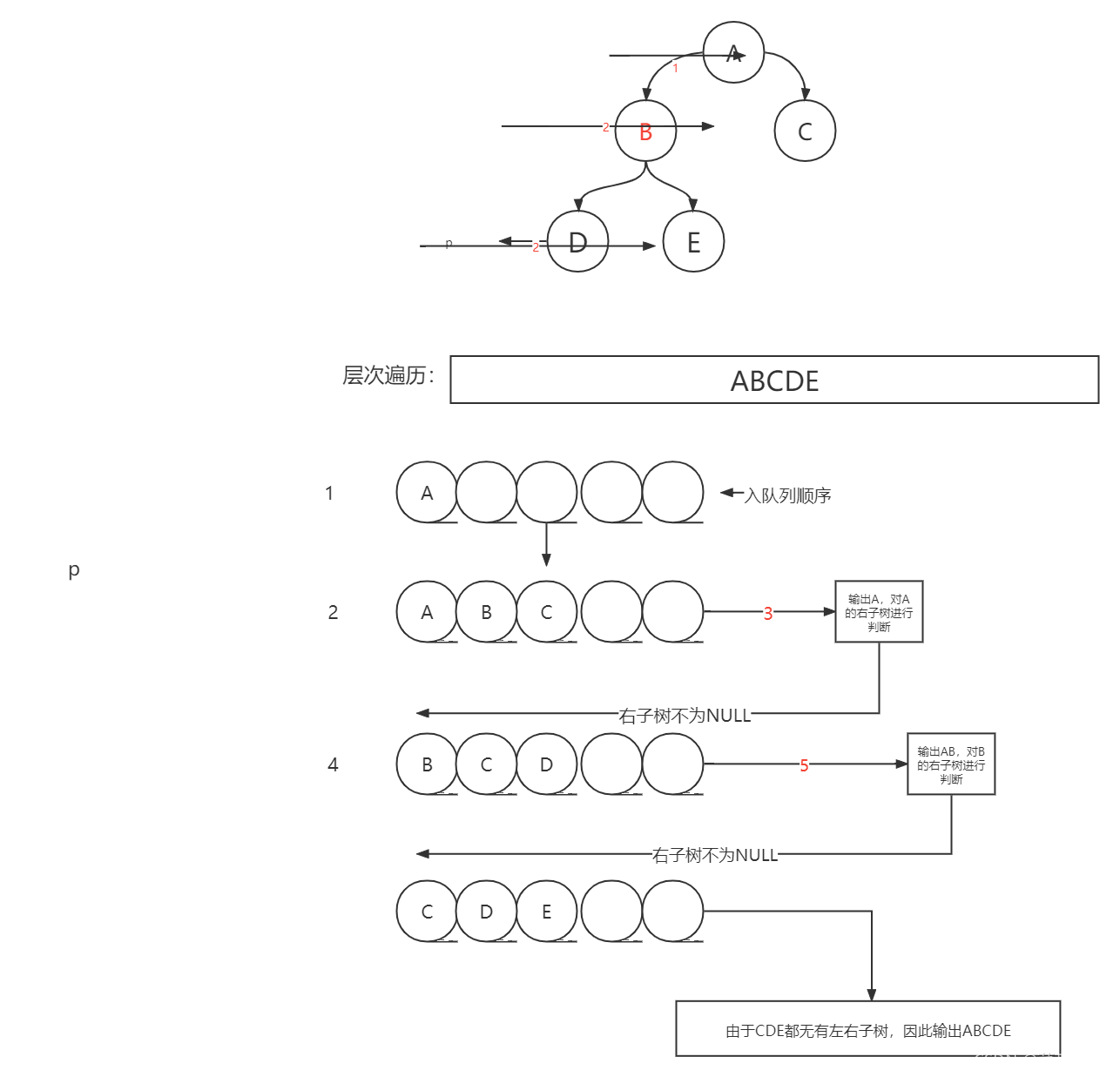
在这里插入图片描述
实现思路：

根节点判断是否为NULL
根节点入队，
出队访问左右子树
若左子树不为空，则访问左子树
若右子树不为空，访问右子树
队列为空，则循环停止

实现核心代码如下：

	while(!isEmpty(Q)){DeQueue(Q,p);//出队列visit(p->data);//访问数据//有左子树入队列if(p->lchild != NULL){EnterQueue(Q,p->lchild);}//右子树入队列if(p->rchild != NULL){EnterQueue(Q,p->rchild);}}

完整代码：

typedef struct TNode{ElemType data;struct TNode* lchild, *rchild;
}TNODE,*BiTree;
//层次遍历代码
void BehindTraverse(BiTree root){if(root == NULL){return ;}InitQueue(Q);//初始化队列TNODE *p;//根节点如队列EnterQueue(Q,root);while(!isEmpty(Q)){DeQueue(Q,p);//出队列visit(p->data);//访问数据//有左子树入队列if(p->lchild != NULL){EnterQueue(Q,p->lchild);}//右子树入队列if(p->rchild != NULL){EnterQueue(Q,p->rchild);}}
}