本文主要是介绍极值图论基础,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,普通子图禁图
二,Turan问题
三,Turan定理、Turan图
1,Turan定理
2,Turan图
四,以完全二部图为禁图的Turan问题
1,最大边数的上界
2,最大边数的下界
五,以偶圈为禁图的Turan问题
六,Ramsey问题
1,Ramsey定理
2,Ramsey问题
一,普通子图禁图
参考普通子图
普通子图禁图指的是,给出一些具体的图,描述某个图不以这些具体的图作为普通子图。
二,Turan问题
给出一个图集F,求以F为普通子图禁图的图的最大边数,以及取到最大值的图是什么?
即,一个图最多能有多少条边,使得不以F中的任意图为普通子图。
PS:我们只关心简单图,否则如果2个点之间连无穷条多重边,那就没意义了。
PS:取到最大值的图称为极图,如果有唯一的极图,我们就说满足条件的极图是什么,不需要赘述边数了。
三,Turan定理、Turan图
1,Turan定理
以完全图K(r+1)为禁图的极图是平衡完全r部图,且没有其他极图。
2,Turan图
n个点的平衡完全r部图也叫图兰图Tr,n,即把n个点平均分成r份得到的完全r部图。
所以也可以说以完全图K(r+1)为禁图的n个点的图,唯一的极图是图兰图Tr,n。
比如,以完全图K4为禁图的8个点的图,唯一的极图是T3,8:
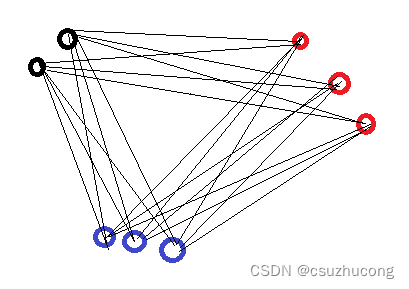
实际上,图兰图Tr,n的边数就是,其中p=n/r
比如T3,8,n=8,r=3,p=2,
四,以完全二部图为禁图的Turan问题
1,最大边数的上界
定理:对于任意s>=t>=2,存在常数C,对于任意n,以完全二部图Ks,t为禁图的图的边数不超过
猜想:对于任意s>=t>=2,以完全二部图Ks,t为禁图的图的最大边数为
其中,θ是渐进相等的符号。
2,最大边数的下界
存在常数C,对于任意t>=2,任意s>C^t,以完全二部图Ks,t为禁图的图的最大边数为
已经很接近上面的猜想了,但还没完全解决。
五,以偶圈为禁图的Turan问题
定理:对于任意k>=2,以2k个点构成的偶圈为禁图的图的边数不超过
猜想:对于任意k>=2,以2k个点构成的偶圈为禁图的图的边数为
六,Ramsey问题
1,Ramsey定理
对于任意的s>1,t>1,一定存在一个整数N,对于任意N个点的图,要么存在s个点两两相连,要么存在t个点两两不相连。
我们把满足条件的最小N记做R(s,t)
2,Ramsey问题
Ramsey问题就是R(s,t)的大小和性质。
这篇关于极值图论基础的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







