使用python绘制无边框ECG信号-可用于论文插图-小白版

本文主要是介绍使用python绘制无边框ECG信号-可用于论文插图-小白版，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

用python绘制一个心电信号

最近在写大论文，由于自己做的是心电信号难免要做一些心电信号的插图，然后在写论文的时候有的时候要用真实信号有的时候需要用到示意图，这里面的其他部分使用Visio绘制的，但是前面的心电信号部分，如果是写论文截图肯定不是一个好的选择，他一定比插入图片的清晰度要低，如果导入到origin中又有点麻烦,所以我就使用python的心电信号的库结合matplot中的plt中关闭坐标轴显示的方式来打印出一段真实的心电信号，然后后续可以作为插入到论文中的一个素材。

在这里插入图片描述

1.安装pywt库用于生成模拟心电信号

绘制真实的心电信号插图，可能有人想到的就是是不是需要加载一个数据集中的心电信号，然后数据集中的心电信号也不一定是干净的，因此大部分人看别人可能直接画一个示意图就结束了，但是pywt库中，有一段可以直接加载的ecg信号，因此我们可以考虑使用数据库中自带的信号来绘制心电图，或者说也可以后期加载自己的数据库。

直接使用pip命令安装即可

pip install pywt

之后使用pywt中的pywt.data.ecg()来生成一个模拟的心电信号，请添加图片描述
实现的代码如下

import matplotlib.pyplot as plt
import pywtecg = pywt.data.ecg() # 生成心电信号plt.plot(ecg)
plt.show()

2.调整心电信号颜色去掉边框

最终输出的结果是这样的，最后我们只要保存下来就可得到一个无边框的心电信号图像了
在这里插入图片描述
代码如下

import matplotlib.pyplot as plt
import pywtecg = pywt.data.ecg() # 生成心电信号plt.plot(ecg)
plt.plot(ecg,color='black')
# 关闭坐标轴
plt.axis('off')
plt.show()

3.保存图片

保存图片有两种方式一种是直接手动保存，直接点击下面的保存图片即可。
在这里插入图片描述
第二种是在代码里保存，使用plt.savefig(路径+文件名+.jpg/png)保存，如果plt.savefig()中只写文件名字那就是保存在相对路径下，需要将plt.show()替换为plt.savefig('ecg.jpg')
plt.savefig()和plt.show()不能同时使用，如果同时使用只会有效一个，例如你先使用plt.show()显示了图片，之后你在想使用plt.show()保存你会发现保存了一张空白图像，这是新手宝宝需要注意的地方

import matplotlib.pyplot as plt
import pywtecg = pywt.data.ecg() # 生成心电信号plt.plot(ecg)
plt.plot(ecg,color='black')
plt.axis('off')
# plt.show()
plt.savefig('ecg.jpg')

保存之后就在目标路径下得到了一张无边框的清晰的心电信号图片
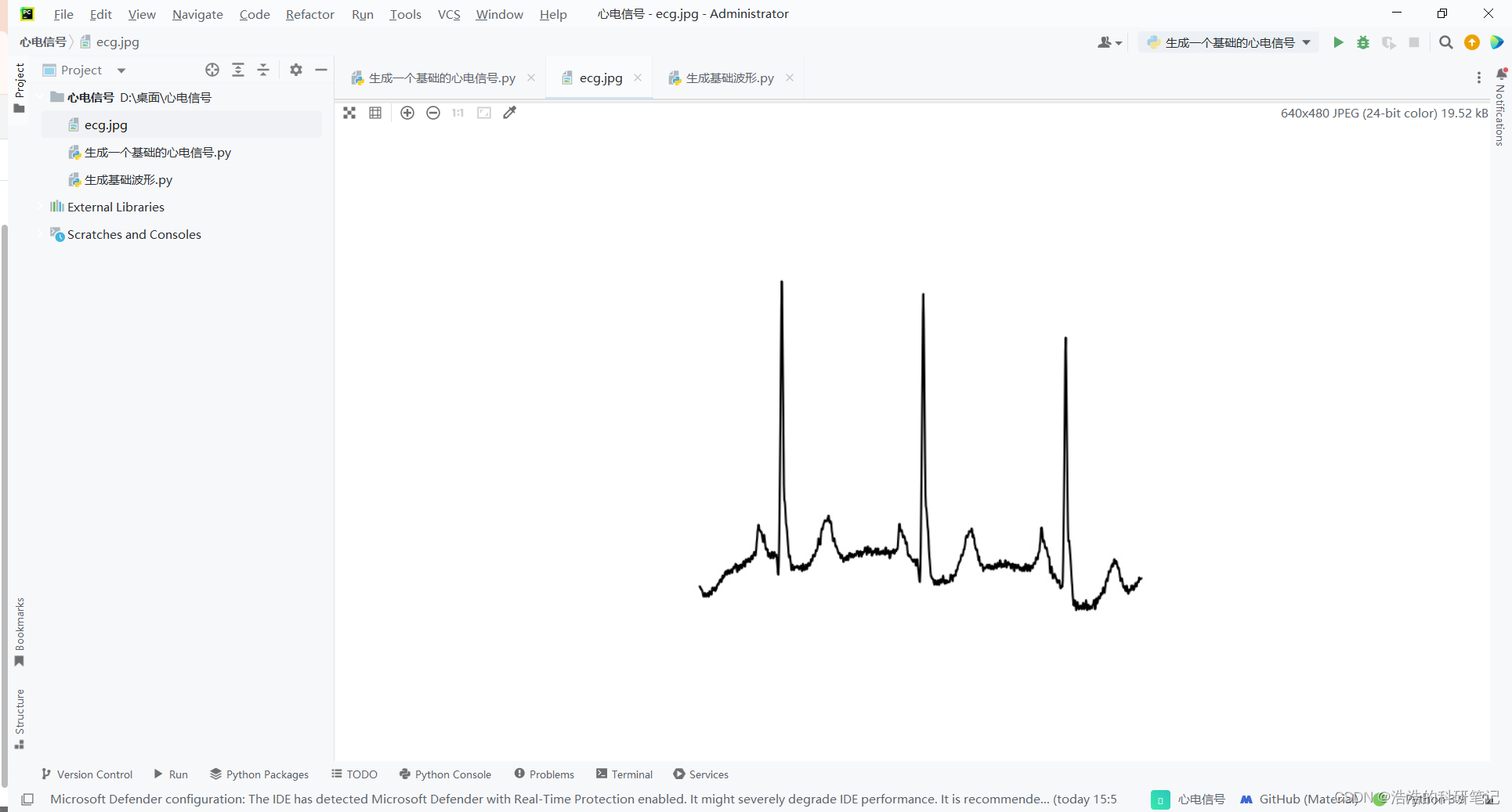
在这里插入图片描述

4.绘制去噪之后的心电信号

心电信号去噪的方式又很多种，包括中值滤波，巴特沃斯，等等，如果你对去噪感兴趣请拜读愚作
心电信号去噪python
在这里我们使用巴特沃斯带通滤波器来获得去噪之后的信号
在这里插入图片描述
代码如下：

import matplotlib.pyplot as plt
import pywt
from scipy import signalecg = pywt.data.ecg() # 生成心电信号def singnal_fliter(data, frequency=256, highpass=20, lowpass=1):[b, a] = signal.butter(3, [lowpass / frequency * 2, highpass / frequency * 2], 'bandpass')Signal_pro = signal.filtfilt(b, a, data)return Signal_proecg = pywt.data.ecg() # 生成心电信号
fliter_ecg = singnal_fliter(ecg)#滤波plt.plot(fliter_ecg,color='black')
plt.axis('off')
# plt.show()
plt.savefig('ecg.jpg')