空谈数字化营销，你还没有升级迭代独立网站吗？

互联网经济大势下，创业公司如雨后春笋般涌现，导致了更加激烈的市场竞争。而这些企业想要脱颖而出自然就变得更难了，这也使得企业开始追求打破局面的方式。

企业之间的竞争已经不单单局限在产品方面的竞比，营销方式同样成为了重要影响因素。在几乎处处都要讲究数字化的互联网经济下，企业要发展壮大，必然要进行数字化营销。

对于中小企业而言，没有强大的营销团队，充足的资金，专业的知识，在营销过程中就容易碰壁，而此时LTD营销SaaS系统则为中小企业提供了一条解决之道。

先搭建独立官网，再谈数字化营销

不少企业一直都在追求数字化转型，嘴上不断说着数字化营销，可最终取得的效果却不尽人意，这是为什么？

当然是因为他们没有搭建自己的独立官网了！先有独立官网，拥有自己的平台后，才能谈如何进行数字化营销。

以自己的独立官网为基础，环绕小程序、APP、视频平台，形成流量闭环，再构建属于自己的数据池，接着才轮到定位营销方案。

通过这一套“组合拳”，中小企业想要翻身，让销售量几何式增长的同时还能满足低成本的要求，这才是中小企业的福音，也是LTD营销SaaS一直坚持的信念。

没有独立网站升级迭代，就没有数字化营销！

而只需要通过LTD营销SaaS，轻松动动手指，不到十分钟便可以搭建一个独立官网，何乐而不为呢？

以嘉瑞国际人力公司（以下简称嘉瑞国际）为例：

通过LTD，嘉瑞国际获得了什么？

嘉瑞国际是一家致力于为全国各类企事业单位及政府部门提供专业的全方位服务的公司。曾几何时，嘉瑞国际也面对着“无人问津”的困境，想要做出改变却无从下手。

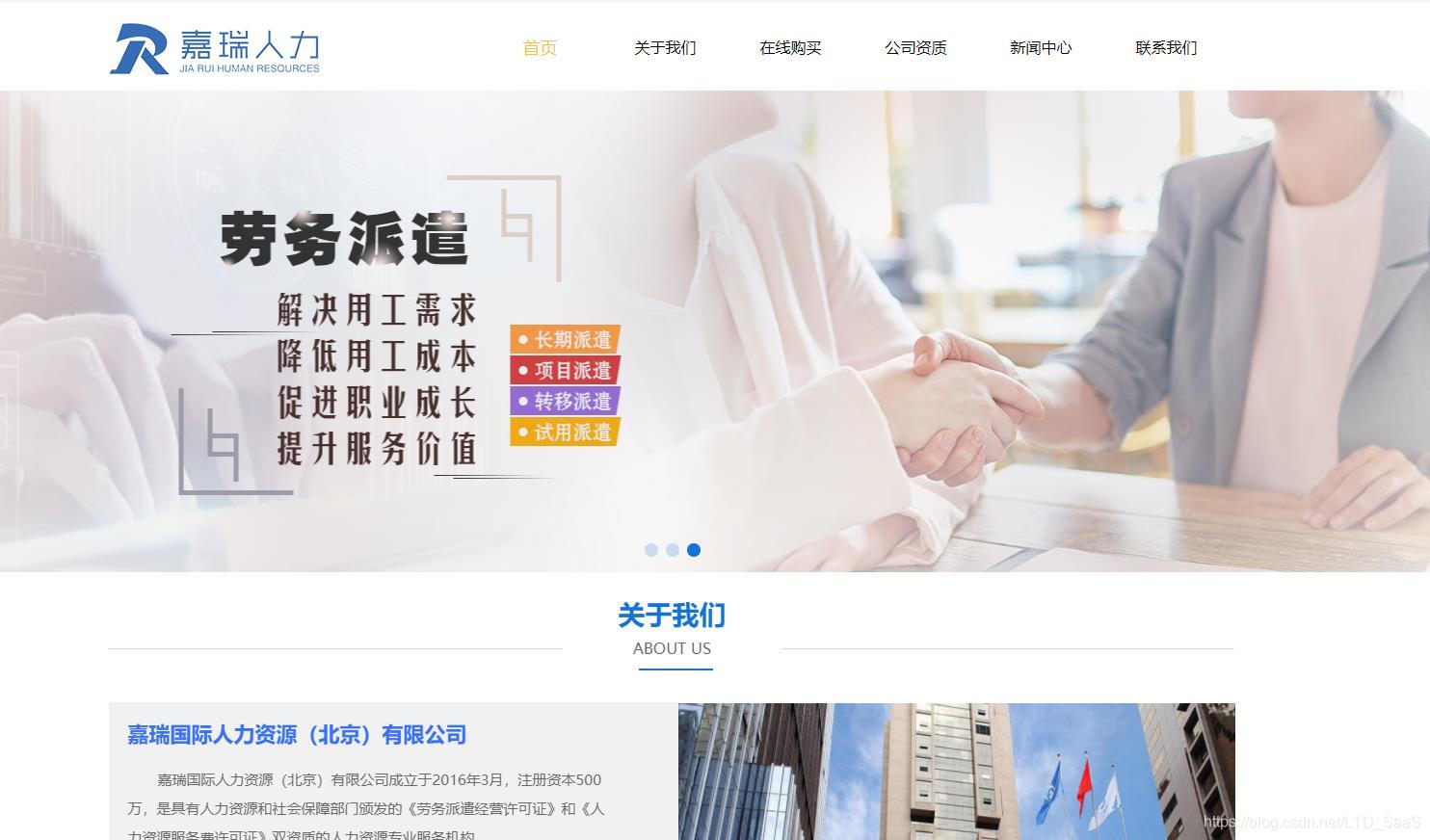
但好在此时他们选择了LTD，通过LTD营销SaaS系统，嘉瑞国际快速搭建了属于自己的社交型独立官网，升级迭代了老套的传统网站，同时利用官微中心后台的推广功能，保持网站的SEO优化，稳定提高搜索引擎排名，进一步增加获客。

树立品牌意识，如何打造品牌知名度是营销过程中不可或缺的一部分，这也意味着打响品牌知名度也是企业营销的目标。

嘉瑞人力通过LTD官微中心，利用后台进行数据管理，数字化营销内容分发，新型官微名片等整合策略，多个获客入口，不放过任何数据转化的可能性。

同时LTD还为嘉瑞国际提供了个性化定制的服务，赢得了多方位全面数字化营销优质结果，规避了传统模式的存在的弊端，让嘉瑞国际零广告成本，实现高质量的获客。

中小企业不能空谈数字化营销，更新迭代自己的官网，也没你想的这么难，选择LTD营销SaaS，成功就在等着你的到来！