网络流问题求解及Gurobi+Python代码（最大流/最小成本网络流/多商品网络流）

本文主要是介绍网络流问题求解及Gurobi+Python代码（最大流/最小成本网络流/多商品网络流），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.最大流问题

1.1 问题描述

1.2 Ford-Fulkerson算法

1.3 Gurobi测试

2.最小成本网络流问题

2.1 问题描述

2.2 供应链规划案例

3.多商品网络流问题

3.1 问题描述及模型

3.2 Gurobi测试

Gurobi求解代码：GitHub - bujibujibiuwang/Network-Flow-Problem: 网络流问题

1.最大流问题

1.1 问题描述

最大流问题（Maximum flow problem MFP）描述为一个有向图，包含源节点（source）和汇点（sink），以及连接这些节点的有向边，每条边都有一个容量，表示通过该边的最大流量。问题优化目标是寻找最大流量传输。如下图所示，该网络的最大流为23。

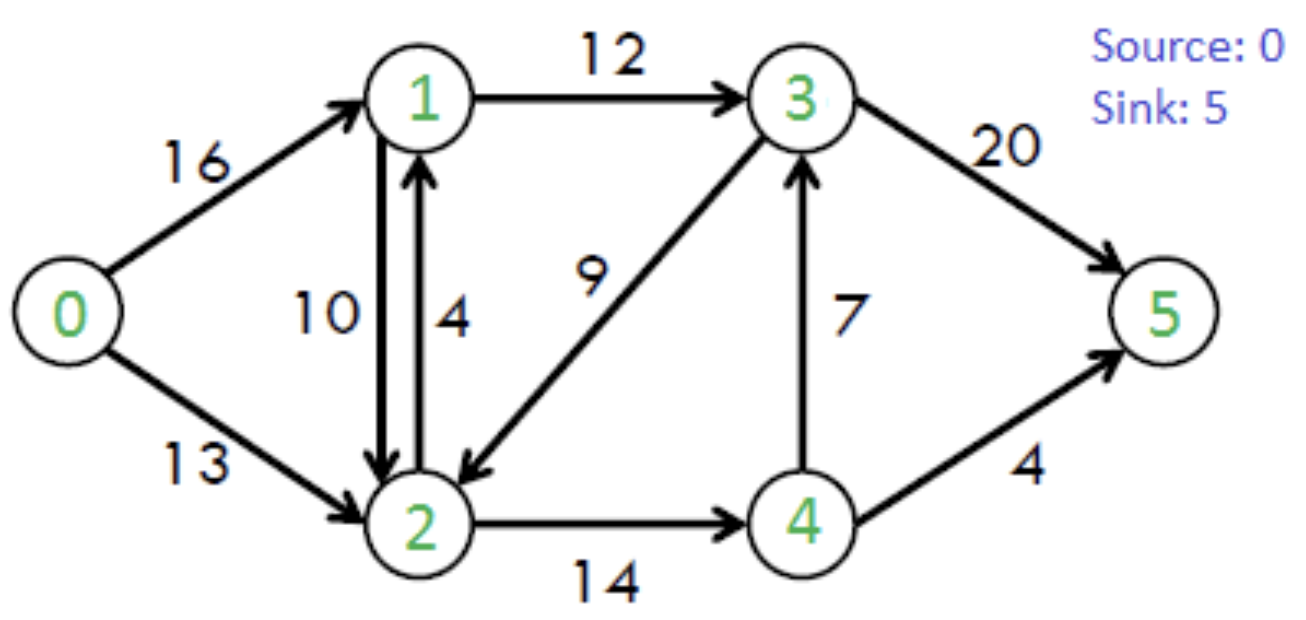
求解最大流问题的方法：

Ford-Fulkerson 算法
求解器

1.2 Ford-Fulkerson算法

定义1

定义2

算法步骤如下：

下面是一个简单例子

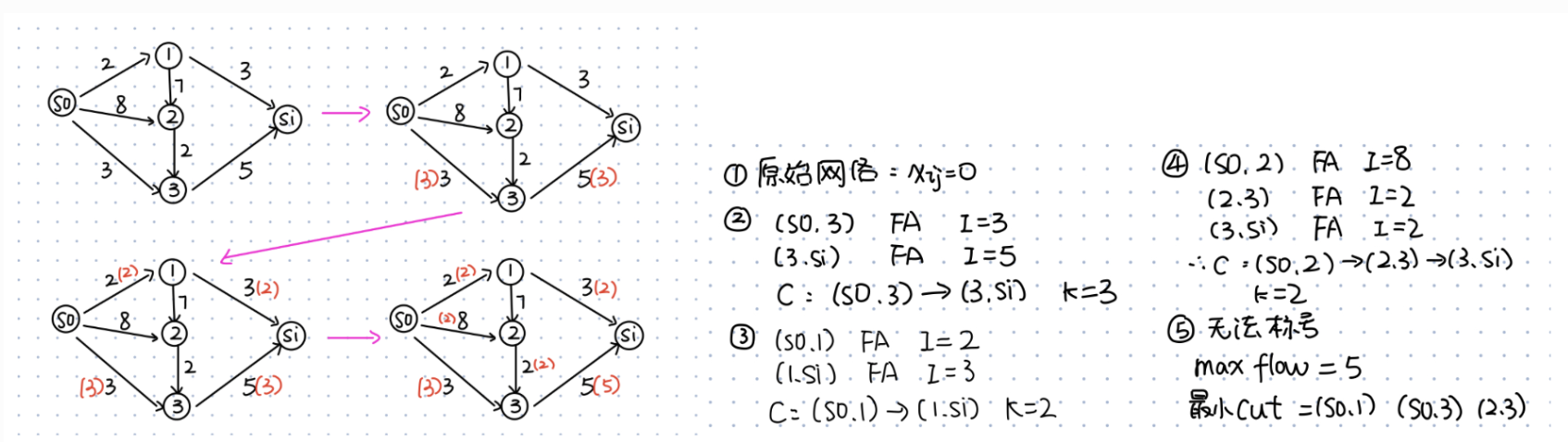
1.3 Gurobi测试

最大流问题有两个约束：流平衡约束和容量约束，模型描述如下：

在一个简单的例子上使用gurobi求解最大流问题，结果如下图，最大流为20

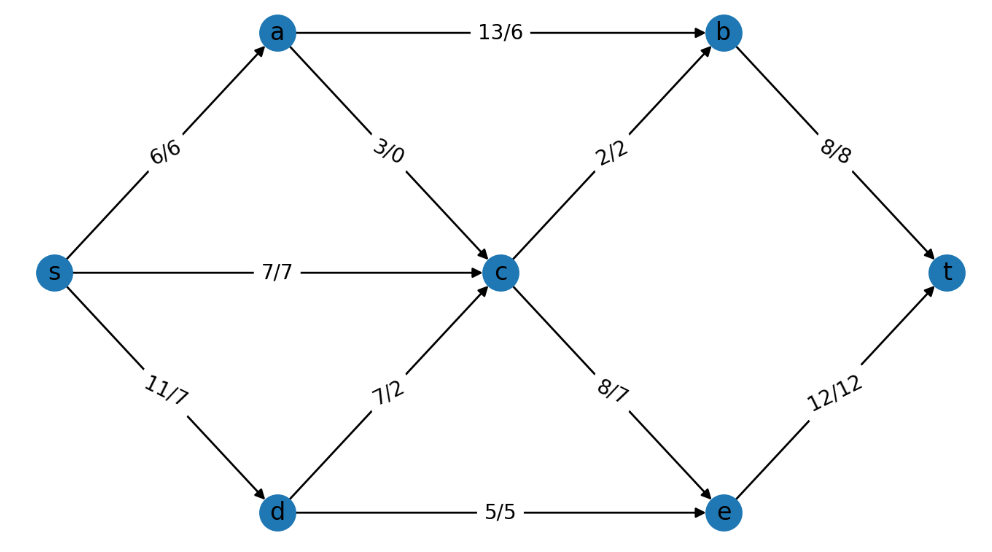
模型核心代码如下：

maxflow = gp.Model()
flow = maxflow.addVars(edges.keys(), vtype=GRB.CONTINUOUS)
maxflow.setObjective(flow.sum('*', 't'), GRB.MAXIMIZE)
maxflow.addConstrs(flow[i, j] <= edges[i, j] for i, j in edges.keys())
maxflow.addConstrs(flow.sum('*', i) - flow.sum(i, '*') == 0 for i in points.keys() if i != 's' and i != 't')
maxflow.optimize()

2.最小成本网络流问题

2.1 问题描述

运输问题，分配问题，转运问题，最短路径，最大流等都属于最小成本网络流问题（Minimum-cost network flow problem MCNFP)，在该问题中，有一个有向图表示网络，其中包含一些节点和边，每条边都有一个容量和一个单位费用。网络中有供应点，需求点，中转点等，最小成本网络流问题的目标是找到一种流量分配方案，使得满足需求的同时，总运输成本最小。

2.2 供应链规划案例

参考gurobi官方资源Supply Network Design 1

供应链网络设计问题可以转化为最小成本网络流问题，具体而言，有6个客户点，4个仓库中心，2个工厂，每个客户点都有已知的需求，客户的需求可以通过仓库或者工厂提供，每个仓库有最大容量限制，每个工厂有最大供应量，已知将产品从工厂运输到仓库、从仓库运输到客户、或从工厂直接运输到客户的成本，要求找到确定满足客户需求的最佳运输方式，同时最大限度地降低运输成本。模型如下：

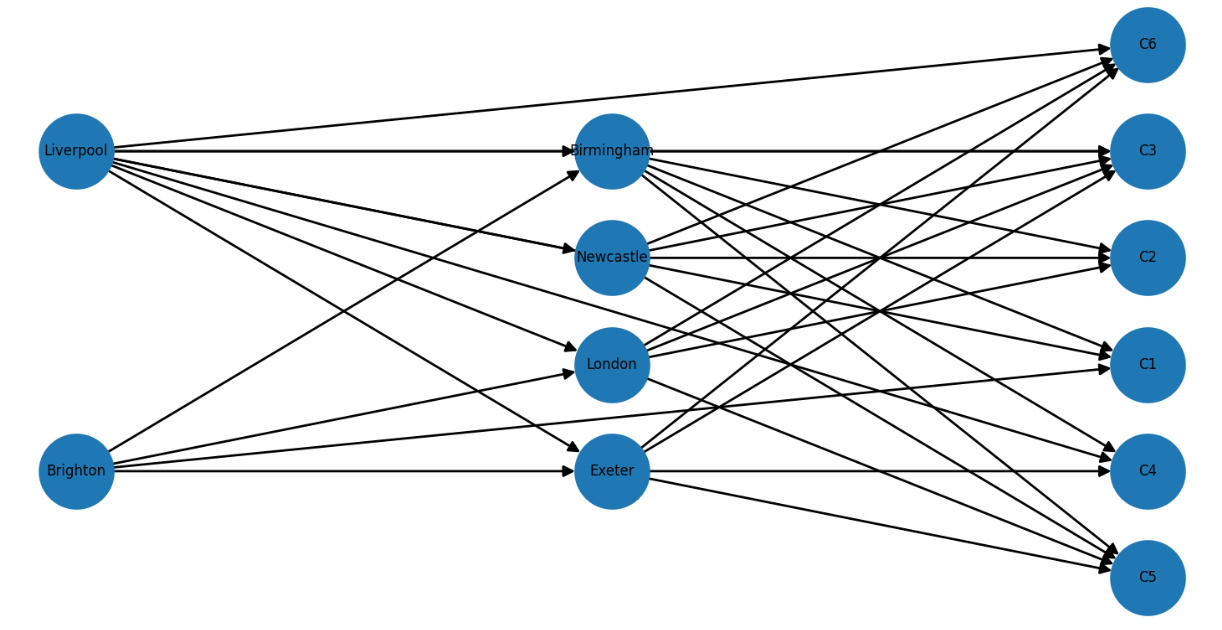
模型核心代码如下：

"""
(1)决策变量和目标函数
"""
cost_flow = gp.Model()
flow = cost_flow.addVars(list(edges), vtype=GRB.CONTINUOUS, name='x')
cost_flow.setObjective(flow.prod(edges), GRB.MINIMIZE)
"""
(2)约束条件
"""
# factory constraints
cost_flow.addConstrs(flow.sum(i, '*') <= factories[i] for i in factories.keys())
# depots constraints
cost_flow.addConstrs(flow.sum(i, '*') <= depots[i] for i in depots.keys())
# customers constraints
cost_flow.addConstrs(flow.sum('*', i) == customers[i] for i in customers.keys())
# flow constraints
cost_flow.addConstrs(flow.sum('*', i) == flow.sum(i, '*') for i in depots.keys())

求解结果如下：

Optimal objective  1.985000000e+05

3.多商品网络流问题

3.1 问题描述及模型

多商品流动问题（Multi-commodity flow problem MCFP）是不同源节点和汇节点之间存在多种商品（流动需求）的网络流动问题。模型如下：

3.2 Gurobi测试

参考multi-commodity-flow

在一个简单的例子上测试，2种商品，5个城市，模型核心代码如下：

"""
(1)变量和目标
"""
multi_commodity = gp.Model()
flow = multi_commodity.addVars(list(cost), vtype=GRB.CONTINUOUS)
multi_commodity.setObjective(flow.prod(cost), GRB.MINIMIZE)
"""
(2)约束条件
"""
# 容量约束
multi_commodity.addConstrs(flow.sum('*', u, v) <= edges[(u, v)] for u, v in edges.keys())
# 流平衡约束
multi_commodity.addConstrs(flow.sum(h, '*', v) + inflow[h, v] == flow.sum(h, v, '*')for h in commodities for v in points.keys())

求解结果如下：