代码随想录算法训练营day 26|第七章 回溯算法part03

本题是集合里元素可以用无数次，那么和组合问题的差别 其实仅在于 startIndex上的控制

题目链接/文章讲解：代码随想录

视频讲解：带你学透回溯算法-组合总和（对应「leetcode」力扣题目：39.组合总和）| 回溯法精讲！_哔哩哔哩_bilibili

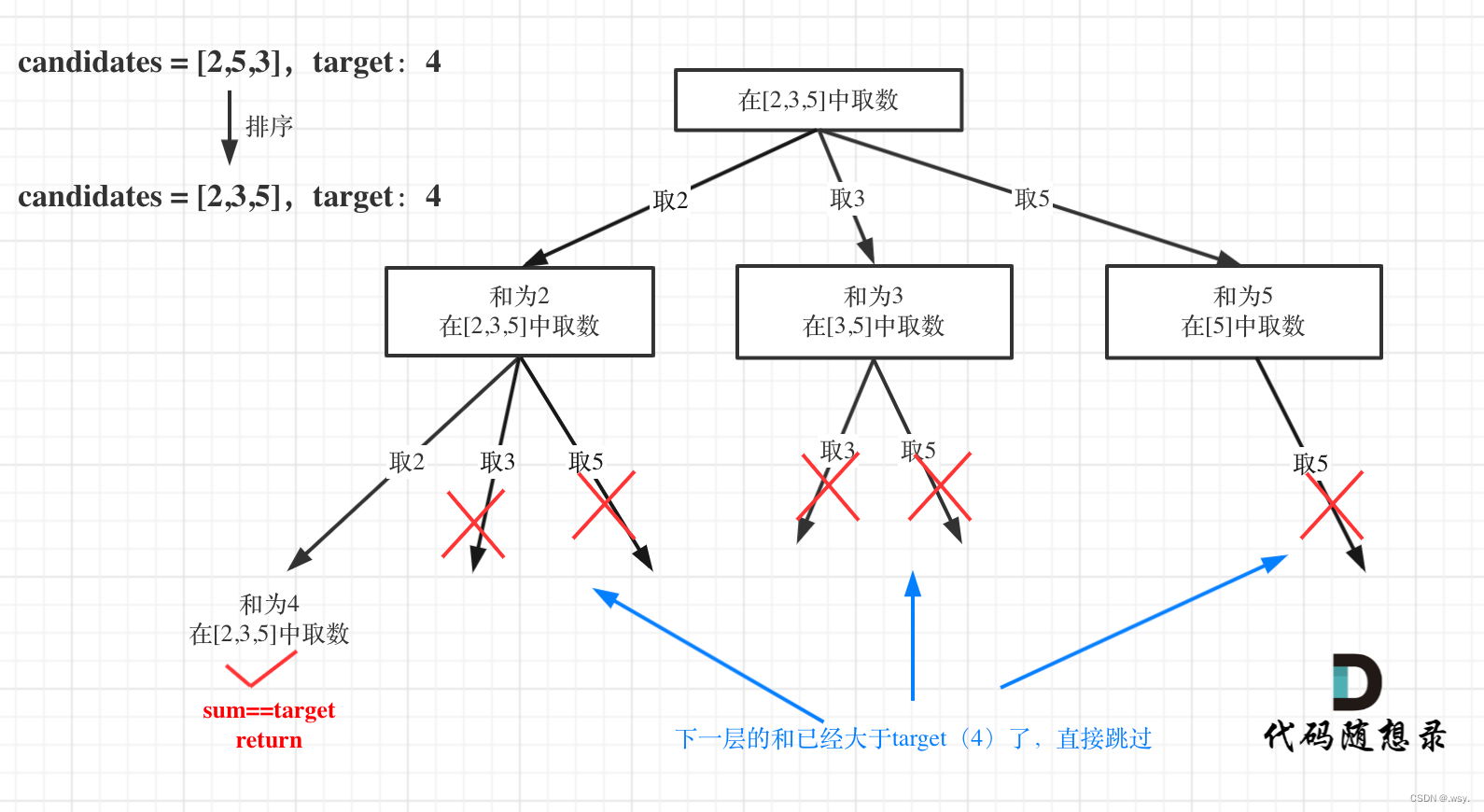
这道题主要的特点是已经选过的数可以重复选取，所以每次选取的数的开始下标就直接是当前下标，这样设置每次选取数字只能选取包括本身在内的剩下的数就可以保证不重复。这道题的剪枝是很典型的，基本上大多数的回溯都需要事先将数组进行排序，然后再进行剪枝，这题就是如此。

class Solution {
public:vector<vector<int>> res;vector<int> path;void backtracking (vector<int>& candidates,int begin,int target){if(target==0){res.push_back(path);return ;}for(int i=begin;i<candidates.size();i++){if(candidates[i]>target) return ;path.push_back(candidates[i]);backtracking(candidates,i,target-candidates[i]);path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());backtracking(candidates,0,target);return res;}
};

40.组合总和II 

本题开始涉及到一个问题了：去重。注意题目中给我们 集合是有重复元素的，那么求出来的 组合有可能重复，但题目要求不能有重复组合。 

题目链接/文章讲解：代码随想录

视频讲解：回溯算法中的去重，树层去重树枝去重，你弄清楚了没？| LeetCode:40.组合总和II_哔哩哔哩_bilibili

这道题主要的难点就是去重，其他的部分和同系列题目基本一致。首先要明确重复数组是怎样产生的，重复是由于之前用过的数字再次出现在数组的同一位置，于是就要保证同一位置也就是同一个for循环中不能出现相同的数字（每一次for循环实际上就是为path数组的当前位置在合适区间中选择一个数）（也就是文章中提到的树层去重），因为之前已经为candidates排过序了，所以相同的数字必然下标相邻，这就大大方便树层去重。接着就是文章所指的树枝去重，意为下一层递归的数字要从当前下标之后的剩下的数字中选择，因为考虑的是下一步的情况，所以叫树枝去重。

class Solution {
public:vector<vector<int>> res;vector<int> path;void backtracking(vector<int>& candidates,int begin,int target){if(target==0){res.push_back(path);return ;}for(int i=begin;i<candidates.size();i++){if(candidates[i]>target) return;if(i>begin&&candidates[i]==candidates[i-1]) continue;path.push_back(candidates[i]);backtracking(candidates,i+1,target-candidates[i]);path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());backtracking(candidates,0,target);return res;}
};

131.分割回文串  

本题较难，大家先看视频来理解 分割问题，明天还会有一道分割问题，先打打基础。 

代码随想录

视频讲解：带你学透回溯算法-分割回文串（对应力扣题目：131.分割回文串）| 回溯法精讲！_哔哩哔哩_bilibili

文章里面的做法是直接将每一段是否是回文字符串求出来，这样每次for循环判断是否回文的时候就会方便很多，如果是回文那就调用递归函数接着在剩下的字符里面挑出回文字符串，如此反复直到找完整个字符串。

其中的关键步骤是求字符串的任意一段是否构成回文。首先要创建好合适的空间（二维数组），因为只有空间一定的时候才方便使用for循环、下标来表达；然后逐一填充二维数组，外层循环是起始下标，内层是结束下标（结束下标要>=起始下标才有意义），注意是要倒着填充的，因为前面的判断可以直接引用后面的判断；如果只有一个元素（起始下标就是结束下标），直接设置为true，如果有两个元素（下标差一），判断二者是否相等即可，如果不止两个元素，那就判断两边元素是否相同&&内部字符串是否回文（这部分属于对之前填充的数组的引用，因为i倒着走的，所以已经填充过了）。

class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome[startIndex][i]) {   // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {                                // 不是回文，跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程，弹出本次已经添加的子串}}void computePalindrome(const string& s) {// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小for (int i = s.size() - 1; i >= 0; i--) { // 需要倒序计算, 保证在i行时, i+1行已经计算好了for (int j = i; j < s.size(); j++) {if (j == i) {isPalindrome[i][j] = true;}else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}}}}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();computePalindrome(s);backtracking(s, 0);return result;}
};

这是我的做法，要比上面的做法要满一些，毕竟是边判断是否回文，边走回溯的，但是很好理解。主要是一旦for循环走到和begin下标处的字符相等的地方，就直接暴力判断是否回文，如果回文再进行下一步。除了暴力判断，还可以再写一个函数来判断，使用一层for循环就可。

class Solution {
public:vector<vector<string>> res;vector<string> path;void backtracking(string s,int begin){if(begin==s.size()){res.push_back(path);return;}string ss,cons;for(int i=begin;i<s.size();i++){if(s[i]==s[begin]){ss=s.substr(begin,i-begin+1);cons=ss;reverse(cons.begin(),cons.end());if(ss!=cons) continue;path.push_back(ss);backtracking(s,i+1);path.pop_back();}}}vector<vector<string>> partition(string s) {backtracking(s,0);return res;}
};

注意关键函数——

string str=s.substr(起始下标,结束下标); //分割字符串
reverse(起始下标,结束下标); //反转字符串