本文主要是介绍Python实现单因素方差分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Python实现单因素方差分析
1.背景
正念越来越受到人们关注，正念是一种有意的、不加评判的对当下的注意觉察。可以通过可以通过观呼吸、身体扫描、正念饮食等多种方式培养。
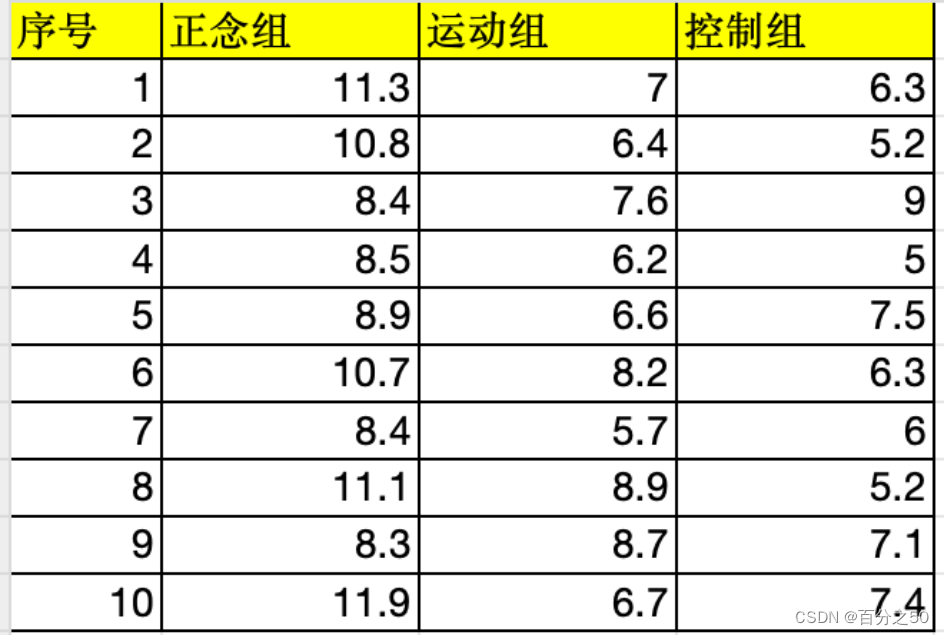
为了验证正念对记忆力的影响，选取三组被试分别进行正念训练，运动训练和无训练，以测量他们的短时记忆是否改善。在各种条件严格控制下，三个月后测量各组的短时记忆回忆容量，结果如下：
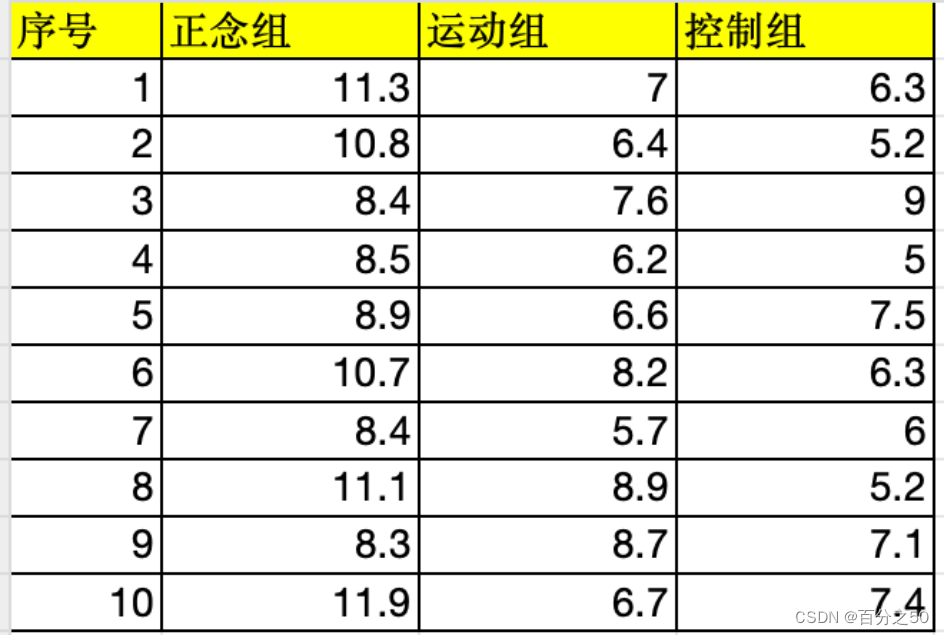
为了验证各组是否存在差异，采用单因素方差分析进行分析，并同时使用SPSS对每一步代码进行说明。
PS：此处为随机数生成，且为了方便展示使用了宽数据，导入SPSS时可使用“数据”-“重构”转换为SPSS常用的长数据。
2.Python代码
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.stats.multicomp import pairwise_tukeyhsd # 事后比较
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lmindependent = "处理" # 自变量
dependent = '短时记忆回忆成绩' # 因变量# 设置画图参数
def define_plt():plt.rcParams['font.sans-serif'] = ['SimHei', ] # 设置汉字字体plt.rcParams['font.size'] = 12 # 字体大小plt.rcParams['axes.unicode_minus'] = False # 正常显示负号# 处理数据
def general_data():# 使用melt（）函数将读取数据进行结构转换，以满足ols（）函数对数据格式的要求，# melt（）函数能将列标签转换为列数据excel_data = pd.read_excel('不同正念处理下的短时记忆成绩.xlsx', index_col=0)melt_data = excel_data.melt(var_name=independent, value_name=dependent)print("\n=================melt_data========================")print(melt_data)return melt_data# 显示箱型线，检查是否有极端数值
def show_boxplot(melt_data):sns.boxplot(x=independent, y=dependent, data=melt_data)plt.show() # 需要放最后运行，否则会阻挡后面程序的运行# 方差分析
def anova(melt_data):# ols（）创建一线性回归分析模型model_ols = ols('%s~C(%s)' % (dependent, independent), melt_data).fit()# anova_lm（）函数创建模型生成方差分析表anova_table = anova_lm(model_ols, typ=2)print("\n=================以下为方差分析表====================")print(anova_table)# 事后比较
def multiple_comparisons(melt_data):# 进行事后比较分析print("\n=================事后比较分析结果====================")print(pairwise_tukeyhsd(melt_data[dependent], melt_data[independent]))define_plt() # 定义plt参数
memory_result = general_data() # 生成数据
anova(memory_result) # 方差分析
multiple_comparisons(memory_result) # 事后比较
show_boxplot(memory_result) # 显示箱型线
3.结果
3.1 运行以上代码，会出现如下结果
3.3.1 方差分析输出结果
对比一下SPSS的输出结果：
英文版
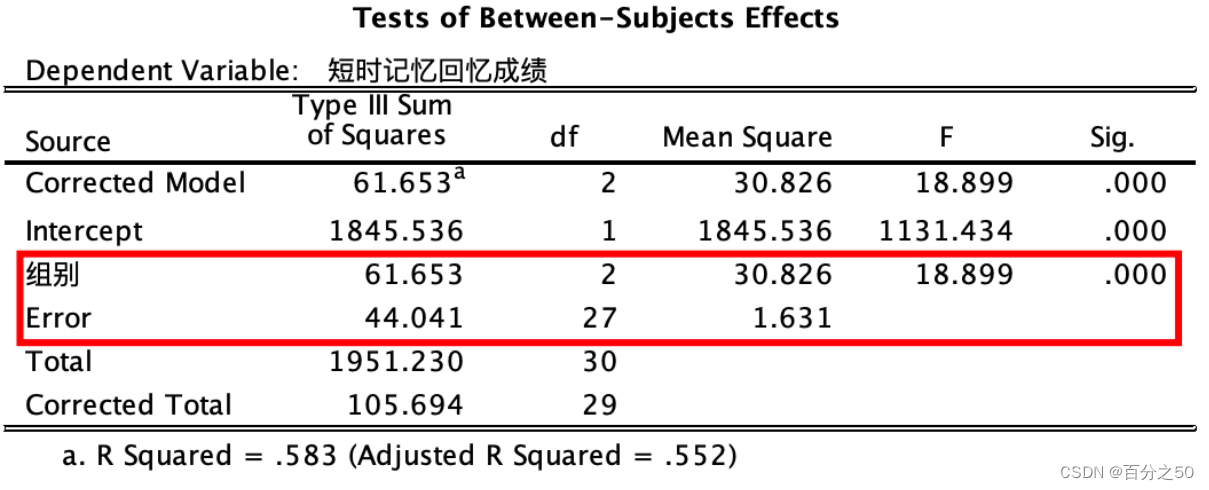
中文版
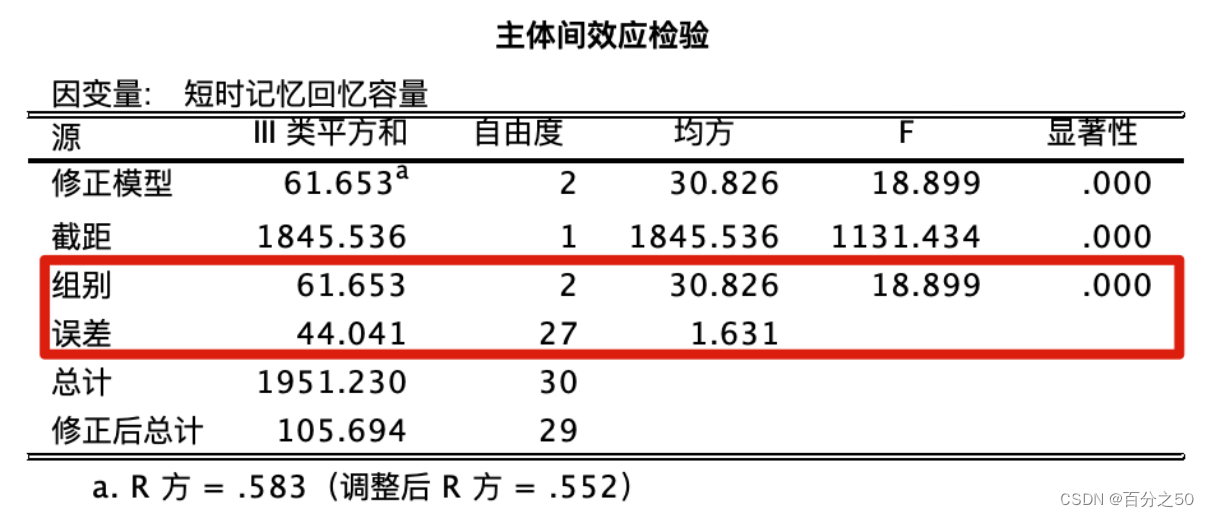
可以看出，Python的输出结果比较简洁，不过其实组别和误差两项也够用了。
3.3.2 事后比较分析结果
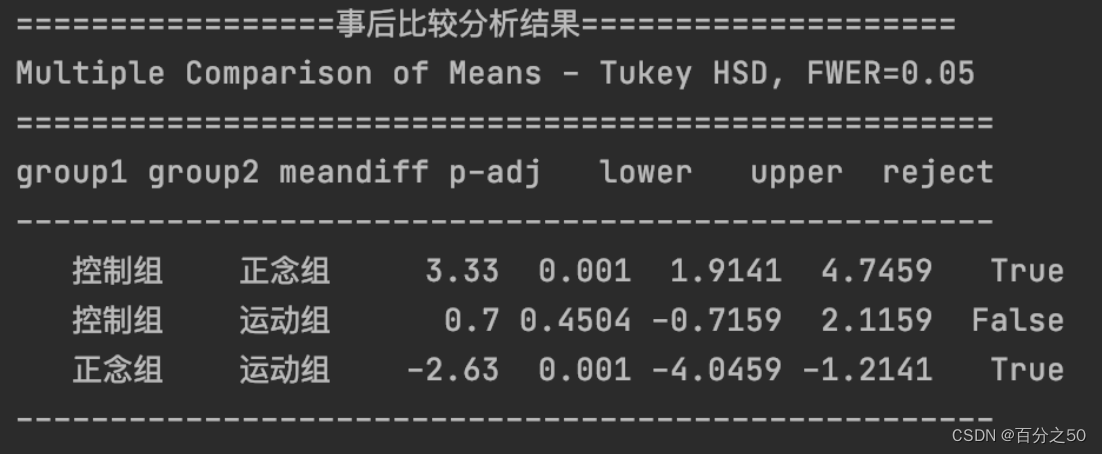
和SPSS中的结果进行比较：
英文版：
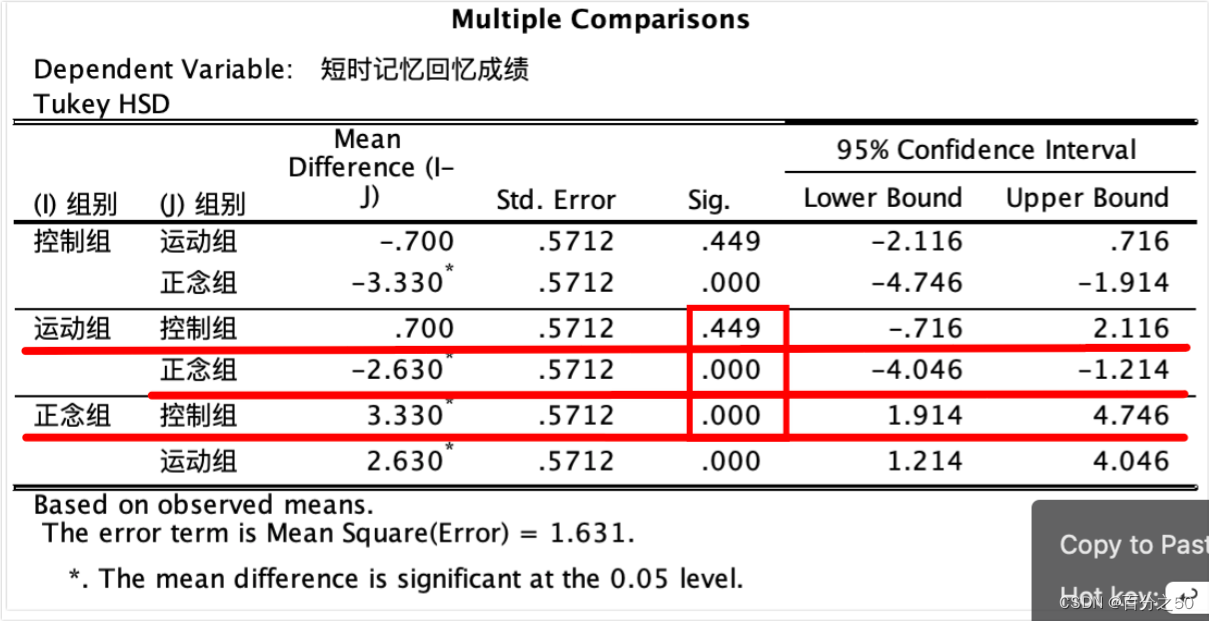
中文版：
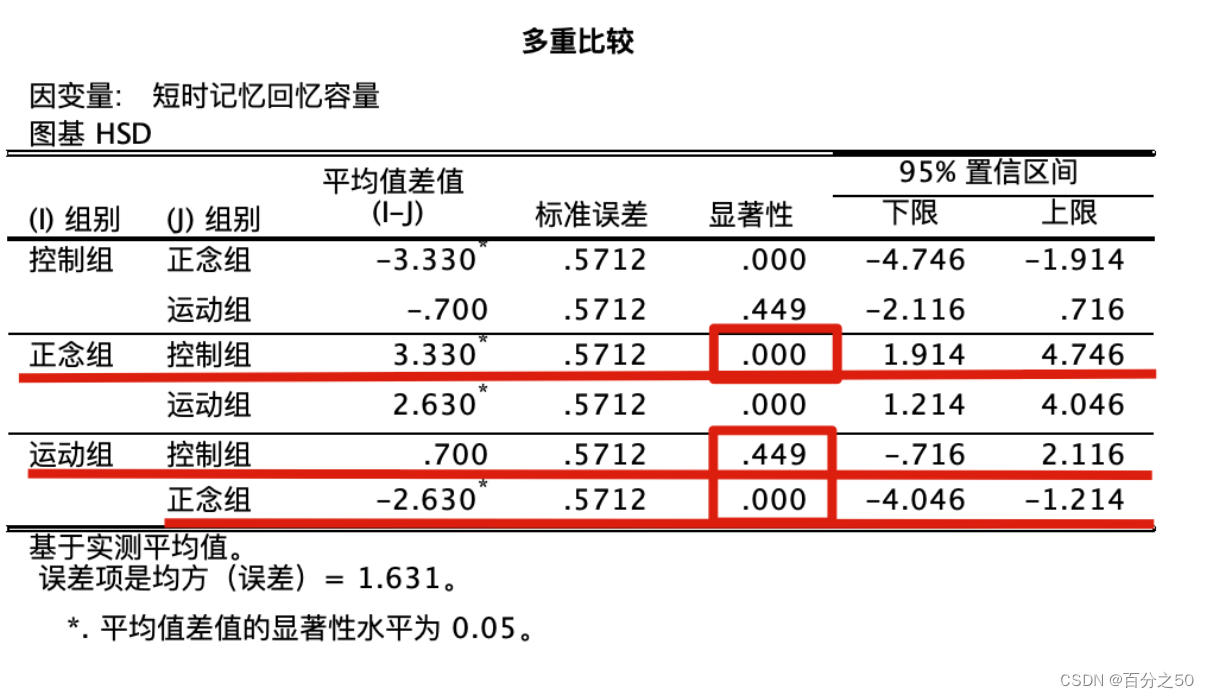
可以看出，Python也是只输出了三个组的对比，不过和SPSS相比，也只是反过来用负数表示而已，重点关注画框的地方，大于0.05说明不能拒绝零假设，Python输出结果则是用False表示。
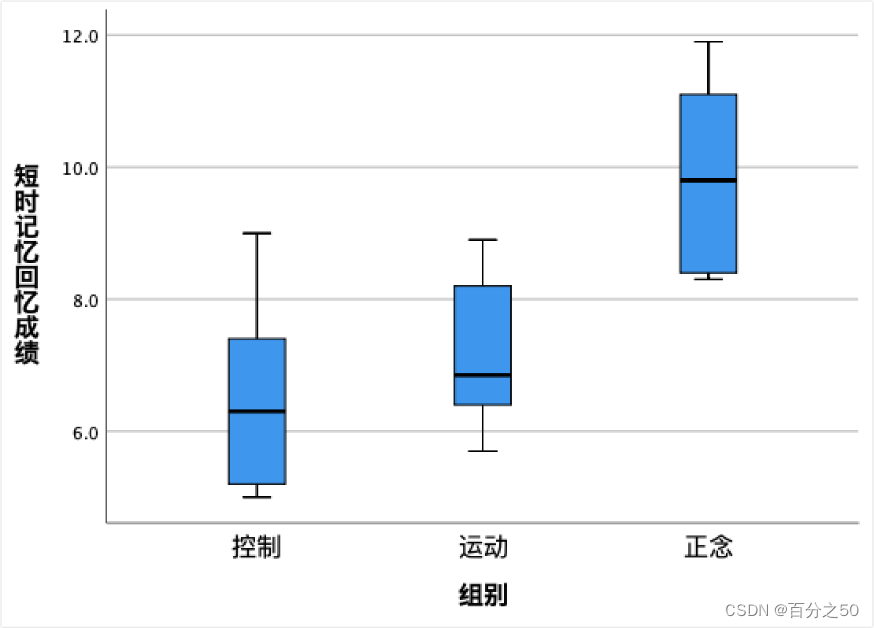
3.3.3 箱型图
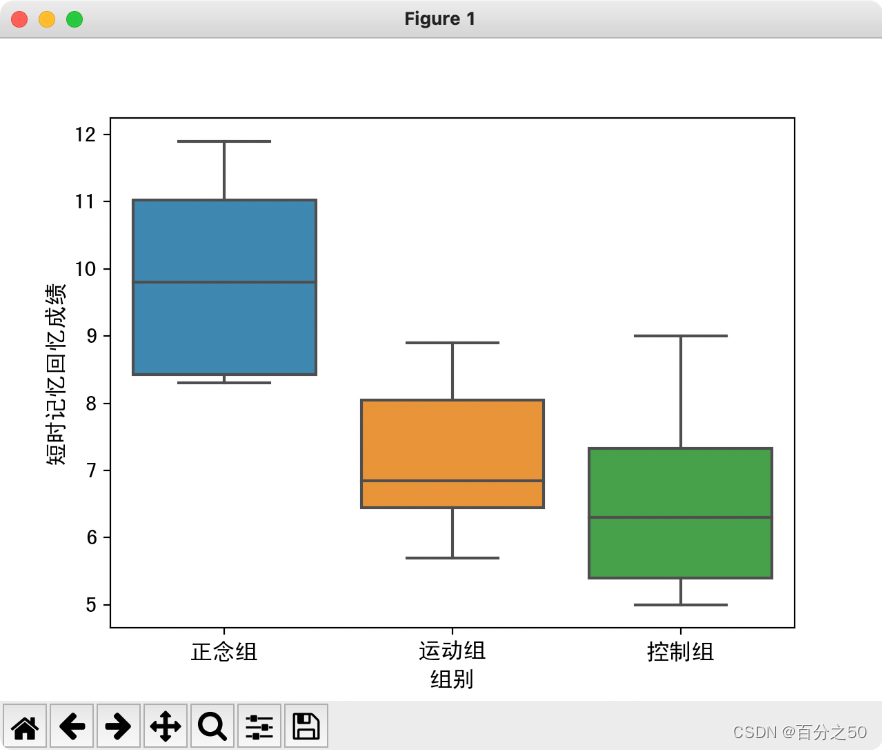
SPSS的输出结果：
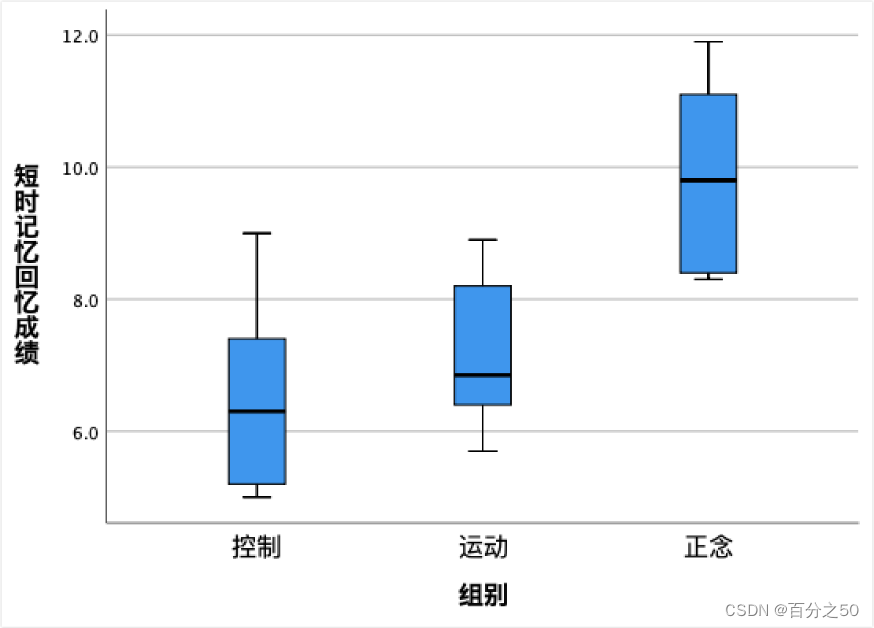
PS：部分字的内容不一样是我在不同地方输入变量的问题，这个无关紧要。
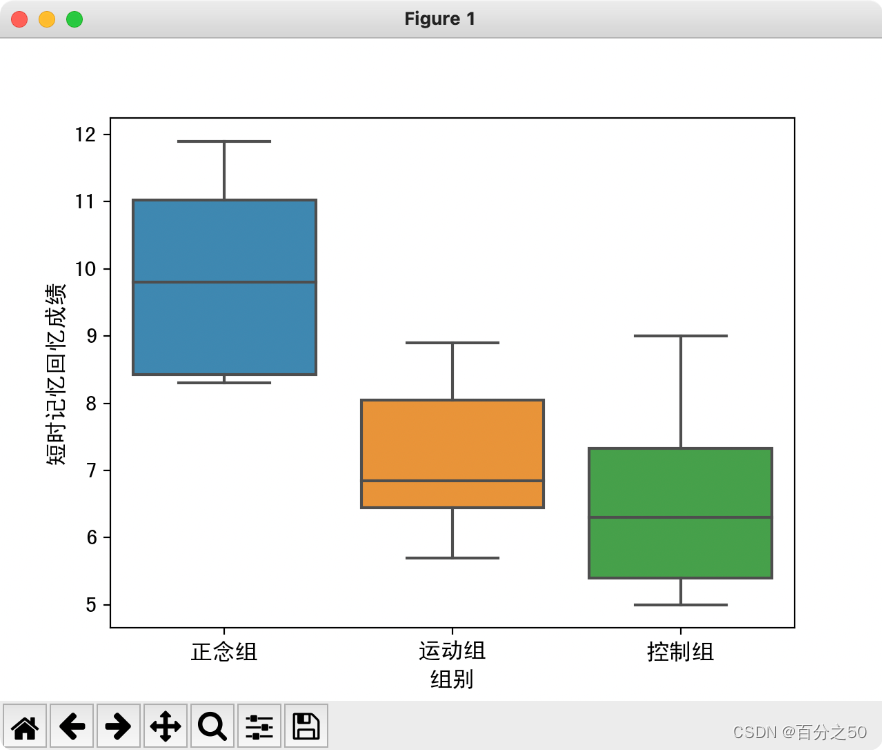
可以看到正念组是明显高于其他两个组的。
箱型图怎么看
箱型图的基本组成部分包括：
1.上边缘：数据点的最右侧界限，通常是最大值。
2.下边缘：数据点的最左侧界限，通常是最小值。
3.中位数：所有数据点按照大小顺序排列后位于中间位置的数值。
4.四分位距：IQR（Interquartile Range，四分位间距）定义为中位数与第一四分位数之间的距离的一半。
5.异常值：那些明显偏离数据集整体趋势的数据点，通常用圆点表示。
箱型图一般不包括均值。
4.逐个部分讲解
4.1 宽数据转换为长数据
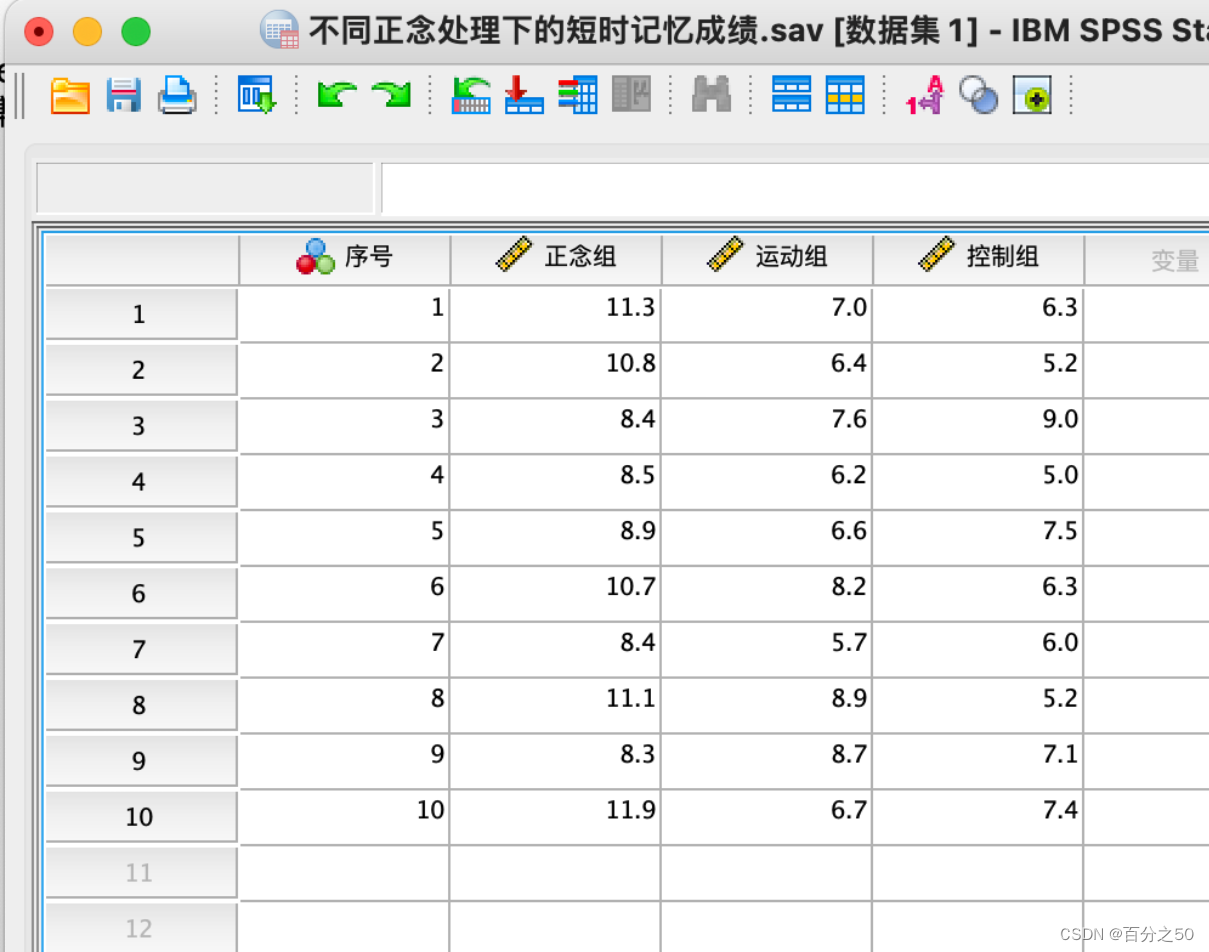
当我们把这张Excel表导入SPSS时，
会显示如下
而我们要将其转换为长数据，即每个列为一个变量的类型
4.1.1 Python代码
在Python代码中，使用melt（）函数实现
# 处理数据
def general_data():# 使用melt（）函数将读取数据进行结构转换，以满足ols（）函数对数据格式的要求，# melt（）函数能将列标签转换为列数据excel_data = pd.read_excel('不同正念处理下的短时记忆成绩.xlsx', index_col=0)melt_data = excel_data.melt(var_name=independent, value_name=dependent)print("\n=================melt_data========================")print(melt_data)return melt_data
我们将输出结果打印出来，如下
=================melt_data========================处理 短时记忆回忆成绩
0 正念组 11.3
1 正念组 10.8
2 正念组 8.4
3 正念组 8.5
4 正念组 8.9
5 正念组 10.7
6 正念组 8.4
7 正念组 11.1
8 正念组 8.3
9 正念组 11.9
10 运动组 7.0
11 运动组 6.4
12 运动组 7.6
13 运动组 6.2
14 运动组 6.6
15 运动组 8.2
16 运动组 5.7
17 运动组 8.9
18 运动组 8.7
19 运动组 6.7
20 控制组 6.3
21 控制组 5.2
22 控制组 9.0
23 控制组 5.0
24 控制组 7.5
25 控制组 6.3
26 控制组 6.0
27 控制组 5.2
28 控制组 7.1
29 控制组 7.4
4.1.2 对应的SPSS操作
为了适应使用不同语言的场景，我将同时呈现中文版和英文版
1.数据-重构
2.将选定变量重构为个案(C）
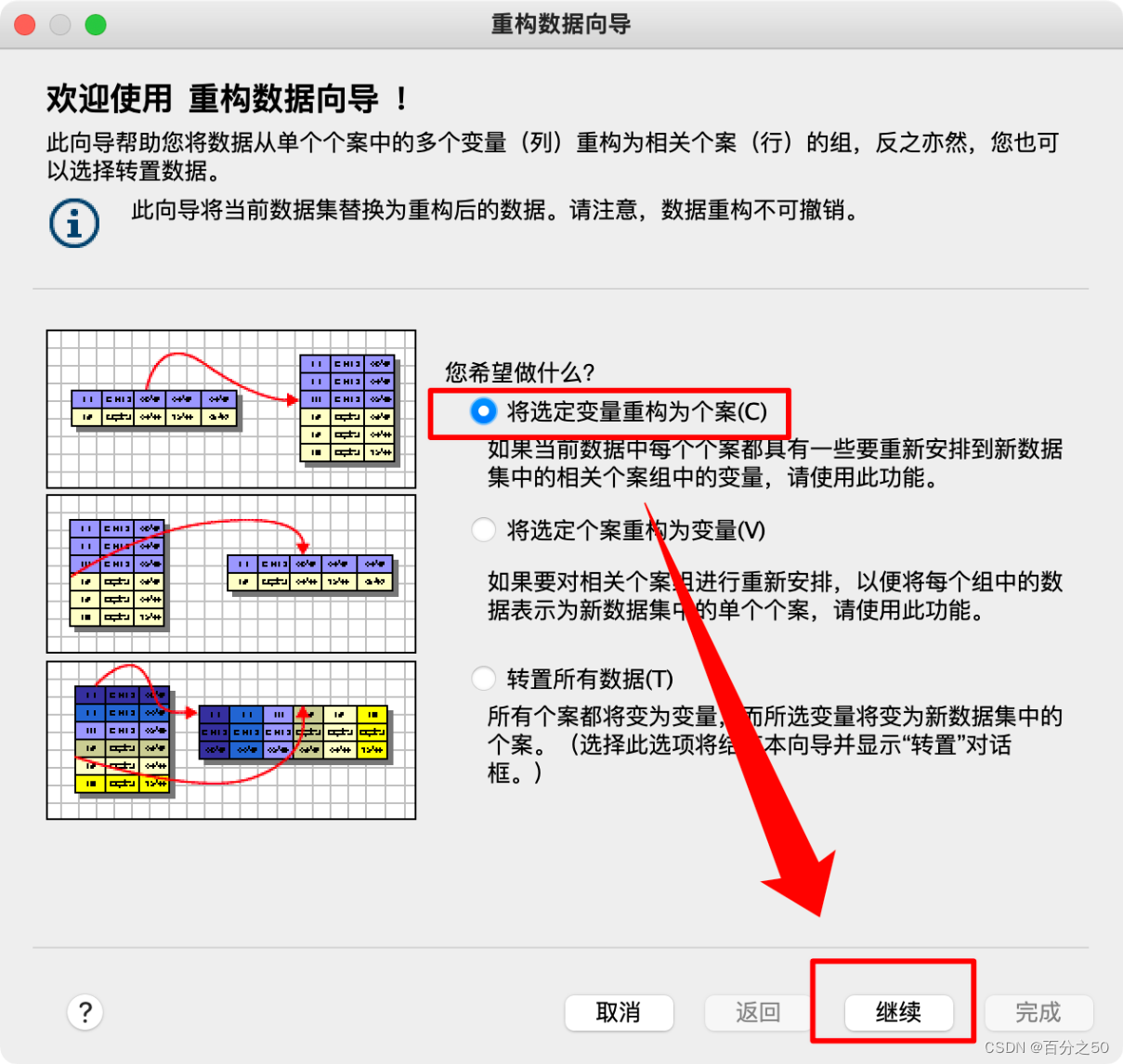
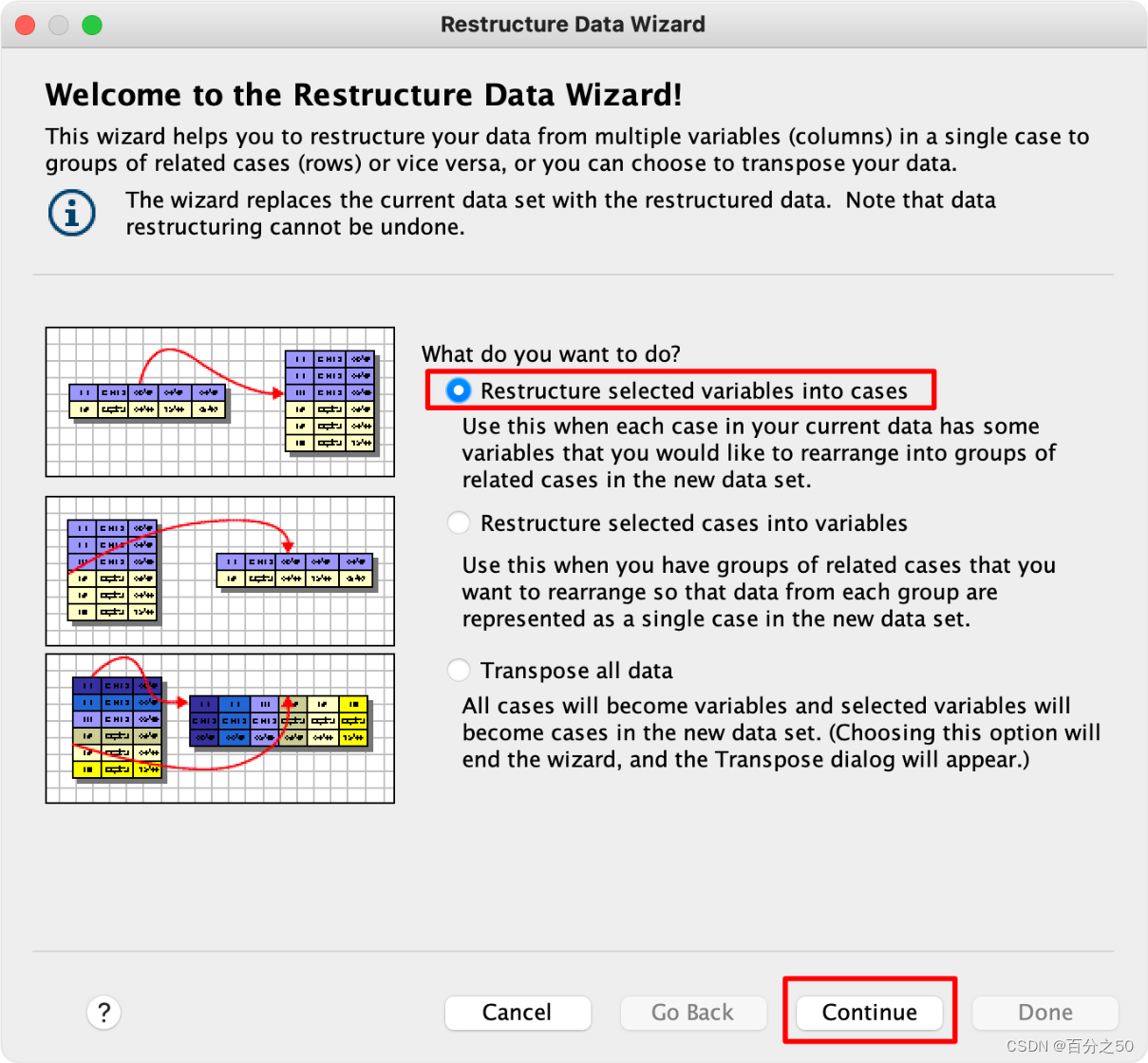
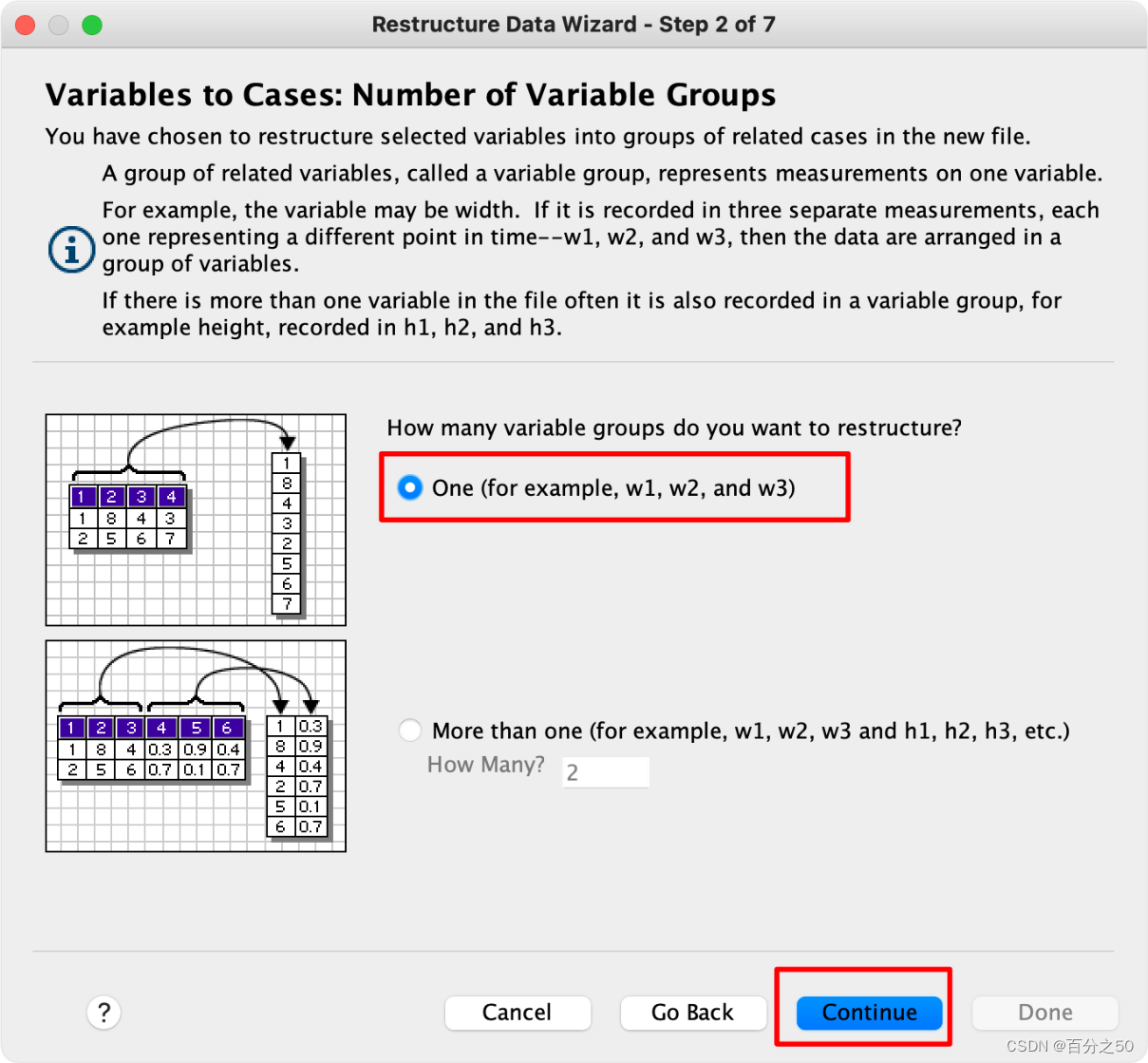
3.重构一个变量组
4.把数据列都放入目标变量中，个案组标识和固定变量可以先不管
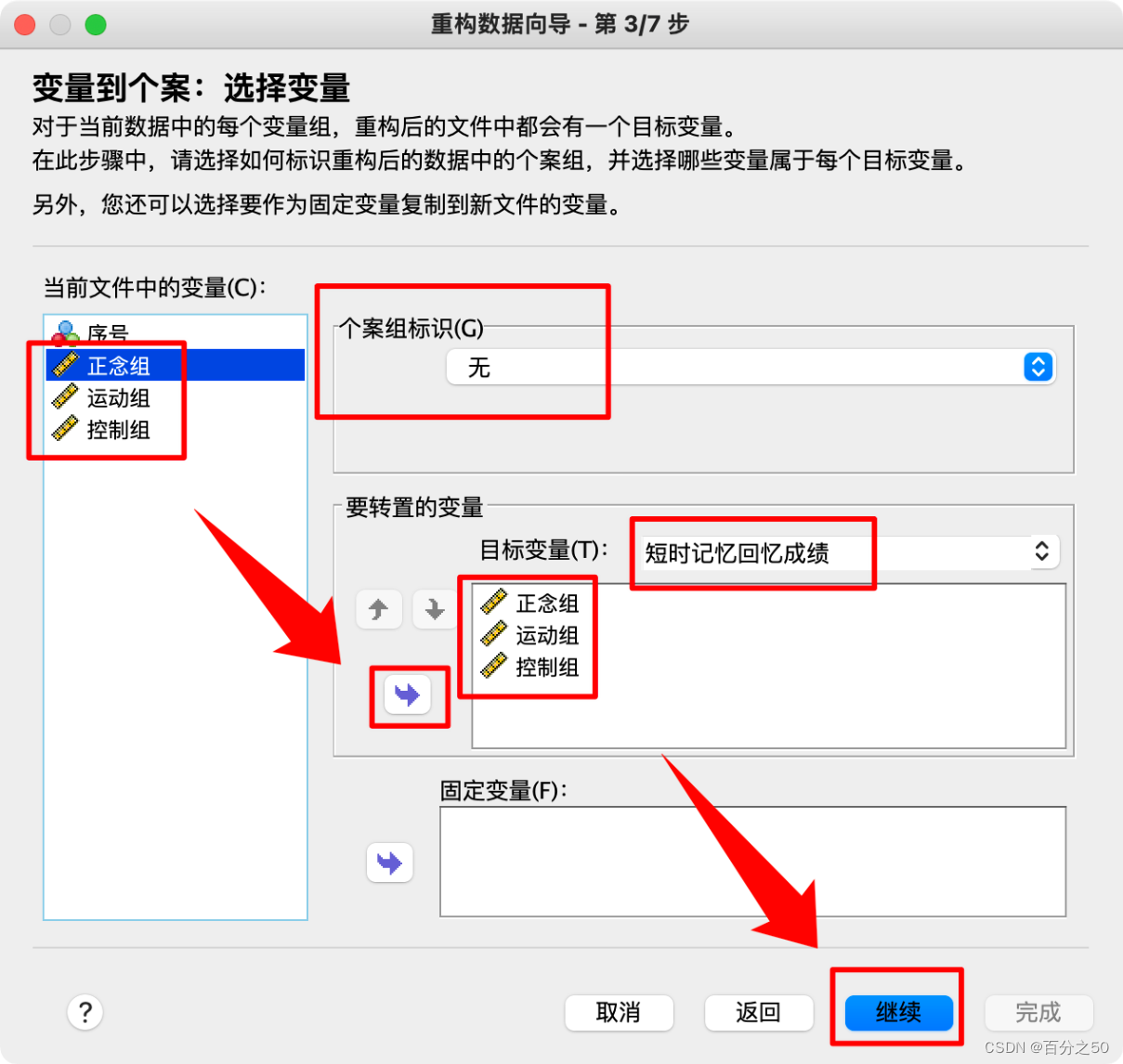
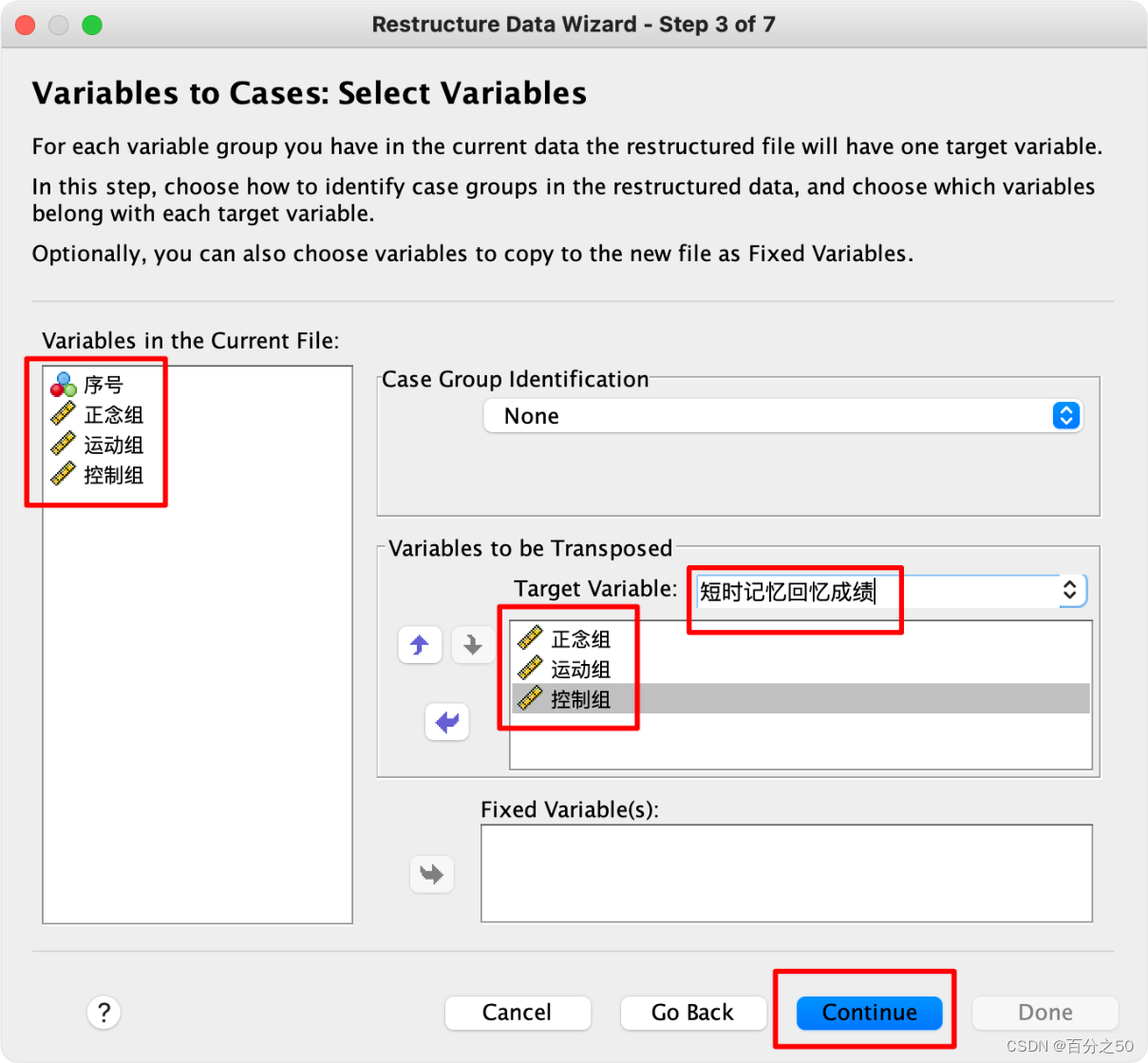
5.这一步将各组名作为索引变量
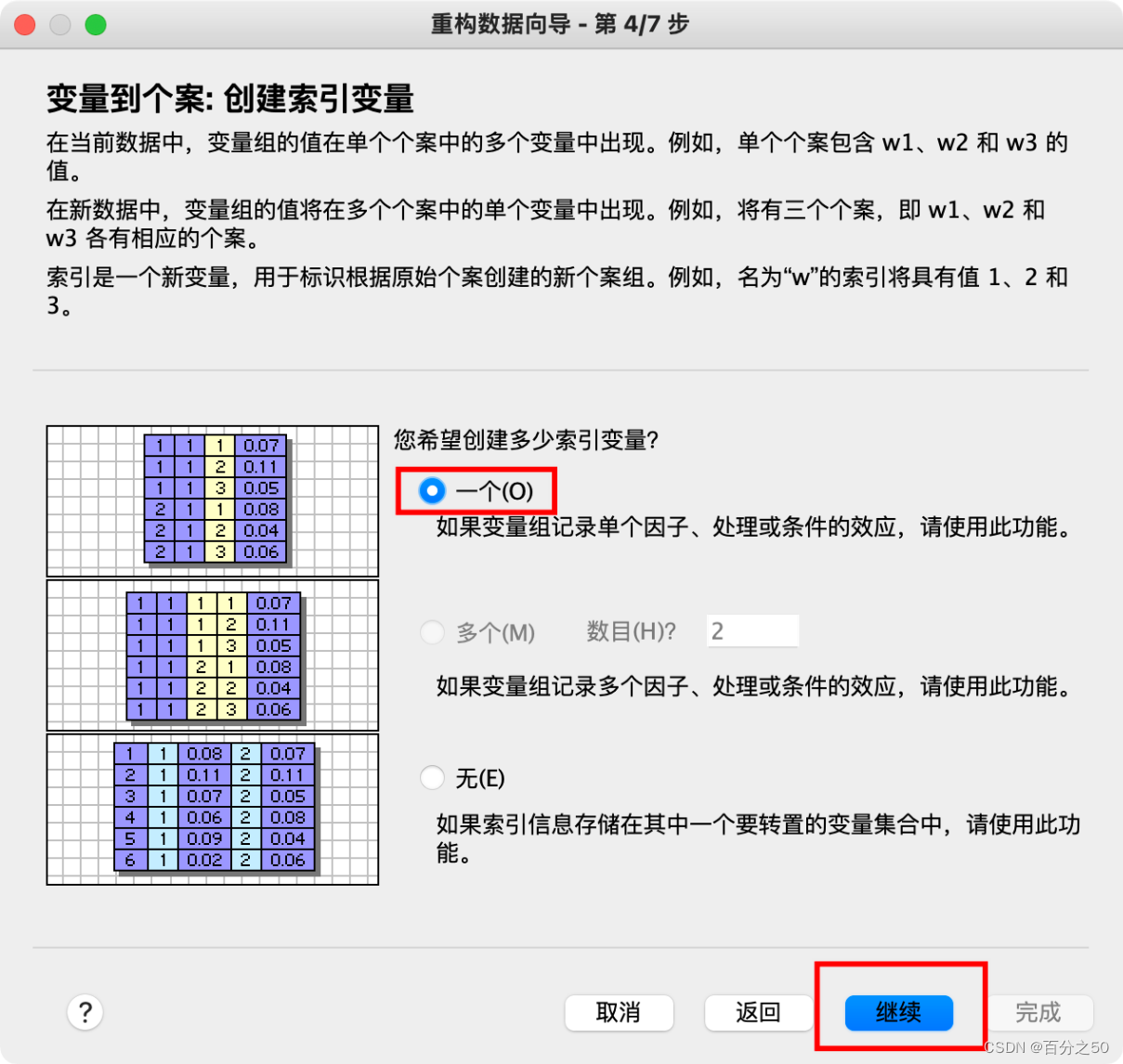
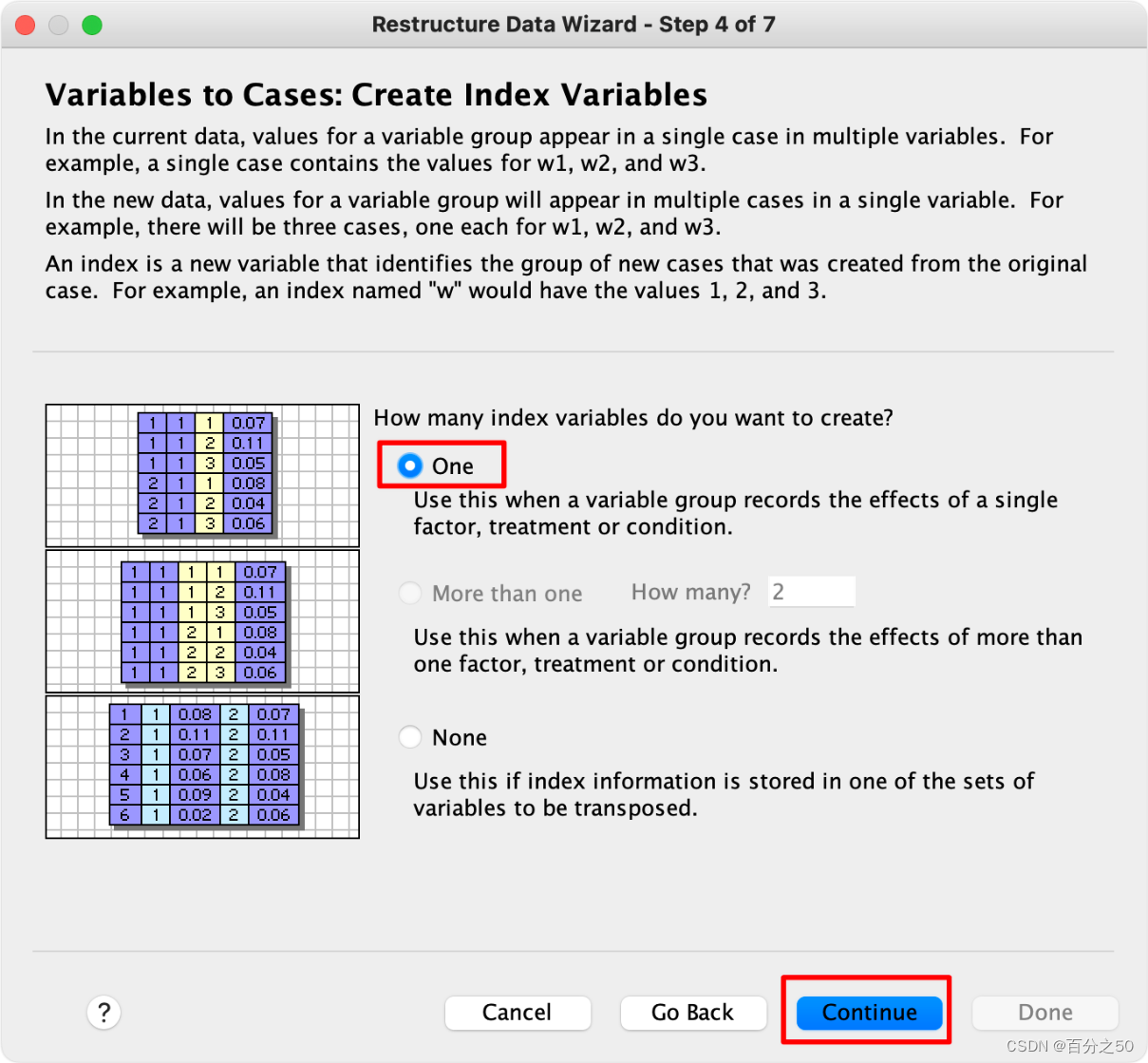
6.选择使用变量名作为索引
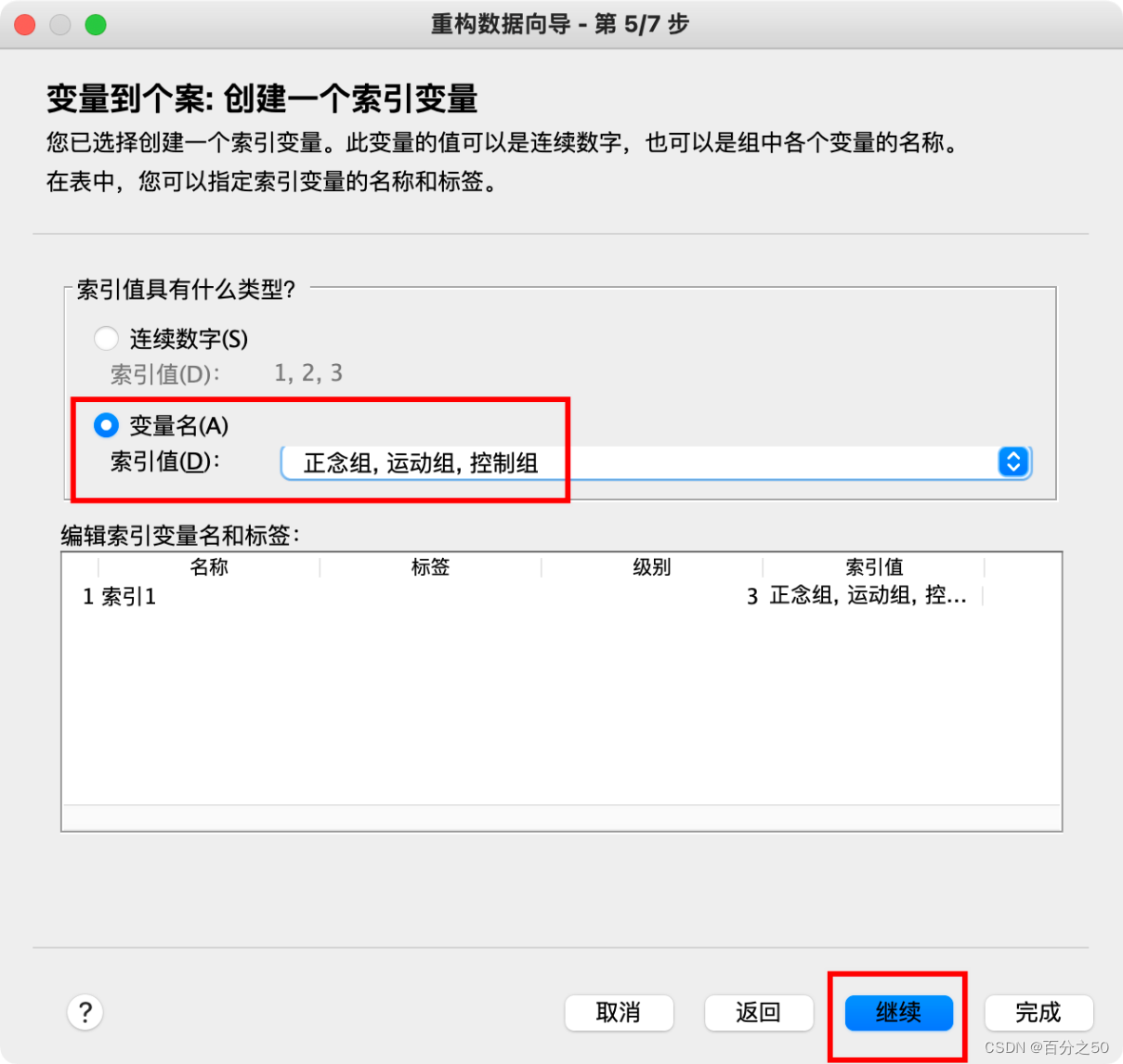
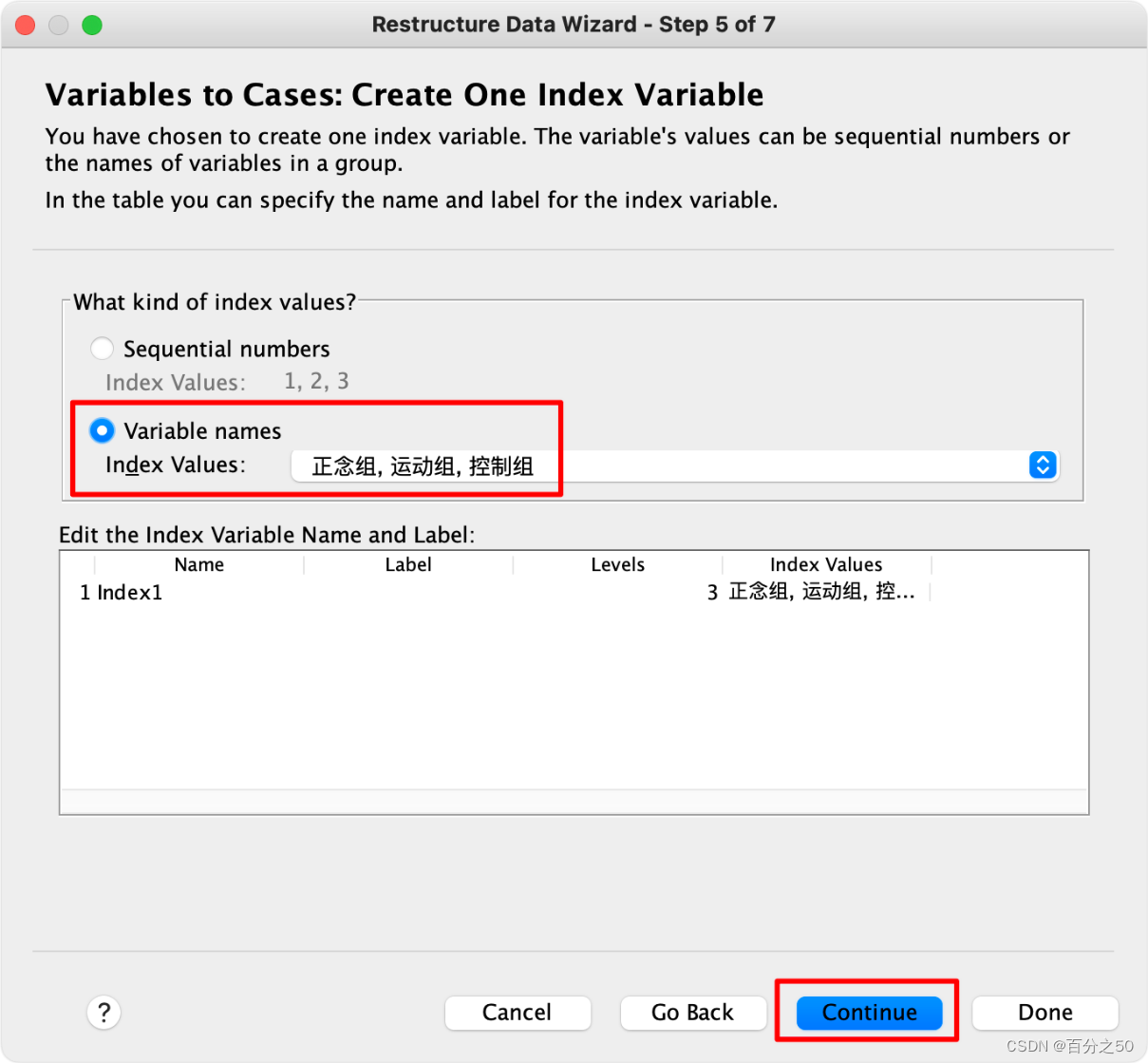
7.之前那个序号没什么用，可以直接删除
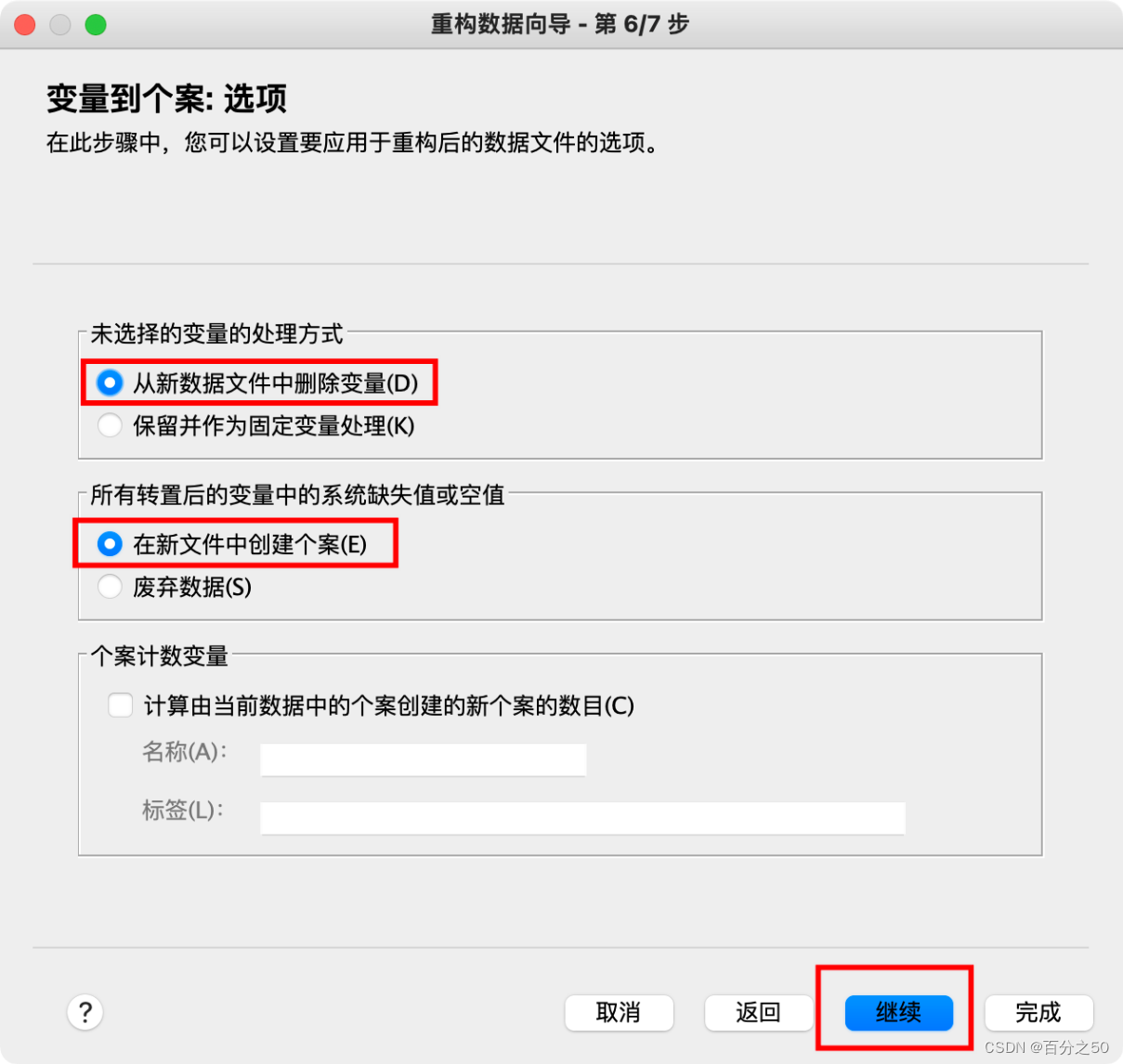
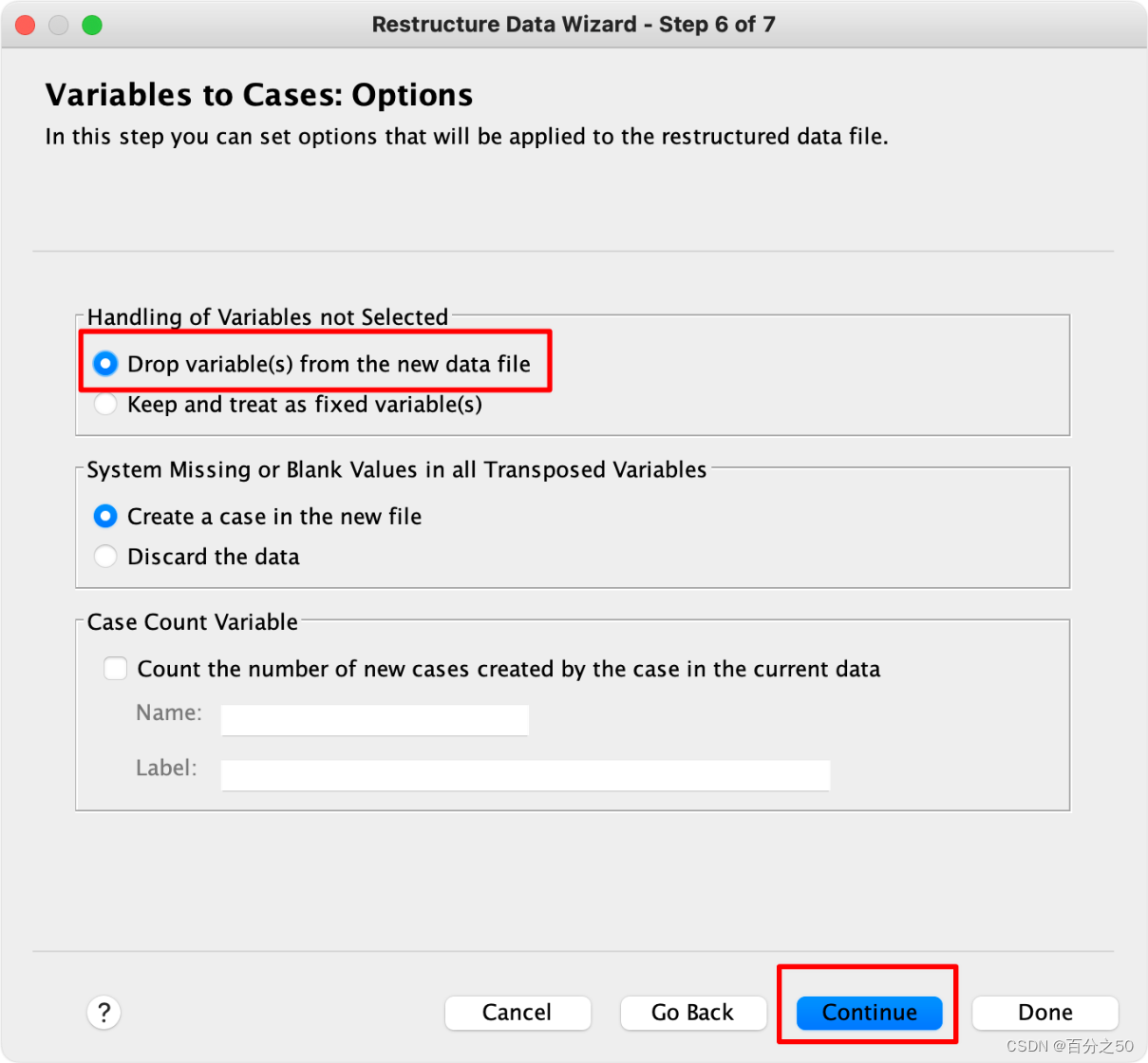
8.完成即可
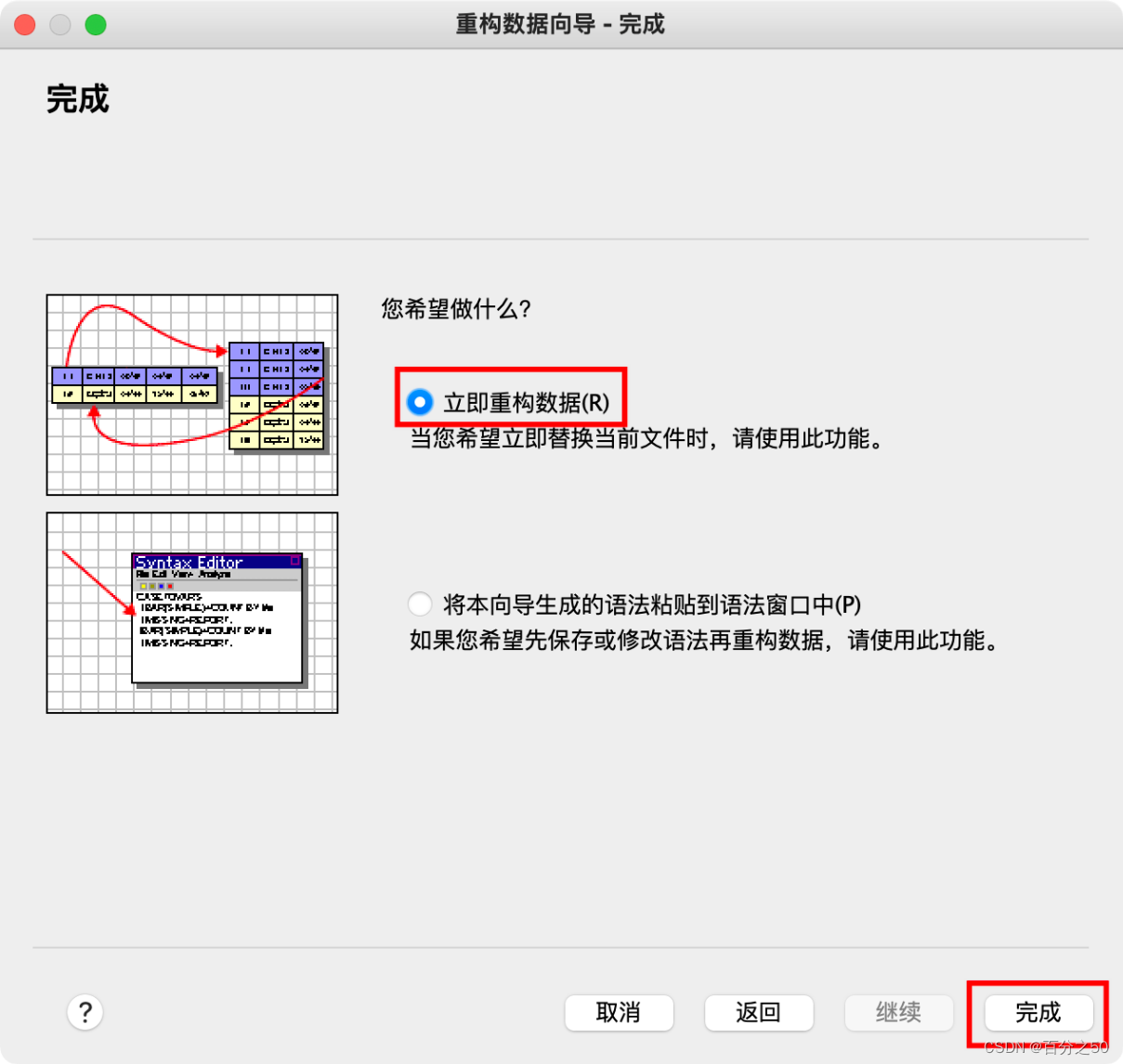
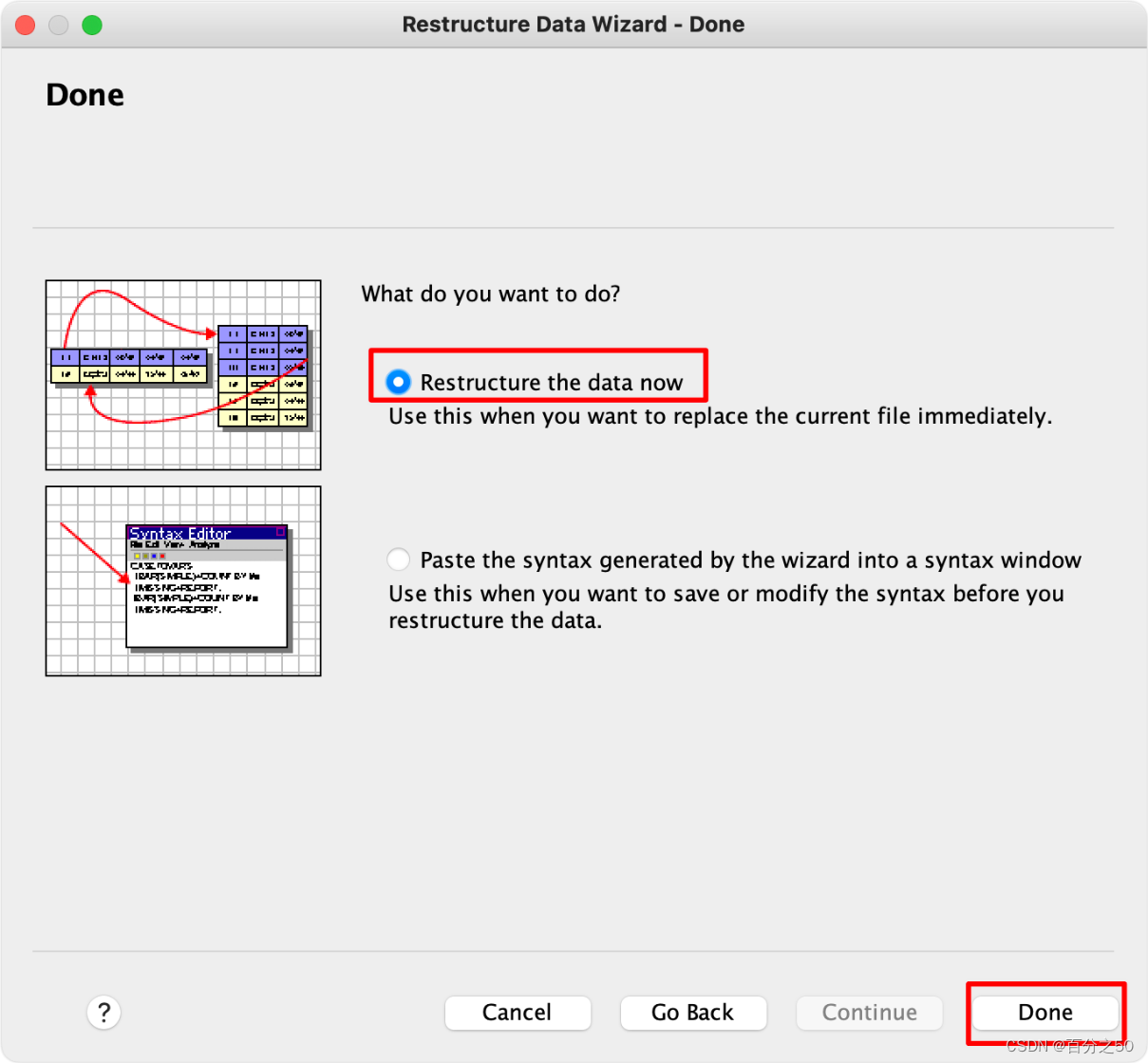
9.确定
10.可以看到新生成名为索引1的一列
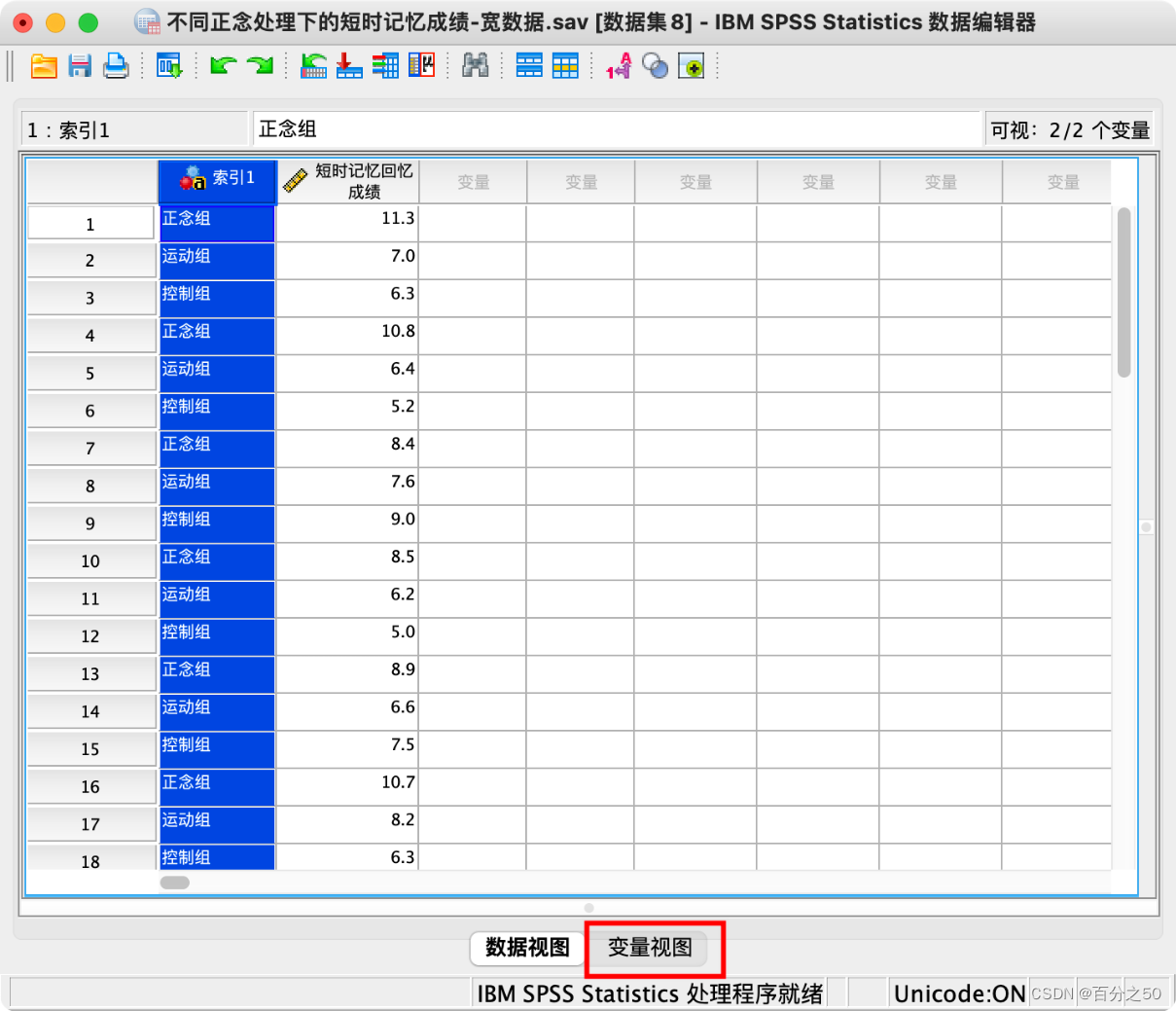
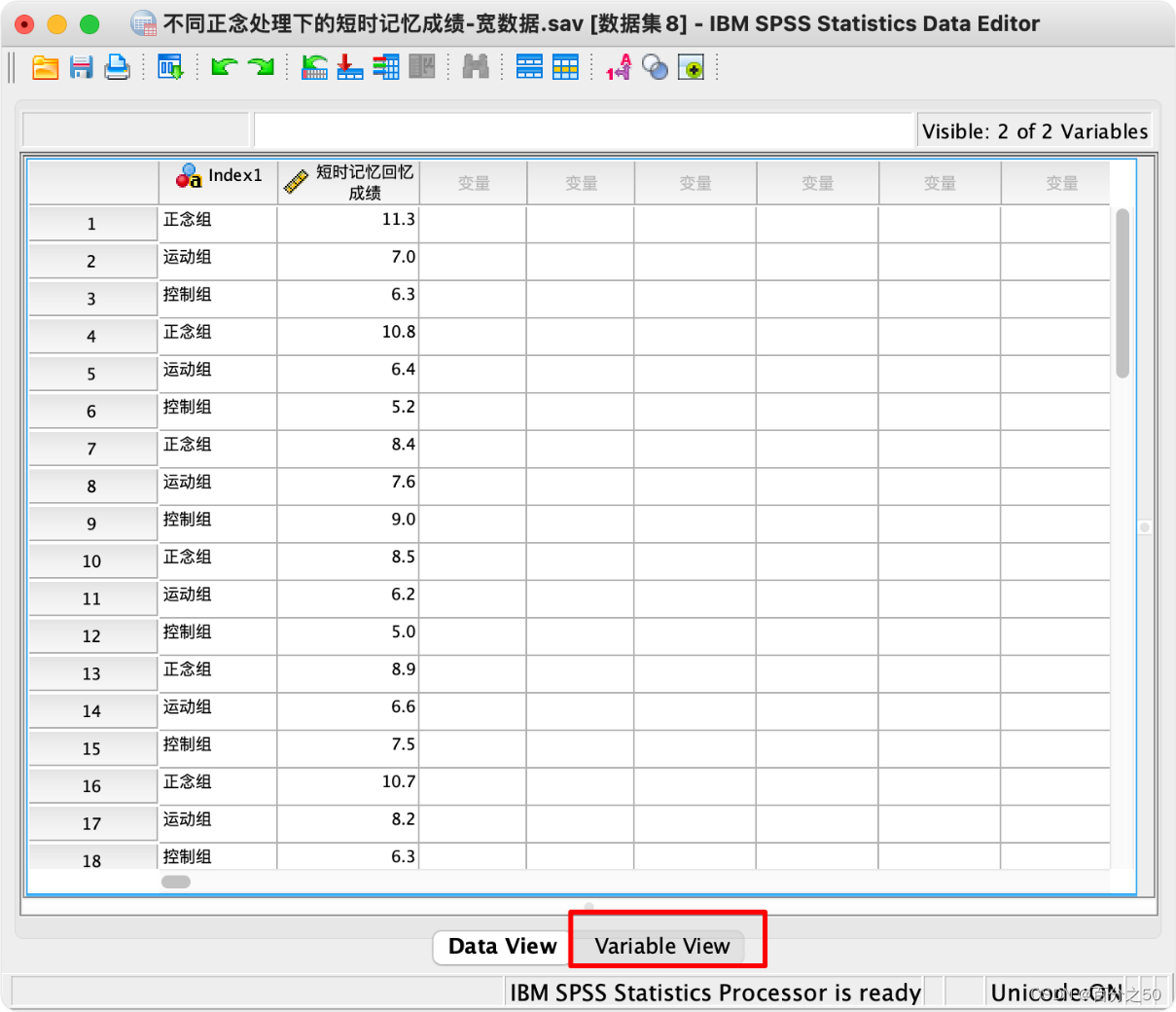
11.点一下下面的变量视图，将索引1改成组别
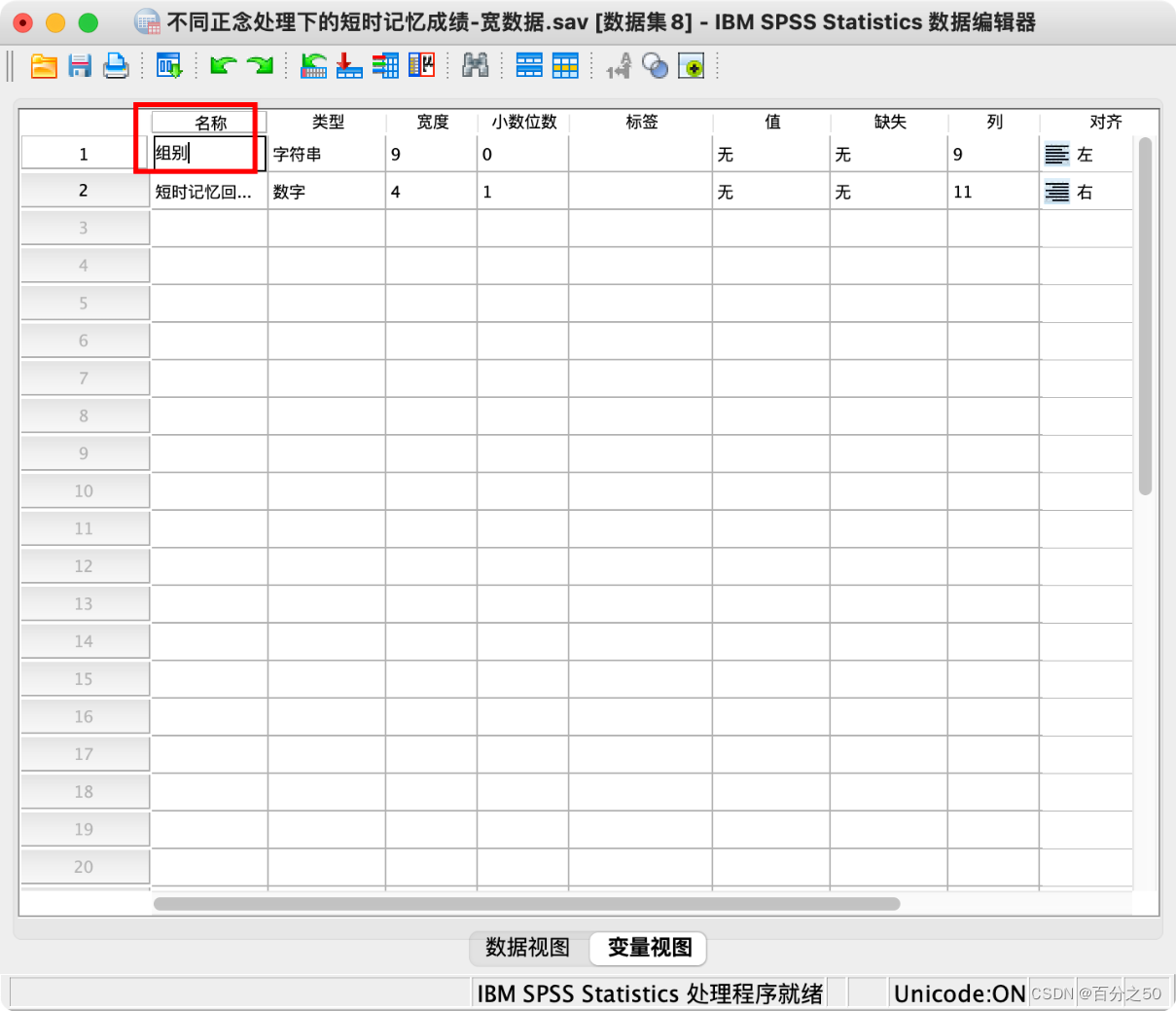
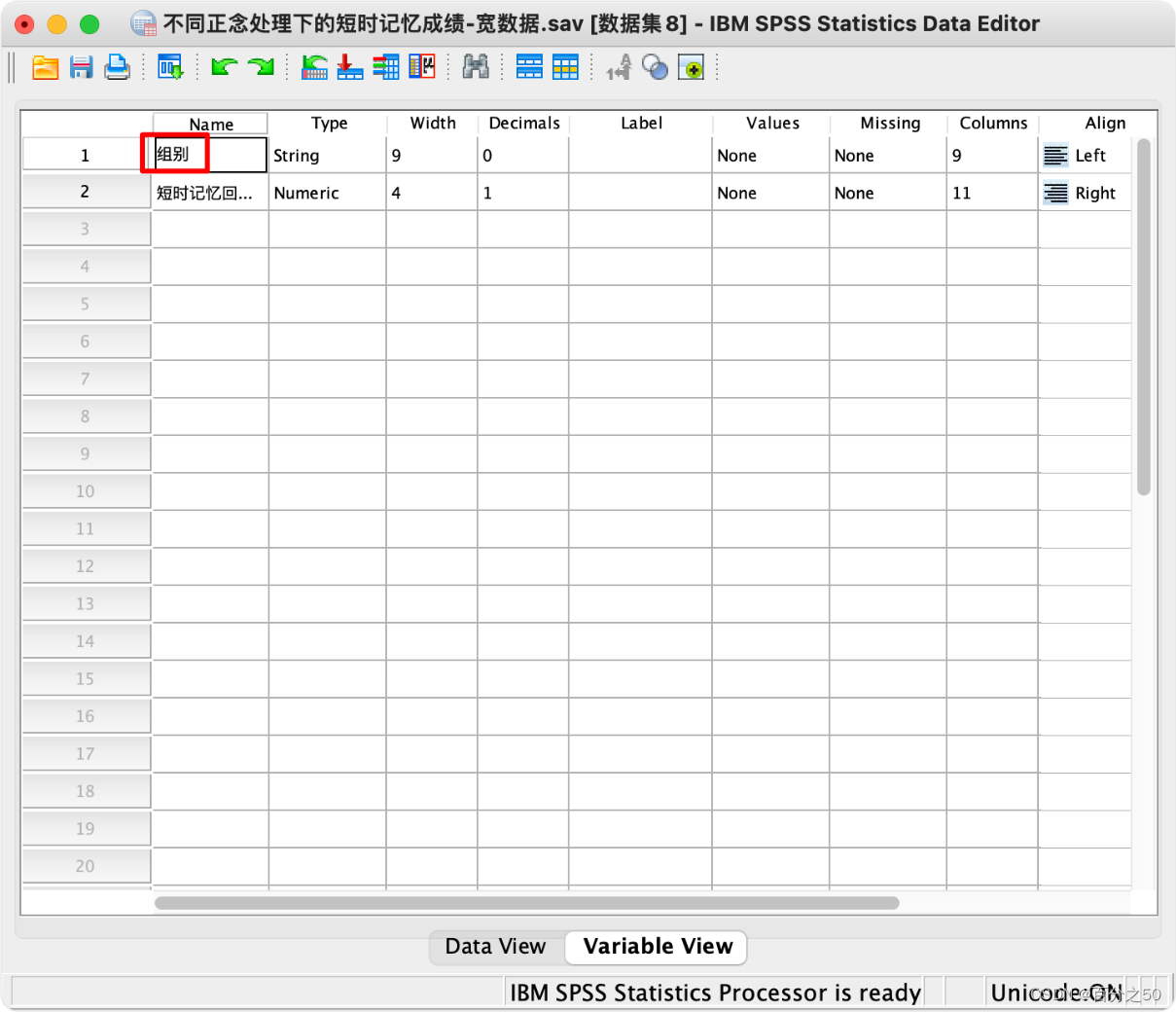
12.再将组别排序，即可获得长数据
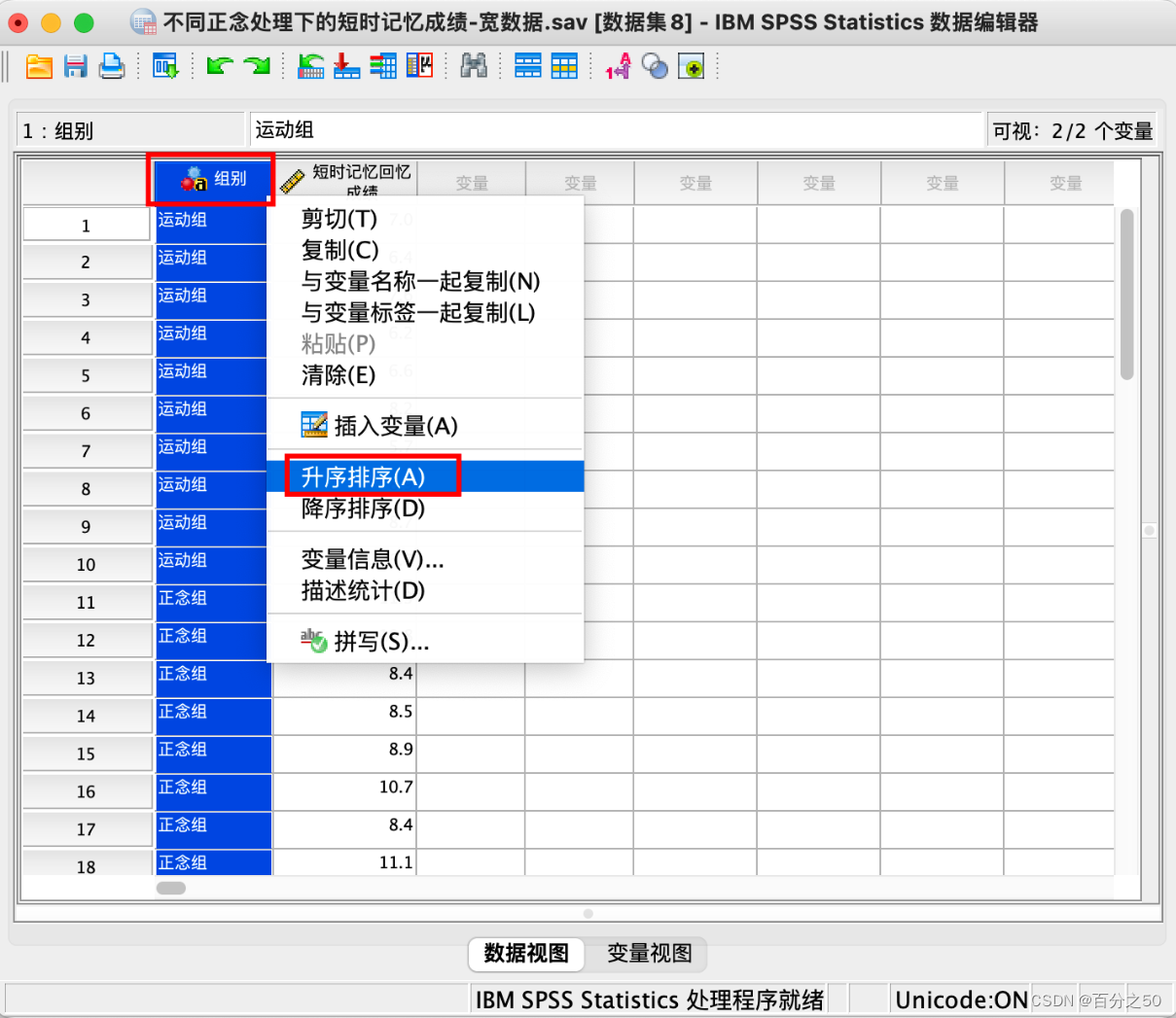
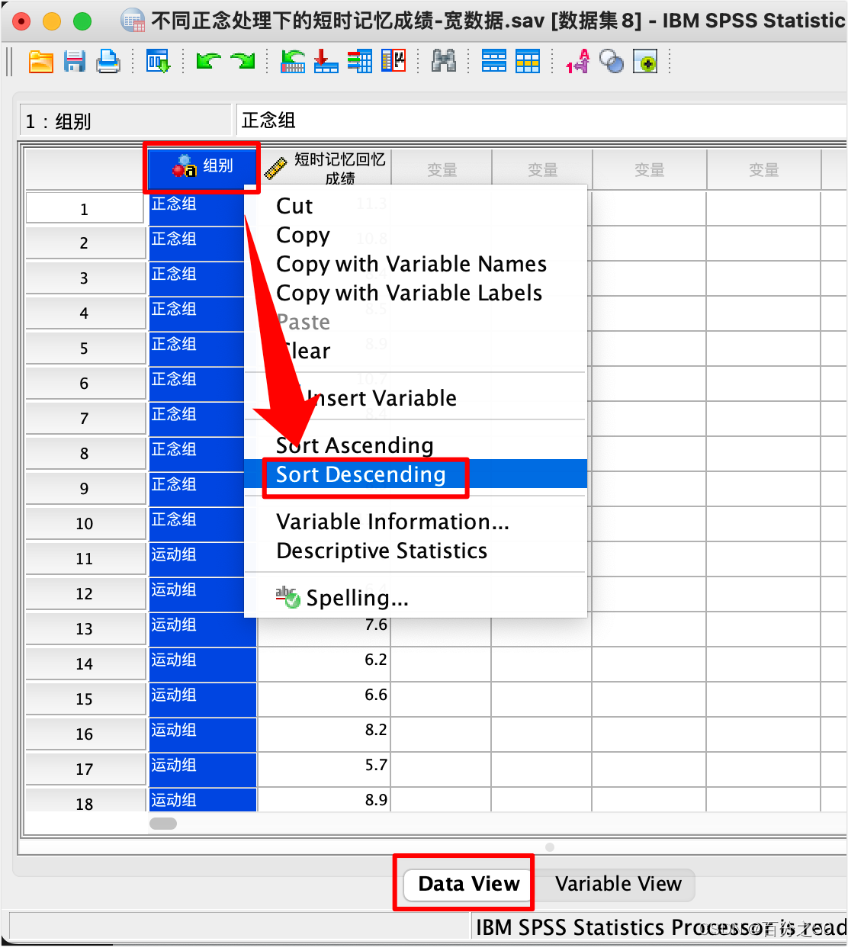
其实这样操作还不如直接在Excel里面操作，可能还方便一些，这里只是做个展示。
而且在SPSS中，如果使用“分析”-“比较平均值”下面的“单因素 ANOVA 检验…”，则不能使用字符串，如“正念组”这样，而是要转换成数字123之类的，变成组1组2组3，但是这样看起来不方便，输出结果也不好看。我们还可以使用“分析”-“一般线性模型”下的单变量，来达到方差分析的目的。
4.2 方差分析
4.2.1 Python代码
# 方差分析
def anova(melt_data):# ols（）创建一线性回归分析模型model_ols = ols('%s~C(%s)' % (dependent, independent), melt_data).fit()# anova_lm（）函数创建模型生成方差分析表anova_table = anova_lm(model_ols, typ=2)print("\n=================以下为方差分析表====================")print(anova_table)
Python输出结果：
4.2.2 SPSS操作
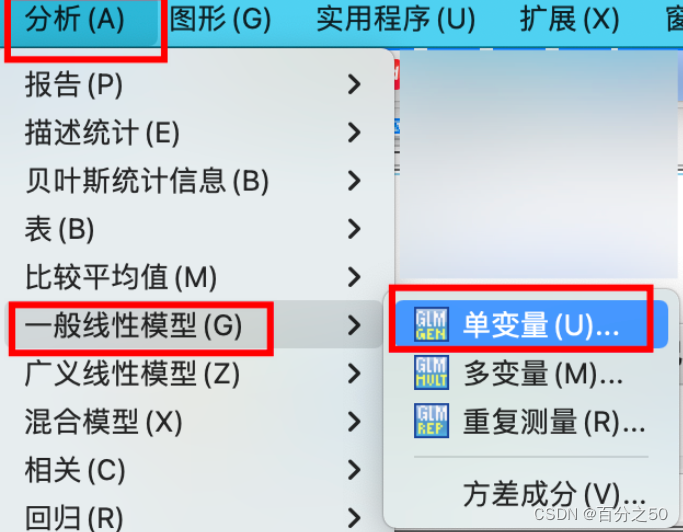
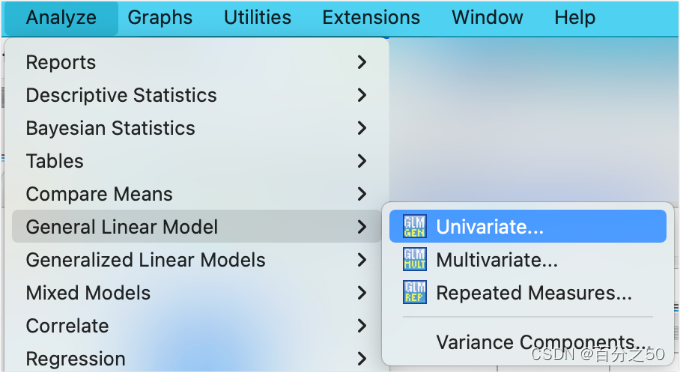
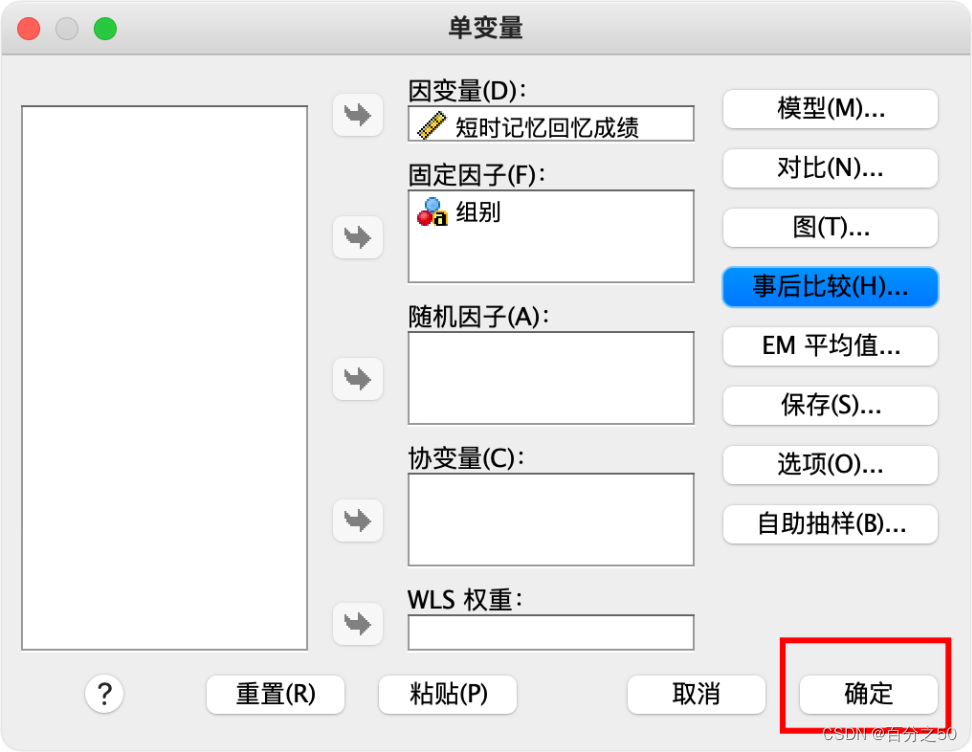
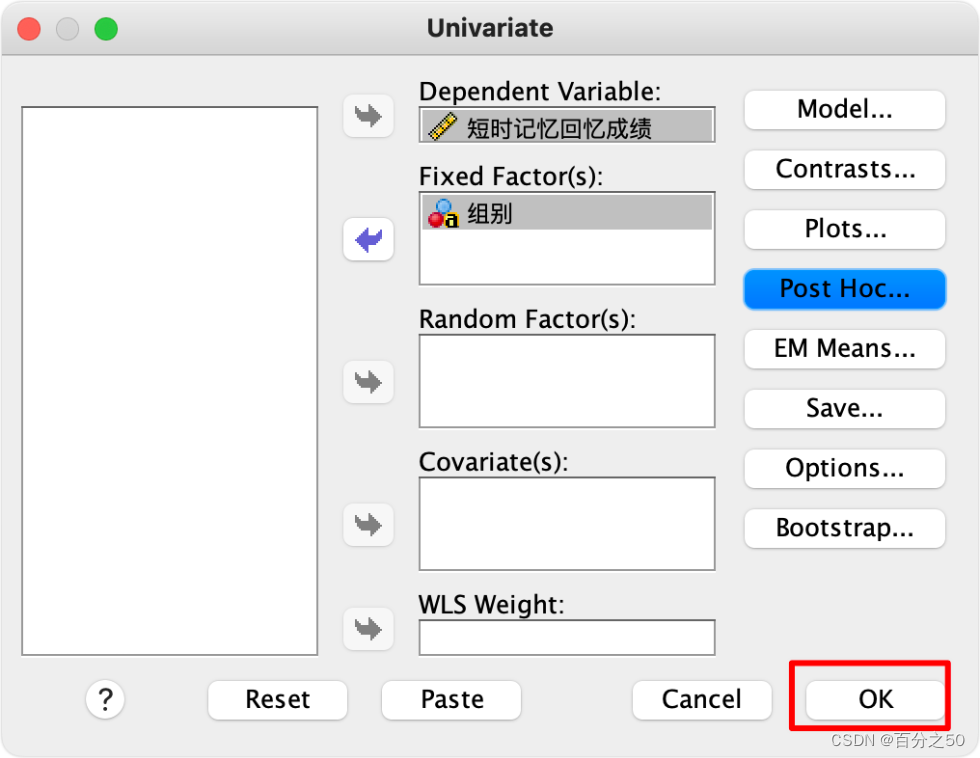
一般这里我们会按需要点击“图”、“事后比较”、“选项”这些来输出一些内容，比如描述统计、齐性检验，交互图什么的，不过这里暂时不需要，为了让输出纯粹一点，选好因变量和固定因子直接点确定即可。
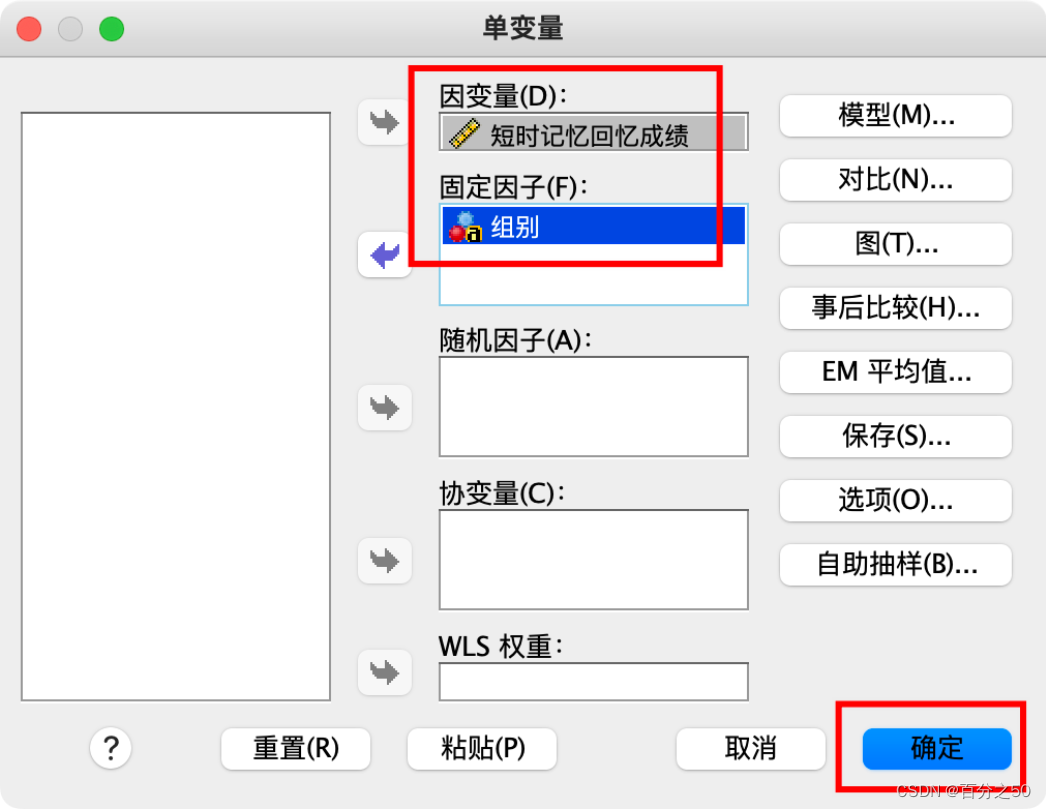
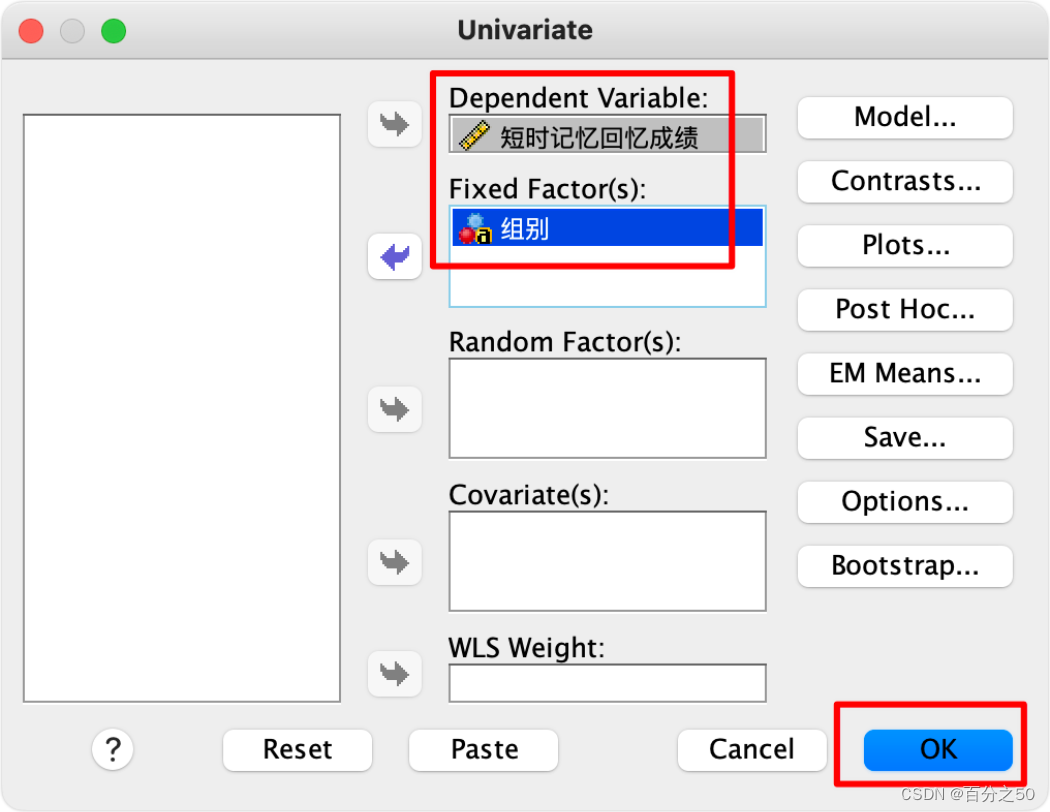
SPSS输出结果：
中文版
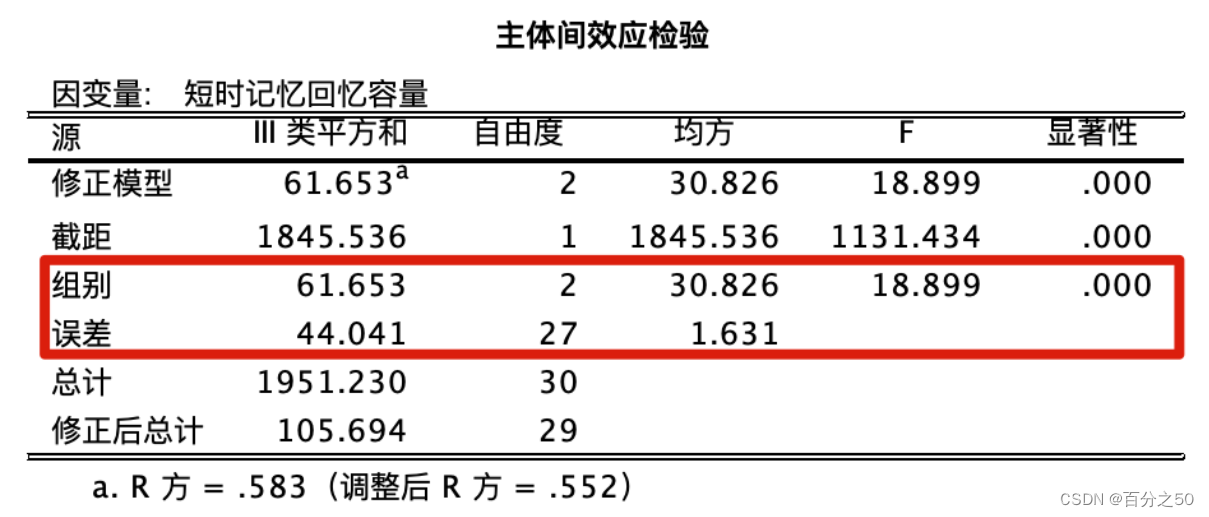
英文版
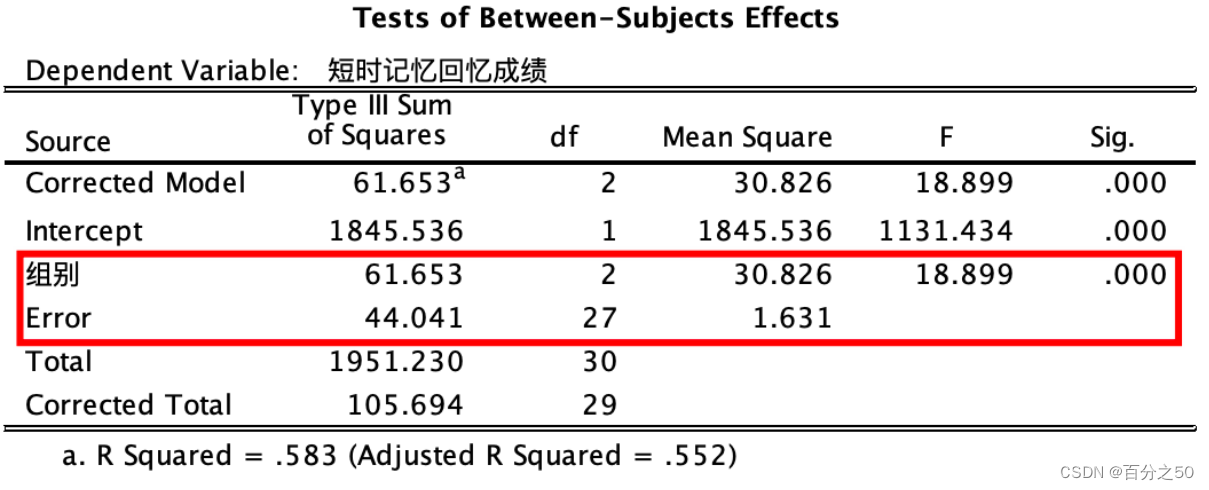
4.3 事后比较
4.3.1 Python代码
# 事后比较
def multiple_comparisons(melt_data):# 进行事后比较分析print("\n=================事后比较分析结果====================")print(pairwise_tukeyhsd(melt_data[dependent], melt_data[independent]))
Python输出结果：
4.3.2 SPSS操作
选择事后比较
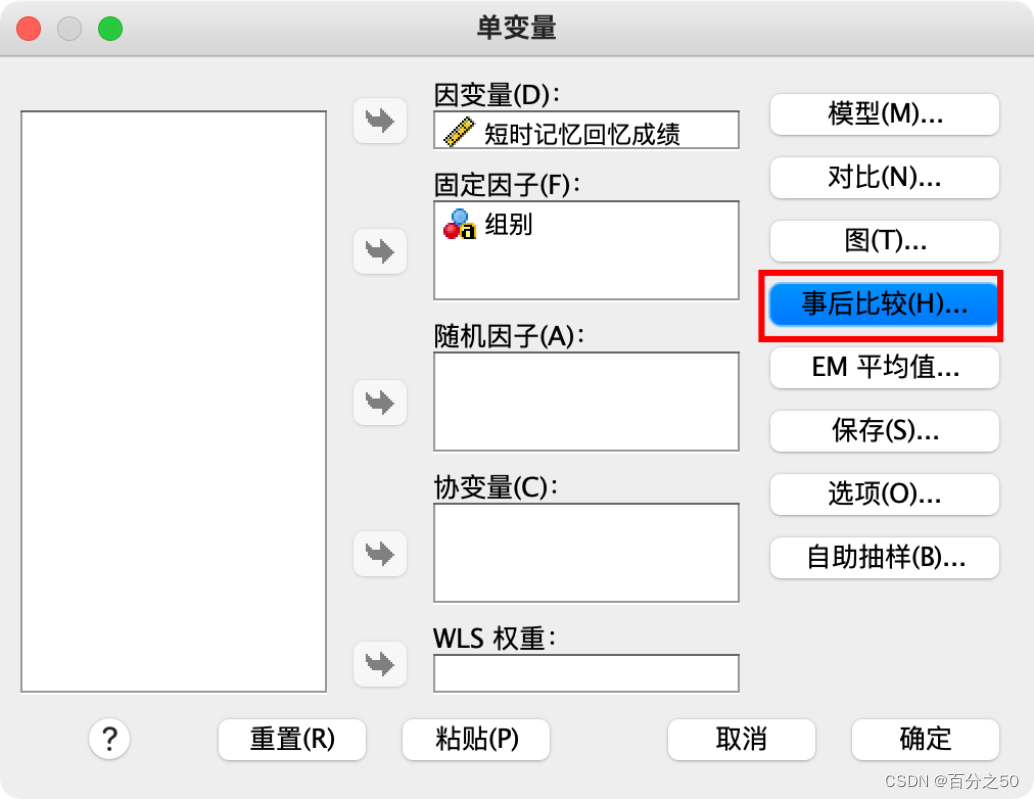
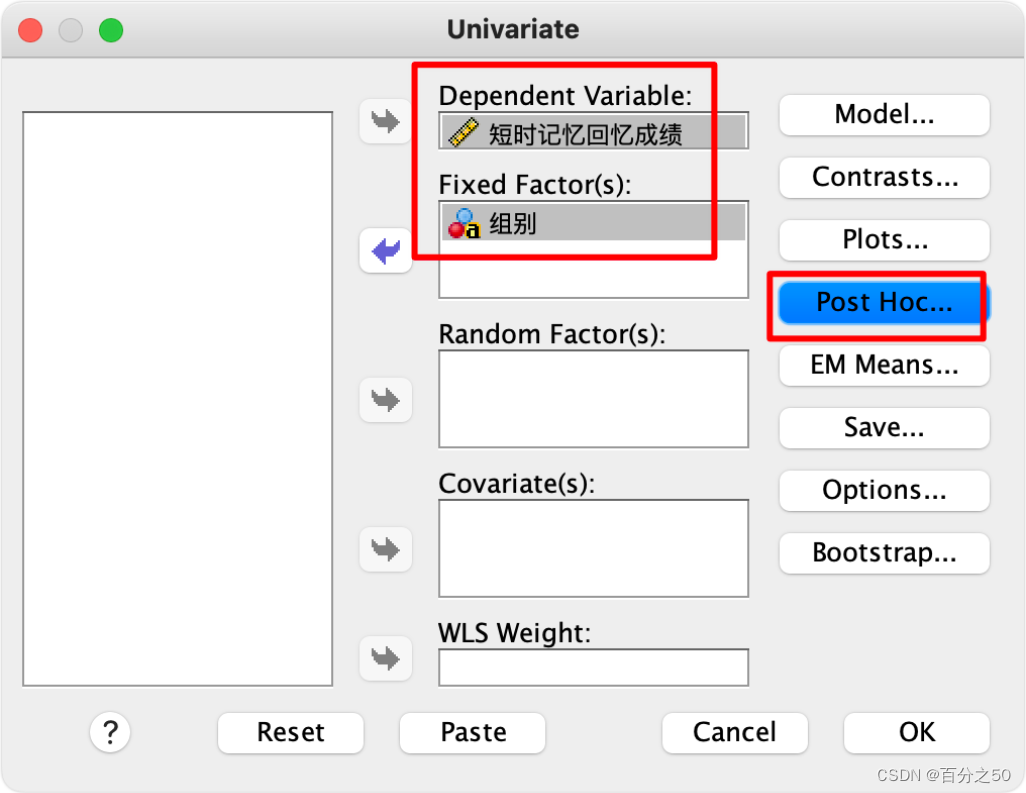
选择“图基（Tukey）”即可
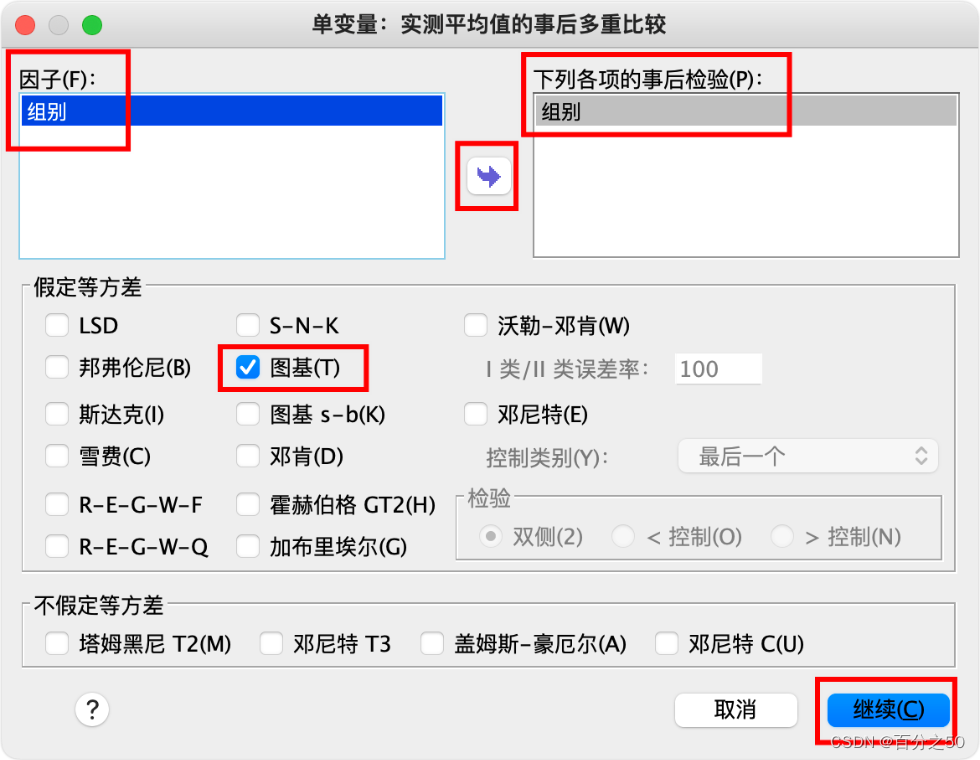
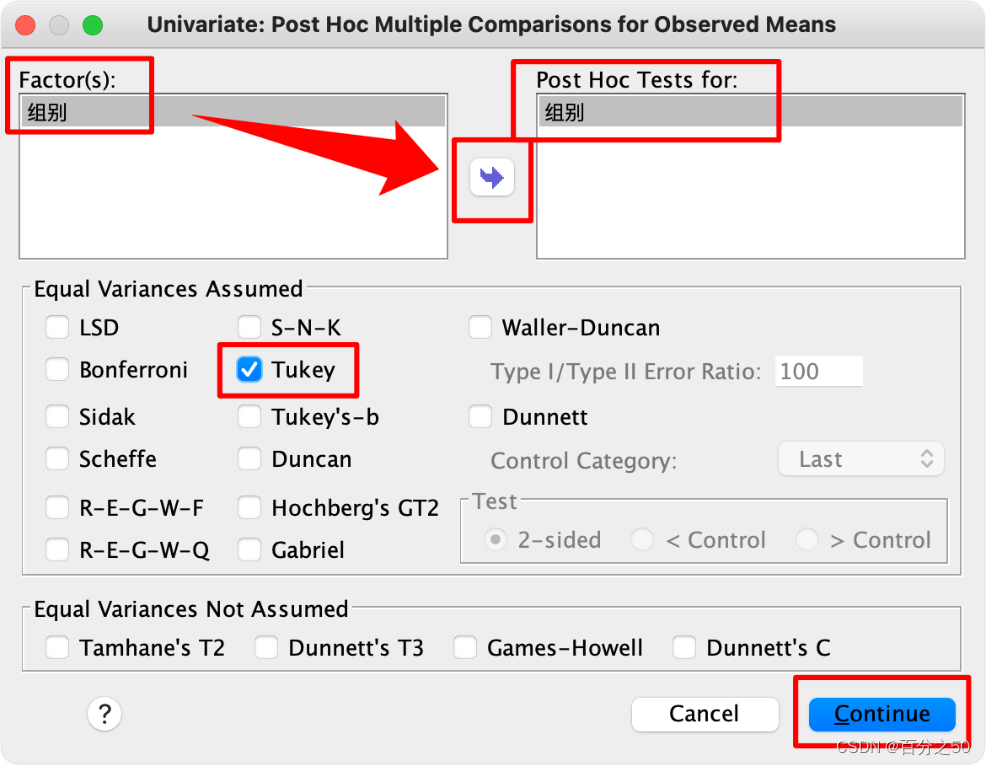
然后点确定
SPSS输出结果：
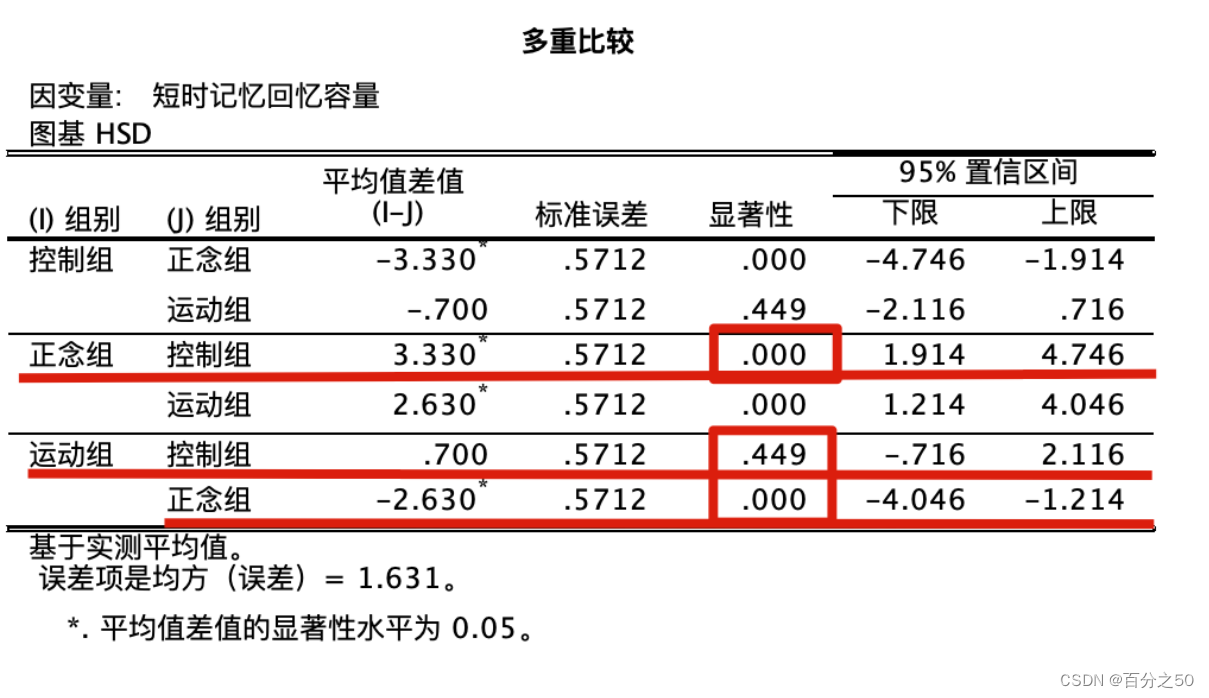
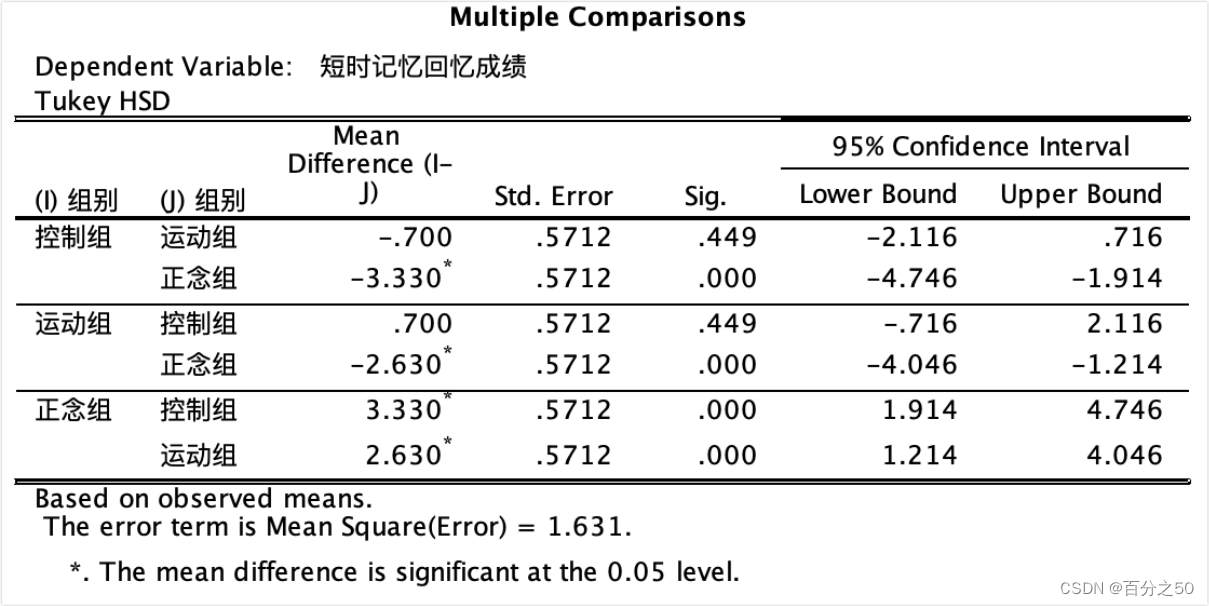
这一步同时还会输出主体间因子 Between-Subjects Factors，齐性子集 Homogeneous Subsets和前面的主体间效应检验 Tests of Between-Subjects Effects，不过这不是重点，我们主要关注和代码对应的部分即可。
4.4 箱型图
4.4.1 Python代码
# 设置画图参数
def define_plt():plt.rcParams['font.sans-serif'] = ['SimHei', ] # 设置汉字字体plt.rcParams['font.size'] = 12 # 字体大小plt.rcParams['axes.unicode_minus'] = False # 正常显示负号# 显示箱型线，检查是否有极端数值
def show_boxplot(melt_data):sns.boxplot(x=independent, y=dependent, data=melt_data)plt.show() # 需要放最后运行，否则会阻挡后面程序的运行
Python输出结果：
4.4.2 SPSS操作
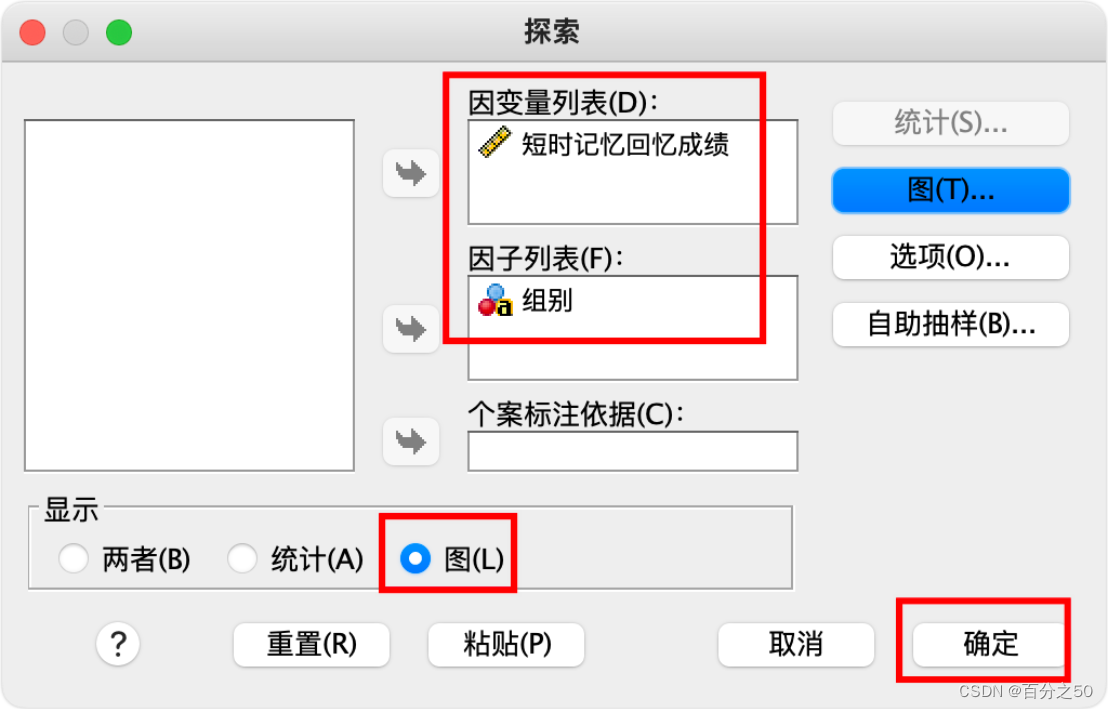
由于这里我们只是想看一下箱型图，不想输出太多内容，所以左下角点击只显示图即可，如果还想输出正态性检验，Q-Q图之类的，可以按需要点击右侧的按钮设置选取。
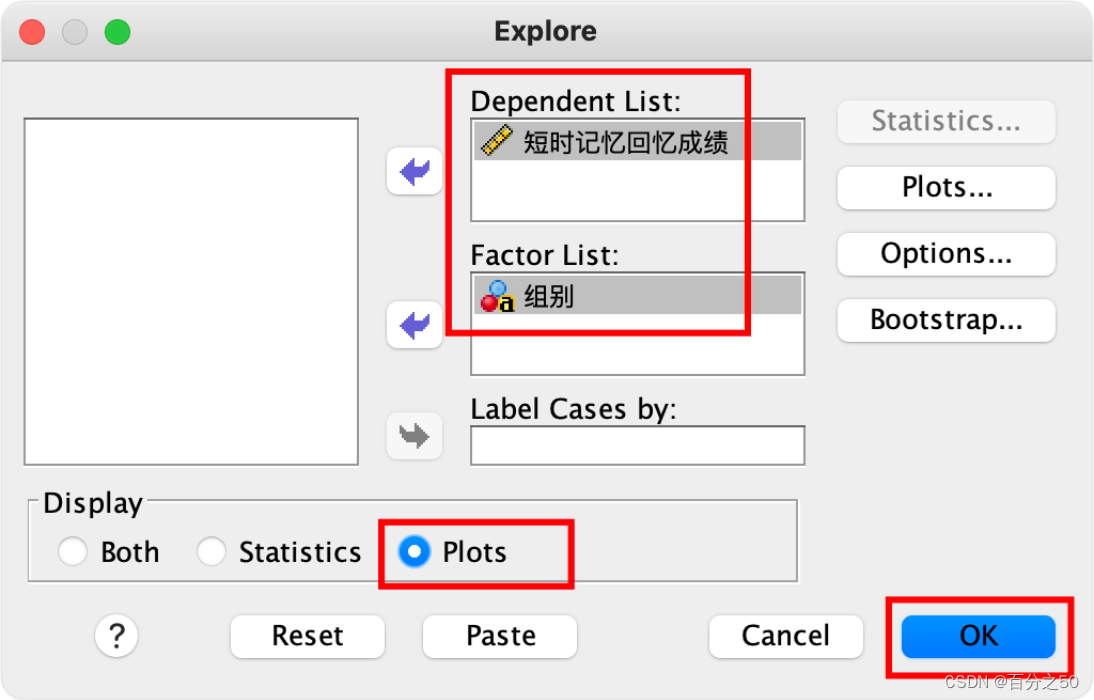
SPSS输出结果：
END
这篇关于Python实现单因素方差分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
![C#实战|大乐透选号器[6]：实现实时显示已选择的红蓝球数量](https://i-blog.csdnimg.cn/direct/cda2638386c64e8d80479ab11fcb14a9.png)
