机器学习入门（5）——正则化(Regularization)

本文主要是介绍机器学习入门（5）——正则化(Regularization)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

过拟合问题（The Problem of Overfitting）
代价函数（Cost Function）
正则化线性回归（Regularized Linear Regression）
正则化的逻辑回归模型（Regularized Logistic Regression）

过拟合问题（The Problem of Overfitting）

回归问题的例子：
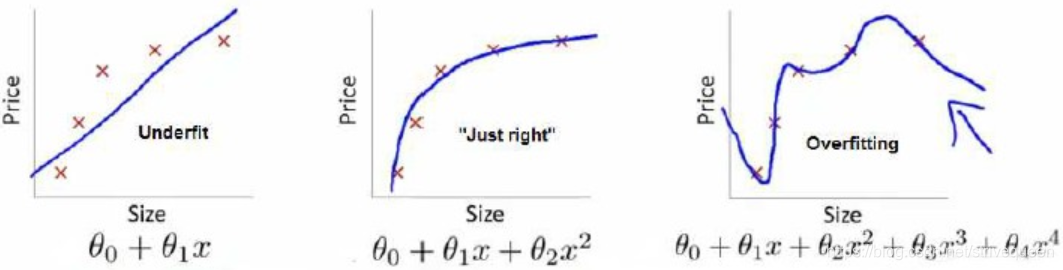
在这里插入图片描述
第一个模型是一个线性模型，欠拟合，不能很好地适应我们的训练集；第三个模型是一个四次方的模型，过于强调拟合原始数据，而丢失了算法的本质：预测新数据。我们可以看出，若给出一个新的值使之预测，它将表现的很差，是过拟合，虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好；而中间的模型似乎最合适。
分类问题的例子：
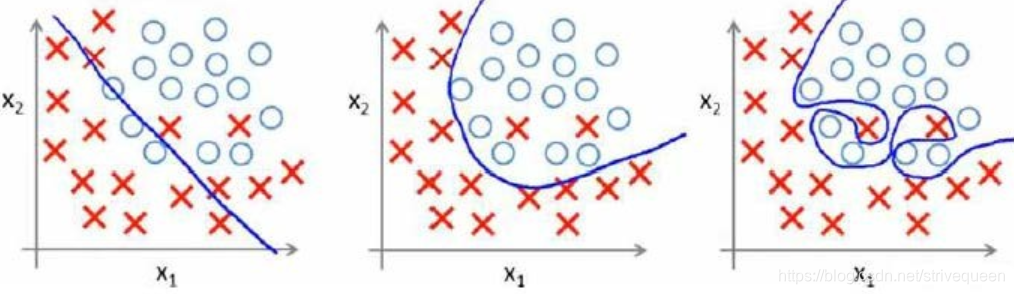
在这里插入图片描述
以多项式理解， x的次数越高，拟合的越好，但相应的预测的能力就可能变差。
过拟合问题处理方法：

丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如PCA）
正则化。保留所有的特征，但是减少参数的大小（magnitude）。

代价函数（Cost Function）

假如我们有非常多的特征，我们并不知道其中哪些特征我们要惩罚，我们将对所有的特征进行惩罚，并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设：
$J(\theta)=\frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$
其中 $\lambda$ 又称为正则化参数（Regularization Parameter）。注：根据惯例，我们不对 $\theta_{0}$ 进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示：

在这里插入图片描述

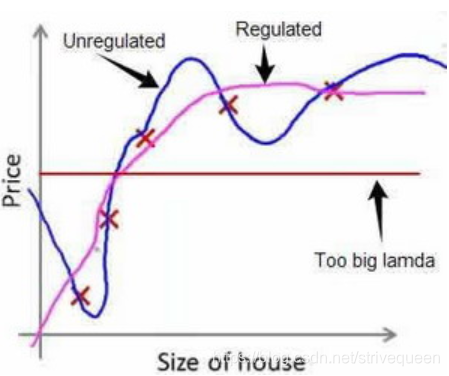
正则化线性回归（Regularized Linear Regression）

Repeat until convergence{
${\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}})$
${\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}]$
$f o r$ $j = 1, 2, . . . n$
}
如果我们要使用梯度下降法令代价函数最小化，因为我们未对 ${\theta_0}$ 进行正则化，所以梯度下降算法将分两种情形：
在这里插入图片描述

正则化的逻辑回归模型（Regularized Logistic Regression）

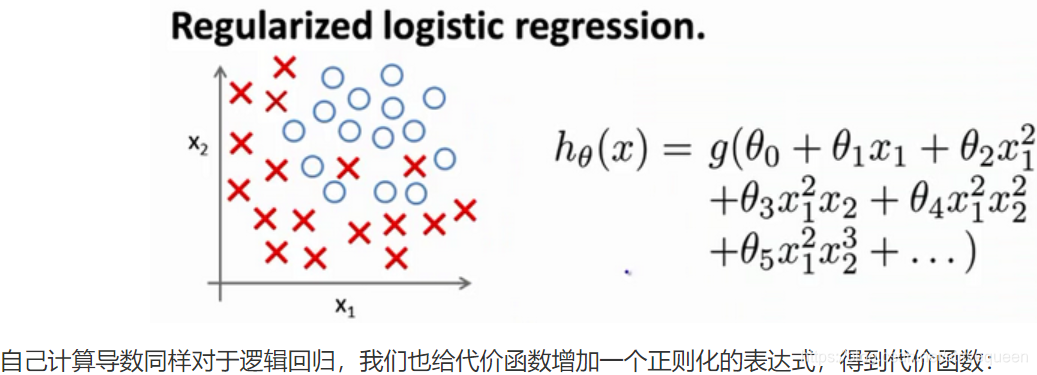
在这里插入图片描述
$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$
Python代码：

import numpy as np

def costReg(theta, X, y, learningRate):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)first = np.multiply(-y, np.log(sigmoid(X*theta.T)))second = np.multiply((1 - y), np.log(1 - sigmoid(X*theta.T)))reg = (learningRate / (2 * len(X))* np.sum(np.power(theta[:,1:theta.shape[1]],2))return np.sum(first - second) / (len(X)) + reg

要最小化该代价函数，通过求导，得出梯度下降算法为：
Repeat until convergence{
${\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}})$
${\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}]$
$f o r$ $j = 1, 2, . . . n$
}
注：看上去同线性回归一样，但是知道 $h_{\theta}(x)=g\left(\theta^{T} X\right)$ ，所以与线性回归不同。