生物地理学算法

本文主要是介绍生物地理学算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

生物地理学优化算法

生物地理学优化算法（biogeography-based optimization,BBO）源于生物地理学理论，通过模仿栖息地之间物种迁移和变异对优化问题进行求解，由Simon于2008年提出。

BBO算法由一群可行解组成，这些可行解被称为栖息地（Habitat），每个可行解的特征称为适宜性指数变量（Suitability index variables，SIVs），可行解的优劣使用栖息地适宜性指数（Habitat suitability index，HSI）进行量化，类似于其他基于种群的优化算法中的 “适应度”，HSI的高低表示可行解的优劣。在算法寻优过程中高HSI可行解倾向于与低HSI可行解共享其特征，因此，较差的可行解会从较好的可行解中接受大量新特征。生物地理学算法与优化问题的对应关系如下表所示。

BBO	优化问题
栖息地	可行解：$x_i=(x_{i1},x_{i2},\dots ,x_{iD})$
适宜指数变量	自变量：$x_{ij}$
栖息适宜指数	适应度

迁移和突变是BBO算法的两个重要操作，栖息地之间通过迁移和突变操作，增强物种间信息的交换与共享，提高物种的多样性。

迁移

栖息地物种的数量$s$影响迁入率$\lambda$和迁出率$\mu$，迁入率$\lambda$是$s$的单调非递增函数,迁出率$\mu$是$s$的单调非递减函数。

• immigration：迁入
  $$\lambda (s)=I\cdot (1-\frac{s}{S_{max}})\text{\hspace{1em}(1)}$$
• emigration：迁出
  $$\mu (s)=\frac{E\cdot s}{S_{max}}\text{\hspace{1em}(2)}$$
  其中，$S_{max}$表示栖息地容纳生物种类最大数量，$I$和$E$分别表示最大迁入率和最大迁出率，通常考虑$I=E$，栖息地物种数量与栖息地适宜性指数成正比。

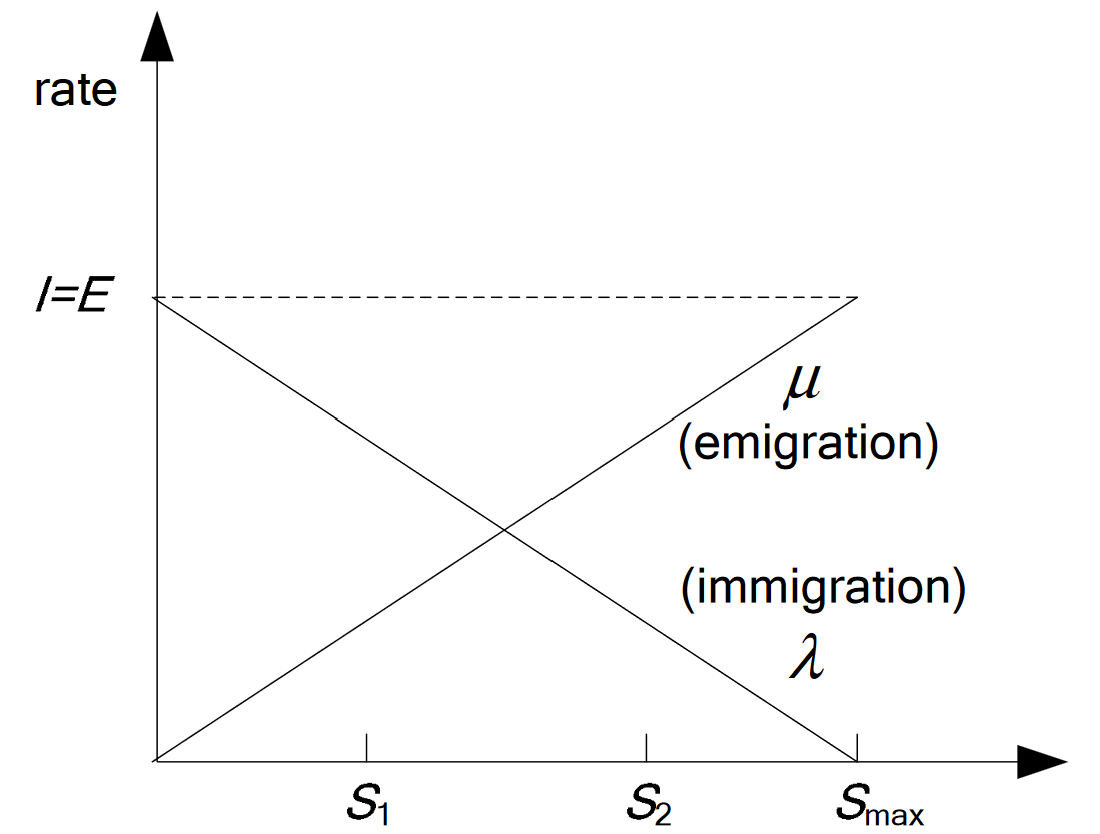
在一定的概率下，根据其他解对当前解进行调整，调整逻辑如下：

1. 对于当前解$x_i$根据迁入概率$\lambda$决定是否对$x_i$中的决策变量$x_{ij}$进行调整；
2. 对于需要调整的$x_{ij}$，根据迁出概率$\mu$决定选择哪一个$x_{kj}$替代$x_{ij}$。对于每一个$x_{ij}$都需要根据特定规则（如轮盘赌）进行选择$x_{kj}$。

突变

灾难性事件（来自邻近栖息地的异常大的漂浮物、疾病、自然灾害等）会彻底改变自然栖息地的 HSI。因此，栖息地的HSI可能会因随机事件而突然发生变化，BBO将此类事件建模为突变。

$$m(s)=m_{max}\cdot (1-\frac{P_s}{P_{max}})\text{\hspace{1em}(3)}$$

其中，$P_s$表示物种数量为$s$的概率，$m_{max}$为最大变异概率， P m a x = m a x { P s } P_{max}=max\{P_s\} Pmax​=max{Ps​}。

初始化

初始解应当覆盖整个搜索空间，一般采用均匀分布随机生成初始解。
$$x_{ij}^0=x_{i,j}^{min}+rand(0,1)\cdot (x_{i,j}^{max}-x_{i,j}^{min})\text{\hspace{1em}(4)}$$
其中，rand(0,1)表示0-1之间的随机数，$x_{ij}^{max}$和$x_{ij}^{min}$分别表示该问题第j个维度变量的上下界。

算法超参数

• I:最大迁入率
• E:最大迁出率
• $m_{max}$:最大变异率
• NP:种群大小
• G:最大迭代数

伪代码

———————————————————————————————
输入:超参数$(I,E,m_{max},NP,Gmax)$和搜索边界$X_{min}$，$X_{max}$
输出:最优解
1:初始化
2:根据式(4)初始化位置种群X和速度种群V
3:记录最优解
4:优化搜索
5:For G = 1:Gmax
6: \qquad For i = 1:NP
7: \qquad \qquad 根据Migration执行迁移操作
8: \qquad \qquad 根据Mutation执行变异操作
9: \qquad End
10: \qquad 更新最优解
11:End
————————————————————————————————
注：优化算法并不保证能够得到问题的最优解，因此，算法输出的最优解并非问题的整体最优解，而是搜索过程中最好的一个解。

实验

实验选取二维的平方和函数，函数的最小值在点(a,b)取得，最小值为0。
$$f(x_1,x_2)=(x_1-a{)}^2+(x_2-b{)}^2\text{\hspace{1em}(5)}$$
实验参数如下：

参数	值
问题维度D	2
种群数NP	30
最大进化次数Gmax	50
I	1
E	1
$m_{max}$	0.01
取值范围	(-100,100)

重复实验30次,结果如下表所示，算法效果差强人意。

最优值	最差值	平均值	标准差
1.652	318.571	56.772	67.403

代码获取

关注微信公众号数学模型与算法回复 生物地理学算法获取python代码

参考文献

[1] Simon, Dan . “Biogeography-Based Optimization.” IEEE Transactions on Evolutionary Computation 12.6(2009):702-713.
[2] Ma, H. , and D. Simon . “Evolutionary Computation with Biogeography-based Optimization.” Genetic Programming (2017).

这篇关于生物地理学算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---