本文主要是介绍数组题目:可以攻击国王的皇后,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:可以攻击国王的皇后
出处:1222. 可以攻击国王的皇后
难度
3 级
题目描述
要求
在一个 8 × 8 \texttt{8} \times \texttt{8} 8×8 的棋盘上,放置着若干「黑皇后」和一个「白国王」。
「黑皇后」在棋盘上的位置分布用整数坐标数组 queens \texttt{queens} queens 表示,「白国王」的坐标用数组 king \texttt{king} king 表示。
「黑皇后」的行棋规定是:横、直、斜都可以走,步数不受限制,但是,不能越子行棋。
请你返回可以直接攻击到「白国王」的所有「黑皇后」的坐标(任意顺序)。
示例
示例 1:
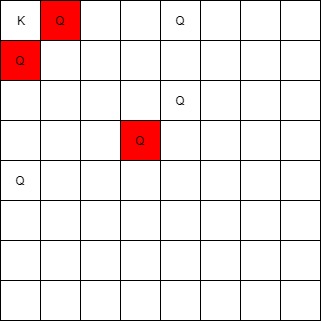
输入: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] \texttt{queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]} queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出: [[0,1],[1,0],[3,3]] \texttt{[[0,1],[1,0],[3,3]]} [[0,1],[1,0],[3,3]]
解释:
[0,1] \texttt{[0,1]} [0,1] 的皇后可以攻击到国王,因为他们在同一行上。
[1,0] \texttt{[1,0]} [1,0] 的皇后可以攻击到国王,因为他们在同一列上。
[3,3] \texttt{[3,3]} [3,3] 的皇后可以攻击到国王,因为他们在同一条对角线上。
[0,4] \texttt{[0,4]} [0,4] 的皇后无法攻击到国王,因为她被位于 [0,1] \texttt{[0,1]} [0,1] 的皇后挡住了。
[4,0] \texttt{[4,0]} [4,0] 的皇后无法攻击到国王,因为她被位于 [1,0] \texttt{[1,0]} [1,0] 的皇后挡住了。
[2,4] \texttt{[2,4]} [2,4] 的皇后无法攻击到国王,因为她和国王不在同一行/列/对角线上。
示例 2:
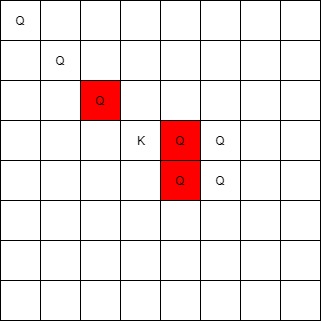
输入: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] \texttt{queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]} queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出: [[2,2],[3,4],[4,4]] \texttt{[[2,2],[3,4],[4,4]]} [[2,2],[3,4],[4,4]]
示例 3:

输入: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4] \texttt{queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]} queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]] \texttt{[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]} [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]
数据范围
- 1 ≤ queens.length ≤ 63 \texttt{1} \le \texttt{queens.length} \le \texttt{63} 1≤queens.length≤63
- queens[i].length = 2 \texttt{queens[i].length}=\texttt{2} queens[i].length=2
- 0 ≤ queens[i][j] < 8 \texttt{0} \le \texttt{queens[i][j]}<\texttt{8} 0≤queens[i][j]<8
- king.length = 2 \texttt{king.length}=\texttt{2} king.length=2
- 0 ≤ king[0], king[1] < 8 \texttt{0} \le \texttt{king[0], king[1]}<\texttt{8} 0≤king[0], king[1]<8
- 一个棋盘格上最多只能放置一枚棋子
解法
思路和算法
最朴素的想法是检查每个「黑皇后」是否可以攻击到「白国王」,需要遍历每个「黑皇后」,对每个「黑皇后」需要检查 8 8 8 个方向分别是否可以攻击到「白国王」。该做法的时间复杂度较高。
可以换一个思路,一个「黑皇后」可以攻击到「白国王」,当且仅当两者位于同一条横线、直线或斜线上,且两者之间没有其他棋子。由于最多有 8 8 8 个方向可以攻击「白国王」,因此可以攻击到「白国王」的「黑皇后」最多有 8 8 8 个。从「白国王」出发,分别向 8 8 8 个方向遍历,每个方向上的第一个「黑皇后」就是可以攻击到「白国王」的「黑皇后」。
为了判断是否遇到「黑皇后」,需要存储每个「黑皇后」的位置。可以创建一个 8 8 8 行 8 8 8 列的二维数组,其中的每个元素表示该位置是否有「黑皇后」。从「白国王」所在的行和列出发,分别向 8 8 8 个方向遍历,遍历过程中记录当前遍历到的行下标和列下标,即可通过行下标和列下标知道该位置是否有「黑皇后」。
当一个方向上遇到「黑皇后」之后即停止在该方向上继续寻找,因为之后的「黑皇后」会被当前的「黑皇后」挡住而不能攻击到「白国王」。
代码
class Solution {public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {final int SIDE = 8;boolean[][] chessboard = new boolean[SIDE][SIDE];for (int[] queen : queens) {chessboard[queen[0]][queen[1]] = true;}int[][] directions = {{-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1}};List<List<Integer>> queensAttackList = new ArrayList<List<Integer>>();for (int[] direction : directions) {int row = king[0] + direction[0], column = king[1] + direction[1];while (row >= 0 && row < SIDE && column >= 0 && column < SIDE) {if (chessboard[row][column]) {List<Integer> curQueen = new ArrayList<Integer>(Arrays.asList(row, column));queensAttackList.add(curQueen);break;} else {row += direction[0];column += direction[1];}}}return queensAttackList;}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是棋盘的边长,这道题中 n = 8 n=8 n=8。
首先需要遍历每个「黑皇后」的位置,并在二维数组中记录,「黑皇后」最多有 n 2 − 1 n^2-1 n2−1 个,因此时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
然后需要在「白国王」的 8 8 8 个方向上寻找「黑皇后」, 8 8 8 个方向包括 4 4 4 条直线,每条直线上需要遍历的位置数都少于 n n n,因此需要遍历的总位置数少于 4 n 4n 4n,时间复杂度是 O ( n ) O(n) O(n)。
总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。 -
空间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是棋盘的边长,这道题中 n = 8 n=8 n=8。需要创建一个 n n n 行 n n n 列的二维数组存储每个元素是否是「黑皇后」。
这篇关于数组题目:可以攻击国王的皇后的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



