本文主要是介绍数组题目:可以被一步捕获的棋子数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:可以被一步捕获的棋子数
出处:999. 可以被一步捕获的棋子数
难度
2 级
题目描述
要求
在一个 8 × 8 \texttt{8} \times \texttt{8} 8×8 的棋盘上,有一个白色的车( Rook \texttt{Rook} Rook),用字符 ‘R’ \texttt{`R'} ‘R’ 表示。棋盘上还可能存在空方块,白色的象( Bishop \texttt{Bishop} Bishop)以及黑色的卒( pawn \texttt{pawn} pawn),分别用字符 ‘.’ \texttt{`.'} ‘.’, ‘B’ \texttt{`B'} ‘B’ 和 ‘p’ \texttt{`p'} ‘p’ 表示。不难看出,大写字符表示的是白棋,小写字符表示的是黑棋。
车按国际象棋中的规则移动。东,西,南,北四个基本方向任选其一,然后一直向选定的方向移动,直到满足下列四个条件之一:
- 棋手选择主动停下来。
- 棋子因到达棋盘的边缘而停下。
- 棋子移动到某一方格来捕获位于该方格上敌方(黑色)的卒,停在该方格内。
- 车不能进入/越过已经放有其他友方棋子(白色的象)的方格,停在友方棋子前。
你现在可以控制车移动一次,请你统计有多少敌方的卒处于你的捕获范围内(即,可以被一步捕获的棋子数)。
示例
示例 1:

输入: [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]] \texttt{[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]} [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","R",".",".",".","p"],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出: 3 \texttt{3} 3
解释:
在本例中,车能够捕获所有的卒。
示例 2:

输入: [[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]] \texttt{[[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]} [[".",".",".",".",".",".",".","."],[".","p","p","p","p","p",".","."],[".","p","p","B","p","p",".","."],[".","p","B","R","B","p",".","."],[".","p","p","B","p","p",".","."],[".","p","p","p","p","p",".","."],[".",".",".",".",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出: 0 \texttt{0} 0
解释:
象阻止了车捕获任何卒。
示例 3:
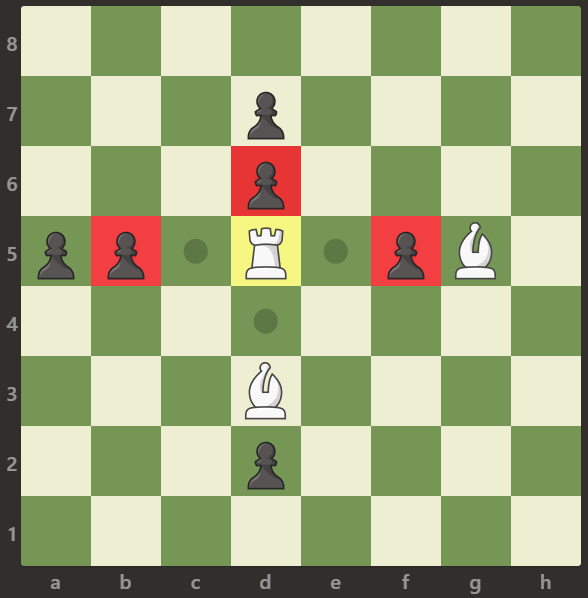
输入: [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]] \texttt{[[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]]} [[".",".",".",".",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".","p",".",".",".","."],["p","p",".","R",".","p","B","."],[".",".",".",".",".",".",".","."],[".",".",".","B",".",".",".","."],[".",".",".","p",".",".",".","."],[".",".",".",".",".",".",".","."]]
输出: 3 \texttt{3} 3
解释:
车可以捕获位置 b5 \texttt{b5} b5, d6 \texttt{d6} d6 和 f5 \texttt{f5} f5 的卒。
数据范围
- board.length = board[i].length = 8 \texttt{board.length}=\texttt{board[i].length}=\texttt{8} board.length=board[i].length=8
- board[i][j] \texttt{board[i][j]} board[i][j] 可以是 ‘R’ \texttt{`R'} ‘R’, ‘.’ \texttt{`.'} ‘.’, ‘B’ \texttt{`B'} ‘B’ 或 ‘p’ \texttt{`p'} ‘p’
- 只有一个格子上存在 board[i][j] = ‘R’ \texttt{board[i][j]}=\texttt{`R'} board[i][j]=‘R’
解法
思路和算法
首先需要找到白色的车在棋盘上的位置,即所在的行和列。
然后需要判断白色的车分别往四个方向移动时,是否可以捕获黑色的卒。由于只能移动一次,因此每个方向最多可以捕获一个黑色的卒,可以捕获的黑色的卒的总数不会超过 4 4 4 个。对于每个方向,如果遇到了黑色的卒,则将其捕获,然后停止移动,如果遇到了白色的象或棋盘边缘,则停止移动。
代码
class Solution {public int numRookCaptures(char[][] board) {int rookRow = -1, rookColumn = -1;int rows = board.length, columns = board[0].length;int totalSquares = rows * columns;for (int i = 0; i < totalSquares; i++) {int row = i / columns, column = i % columns;if (board[row][column] == 'R') {rookRow = row;rookColumn = column;break;}}int count = 0;int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};for (int[] direction : directions) {int tempRow = rookRow + direction[0], tempColumn = rookColumn + direction[1];while (tempRow >= 0 && tempRow < rows && tempColumn >= 0 && tempColumn < columns) {if (board[tempRow][tempColumn] != '.') {if (board[tempRow][tempColumn] == 'p') {count++;}break;}tempRow += direction[0];tempColumn += direction[1];}}return count;}
}
复杂度分析
-
时间复杂度: O ( n 2 ) O(n^2) O(n2),其中 n n n 是棋盘的边长,这道题中 n = 8 n=8 n=8。
寻找白色的车需要遍历棋盘,时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
在四个方向判断有多少敌方的卒可以被一步捕获,最多需要遍历除了车所在的格子之外的 2 n − 2 2n-2 2n−2 个格子,时间复杂度是 O ( n ) O(n) O(n)。
总时间复杂度是 O ( n 2 ) O(n^2) O(n2)。 -
空间复杂度: O ( 1 ) O(1) O(1)。
这篇关于数组题目:可以被一步捕获的棋子数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




