[转]伽罗华域

GF(2^m)域

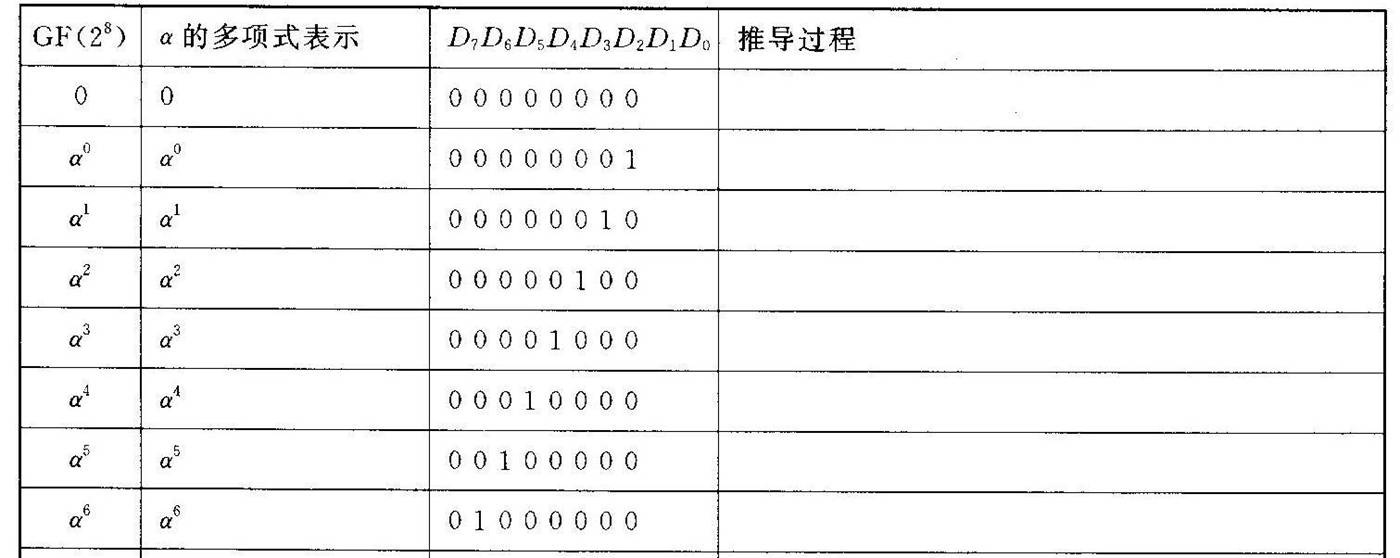
当m=8时，本原多项式为P(x) = x⁸ + x⁴ +x³ + x² + 1 .

这个很重要，因为一切化解都来源与此式。

在伽罗华域中,加法等同于对应位异或,所以

现在把α定义为P(x) = 0的根，即
　　　　α⁸＋α⁴＋α³＋α²＋1 = 0
　　　　即可以得到 α⁸=α⁴＋α³＋α²＋1

接着先给出下表付推导过程

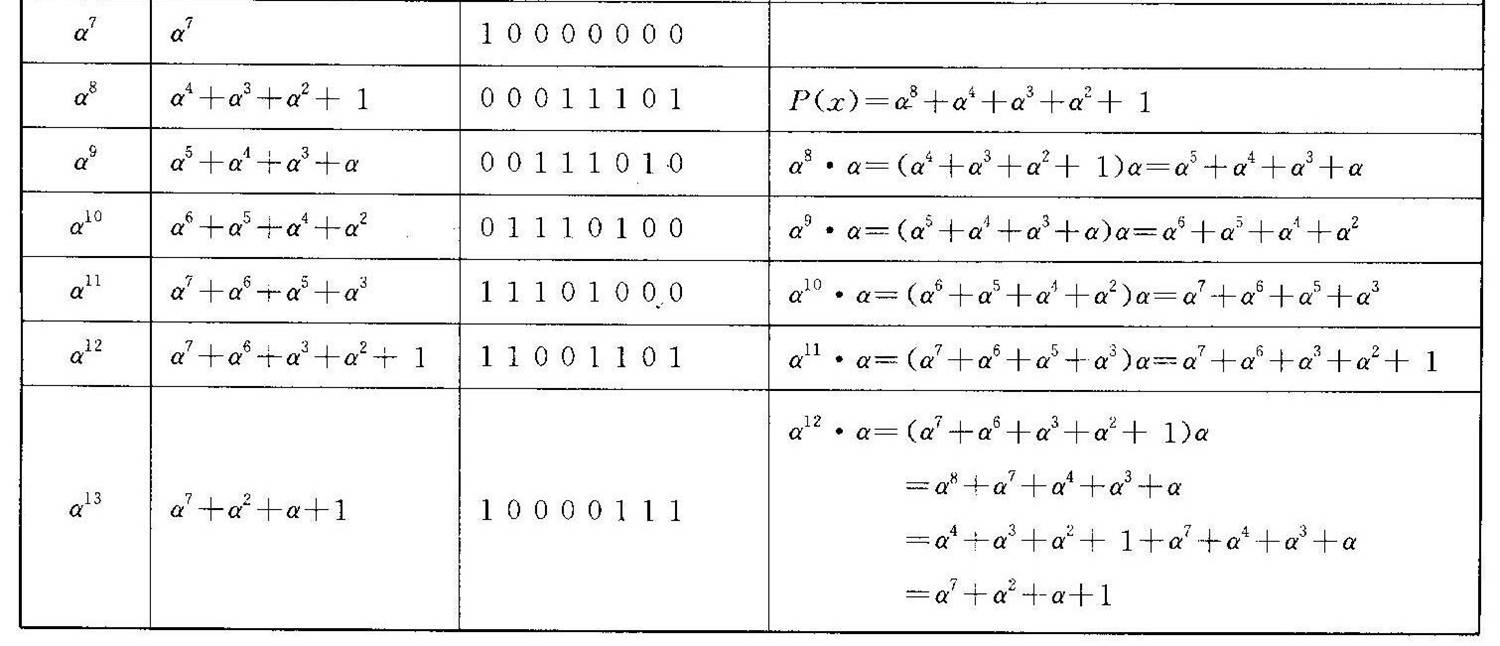
 下面就按以下规则进行乘法运算 

0=000   就是0   
  1=001   就是1   
  2=0010就是x+0=x   
  3=0011就是x+1   
  4=00100就是x^2   
  然后对于两个变量   
  u,v   
  可以先计算两个对应多项式的乘积（需要注意的是加法是模2的，或者说是异或运算），   
  比如   
  3*7=(x+1)*(x^2+x+1)=x*x^2+x*x+x+x^2+x+1=x^3+1   (模2运算中x+x=0   and   x^2+x^2=0)   
  所以3*7=9   
  在乘积得出来的多项式次数大于7时，我们需要对多项式在GF(2)上关于h(x)求余数，也就是   
  129*5=(x^7+1)*(x^2+1)=x^9+x^7+x^2+1   
  将上面的函数加上x*h(x)可以消去x^9,（其实就是手工除法过程，只是现在每一次商总是0或1），所以   
  129*5=x^9+x^7+x^2+1+x^9+x^5+x^4+x^3+x=x^7+x^5+x^4+x^3+x^2+x+1   
  =0010111111=191