本文主要是介绍洛谷P2437 蜜蜂路线 (递推+大数加法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述
一只蜜蜂在下图所示的数字蜂房上爬动,已知它只能从标号小的蜂房爬到标号大的相邻蜂房,现在问你:蜜蜂从蜂房 mm 开始爬到蜂房 nn,m<nm<n,有多少种爬行路线?(备注:题面有误,右上角应为 n-1n−1)
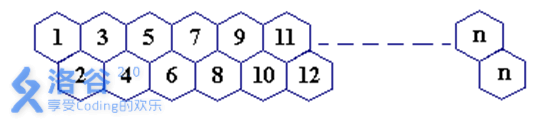
输入格式
输入 m,nm,n 的值
输出格式
爬行有多少种路线
输入输出样例
输入 #1
1 14输出 #1
377说明/提示
对于100%的数据 1<=M,N≤1000
思路:
类似于斐波那契数列的求解,一个状态可能是上一个状态走两步到达的,也可能是上一个状态走一步到达的,可以得到递推公式为DP[i]=DP[i-1]+DP[i-2](和斐波那契数列递推公式一样)。本题求出的是从第n个状态到第m个状态的走法,实际上就是求第m-n+1项斐波那契数列。
易错点:1<=n-m+1<=1000,最大是求斐波那契数列的第1000项,会爆longlong,因此需要使用大数加法。
#include<bits/stdc++.h>
using namespace std;
int m,n;
string dp[1100];//大数加法
string ADD(string a,string b)
{string temp;//将字符串反转,便于运算reverse(a.begin(),a.end());reverse(b.begin(),b.end());int t,c=0;//因为b是第i-2项,a是第i-1项,第i-2项一定小于第i-1项,所以b的位数一定小于等于a的位数for(int i = 0;i<b.length();i++){t = a[i]-'0'+b[i]-'0'+c;c=t/10;t%=10;temp+=t+'0';}//如果a的位数大于b的位数,需要加上a多余的位数,加的过程中还需要考虑上一步计算时候的进位for(int i = b.length();i<a.length();i++){int t = a[i]-'0'+c;c = t/10;t%=10;temp+=t+'0';}//最后有进位的话加上进位if(c) temp+=c+'0';reverse(temp.begin(),temp.end());return temp;
}int main()
{cin>>n>>m;;dp[1]="1";dp[2]="1";for(int i = 3;i<=m-n+1;i++){dp[i]=ADD(dp[i-1],dp[i-2]);}cout<<dp[m-n+1]<<endl;return 0;
}
这篇关于洛谷P2437 蜜蜂路线 (递推+大数加法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





