题目描述
最近,afy 决定给 TOJ 印刷广告,广告牌是刷在城市的建筑物上的,城市里有紧靠着的 N 个建筑。afy 决定在上面找一块尽可能大的矩形放置广告牌。我们假设每个建筑物都有一个高度,从左到右给出每个建筑物的高度 H1,H2,…,HN,且 0<Hi<=1,000,000,000,并且我们假设每个建筑物的宽度均为 1。要求输出广告牌的最大面积。
输入格式
第一行是一个数 n (n<= 1000,000 )。
第二行是 n 个数,分别表示每个建筑物高度 H1,H2,…,HN,且 0<Hi<=1,000,000,000。
输出格式
输出文件共有一行,表示广告牌的最大面积。
样例数据 1
输入
6
5 8 4 4 8 4
输出
24
题目分析
以一段中最矮的建筑物高度为高,向两边延展,直到有比其矮的建筑物时停止,用延展的宽度乘上高就是这一段的矩形面积,那么最终的答案就为$ans = max\{$以i为最低点延展得到的矩形面积$\} (1 ≤ i ≤ n )$。当然我们也不能这样每次向两边延展,复杂度爆棚。
单调队列:先考虑向左延展,维护一个单调递增的序列, 每次加入新的元素,就把队列中大于等于新元素的都删掉,因为他们的高度都大于等于当前的新元素,那么这个新元素一定就能延展到大于等于新元素的最小元素的延展边缘,也就是
l[i] = i; while(tot && h[que[tot]] >= h[i]) l[i] = l[que[tot--]];que[++tot] = i;
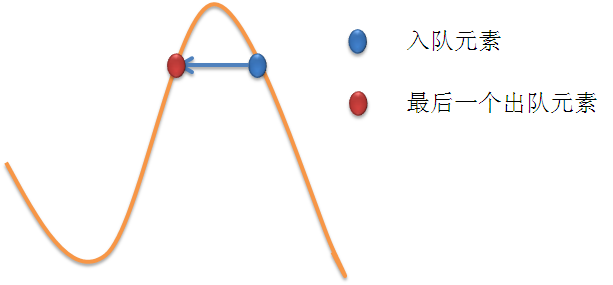
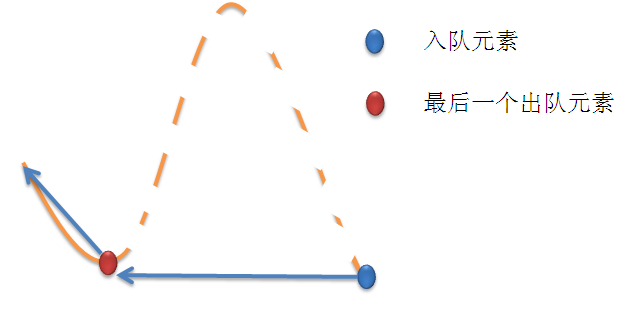
向右延展同理,只需将序列倒着做一次就行了。
code
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<algorithm> #include<cmath> #include<vector> using namespace std;const int N = 1e6 + 5; int n, h[N], l[N], r[N]; int que[N], tot;inline int read(){int i = 0, f = 1; char ch = getchar();for(; (ch < '0' || ch > '9') && ch != '-'; ch = getchar());if(ch == '-') f = -1, ch = getchar();for(; ch >= '0' && ch <= '9'; ch = getchar())i = (i << 3) + (i << 1) + (ch - '0');return i * f; }inline void wr(long long x){if(x < 0) putchar('-'), x = -x;if(x > 9) wr(x / 10);putchar(x % 10 + '0'); }int main(){n = read();for(int i = 1; i <= n; i++) h[i] = read();que[tot = 1] = l[1] = 1;for(int i = 2; i <= n; i++){l[i] = i;while(tot && h[que[tot]] >= h[i]) l[i] = l[que[tot--]];que[++tot] = i;}long long ans = -1;que[tot = 1] = r[n] = n;for(int i = n - 1; i >= 1; i--){r[i] = i;while(tot && h[que[tot]] >= h[i]) r[i] = r[que[tot--]];que[++tot] = i;ans = max(ans, 1LL * (r[i] - l[i] + 1) * h[i]);}wr(ans);return 0; }









