本文主要是介绍相同周长的图形,面积最大者是圆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
等周定理[编辑]
等周定理,又称等周不等式,是一个几何中的不等式定理,说明了欧几里得平面上的封闭图形的周长以及其面积之间的关系。其中的“等周”指的是周界的长度相等。等周定理说明在周界长度相等的封闭几何形状之中,以圆形的面积最大;另一个说法是面积相等的几何形状之中,以圆形的周界长度最小。这两种说法是等价的。它可以以不等式表达:若 为封闭曲线的周界长,
为封闭曲线的周界长, 为曲线所包围的区域面积,
为曲线所包围的区域面积, 。
。
虽然等周定理的结论早已为人所知,但要严格的证明这一点并不容易。首个严谨的数学证明直到19世纪才出现。之后,数学家们陆续给出了不同的证明,其中有不少是非常简单的。等周问题有许多不同的推广,例如在各种曲面而不是平面上的等周问题,以及在高维的空间中给定的“表面”或区域的最大“边界长度”问题等。
在物理中,等周问题和跟所谓的最小作用量原理有关。一个直观的表现就是水珠的形状。在没有外力的情况下(例如失重的太空舱里),水珠的形状是完全对称的球体。这是因为当水珠体积一定时,表面张力会迫使水珠的表面积达到最小值。根据等周定理,最小值是在水珠形状为球状时达到。
历史[编辑]


平面上的等周问题是等周问题最经典的形式,它的出现可以追溯到很早以前。这个问题可以被表述为:在平面上所有周长一定的封闭曲线中,是否有一个围成的面积最大?如果有的话,是什么形状?另一种等价的表述是:当平面上的封闭曲线围成的面积一定时,怎样的曲线周长最小?
虽然圆看似是问题的表面答案,但证明此事实其实不易。首个接近答案的步骤出现在1838年——雅各·史坦纳以几何方法证明若答案存在,答案必然是圆形[1]。不久之后他的证明被其他数学家完善。
其方法包括证明了不完全凸的封闭曲线的话,能以“翻折”凹的部分以成为凸的图形,以增加面积;不完全对称的封闭曲线能以倾斜来取得更多的面积。圆,是完全凸和对称的形状。可是这些并不足以作为等周定理的严格证明。
1901年,赫尔维茨凭傅里叶级数和格林定理给出一个纯解析的证明。
证明[编辑]
以下给出一个较初等的证明[2],分5步。
设一条长度为P的封闭曲线围成的区域的最大面积为A,亦以A、P来标记该区域及其边界;那么该图形应当满足如下性质:
1、A是一个凸区域。
- 假使不然,A是一个凹区域。那么根据定义,可以在P内找到两个点M和N,使其连线MN有一部份M'N'不包含于A的内部。然而如以M'N'替换掉原来的那段弧,则周长将减少,面积将增加,从而将新图形扩大若干倍后得到一个同样周长,面积比A大的区域。矛盾。
2、凡平分周长P的弦必平分面积A。
- 如果一弦MN平分P而将A分为大小不同的两部份
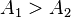 ,那么去掉
,那么去掉 而将
而将 对MN做对称,则可得到一个周长仍然等于P而面积等于
对MN做对称,则可得到一个周长仍然等于P而面积等于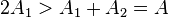 的区域,矛盾。
的区域,矛盾。
3、凡平分A的弦,无论方向,长度相等。
- 如果不然,不妨设两弦MN和M'N'均平分面积A而MN>M'N'。那么分别选取MN及其任一侧的曲线(半个P,不妨记为
 ),以及M'N'及其任一侧的区域(另行划分的半个P,记为
),以及M'N'及其任一侧的区域(另行划分的半个P,记为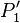 ),并粘合在一起使得M'N'落在MN上,M与M'重合。
),并粘合在一起使得M'N'落在MN上,M与M'重合。 - 此时,新的图形仍然满足周长为P,面积为A的性质,且由于MN>M'N',N'应落于MN之间。
- 以M为中心,分别对
 和
和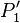 做
做 和
和 倍的放缩,使两曲线的终端吻合(即N和N'经过变换之后重合,记为
倍的放缩,使两曲线的终端吻合(即N和N'经过变换之后重合,记为 ),得到两个分别与原区域相似的区域
),得到两个分别与原区域相似的区域 和
和 。适当调整
。适当调整 和
和 的值,使曲线
的值,使曲线 的周长仍为P。
的周长仍为P。 - 此时
 和
和 的长度分别等于
的长度分别等于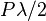 和
和 ,所围的面积分别等于
,所围的面积分别等于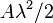 和
和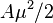 ;并且由于MN和MN'经过放缩后重合,有
;并且由于MN和MN'经过放缩后重合,有 。
。
- 此时
- 由于曲线
 的周长仍为P,故
的周长仍为P,故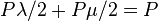 ,从而
,从而 ;而由
;而由 知
知 。
。 - 所以,
 的面积为
的面积为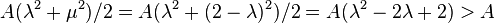 ,与A最大矛盾。
,与A最大矛盾。
4、若MN平分A,O为MN中点,那么对P上任意一点R,都有OM=ON=OR。
- 以O为中心,做MRN的中心对称图形,R对称到R';那么图形MR'NRM的周长为P,面积为A。由第3步知MN和RR'的长度应该相等,而O也是RR'的中点,故得结论。
5、由于O到P上任意一点的距离都相等,所以P是圆。
参考来源[编辑]
- ^ J. Steiner, Einfacher Beweis der isoperimetrischen Hauptsätze, J. reine angew Math. 18, (1838), pp. 281–296; and Gesammelte Werke Vol. 2, pp. 77–91, Reimer, Berlin, (1882).
- ^ 福原満洲雄、山中健,変分学入门,朝仓书店,1978.3.
这篇关于相同周长的图形,面积最大者是圆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!