本文主要是介绍奇怪这篇IEEE某transactions求张成子空间的基，为何这么古怪？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
今天早上打开小木虫看到有人问下面的问题：
如图中给出b1,b2，那么他这个b3,b4定义是什么意思。如何推到计算出来的
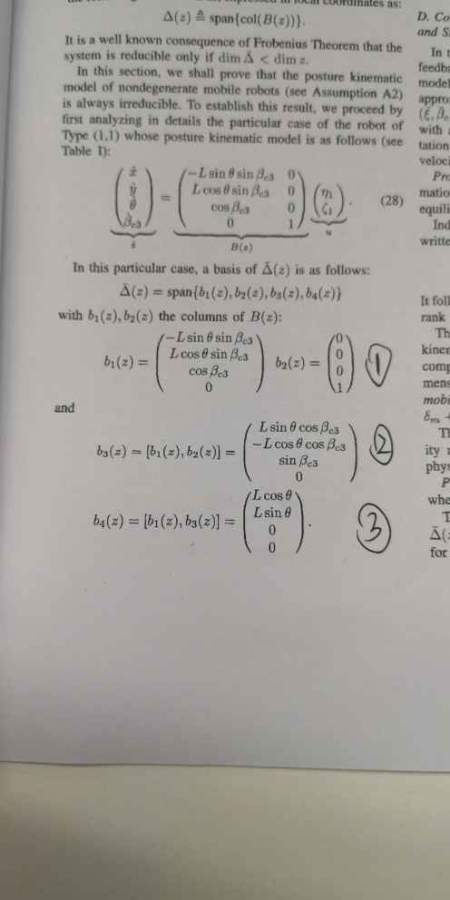
因为图不太清楚，我就用Google, 取其中一句话，In this sectin we shall prove that the posutre kinematic model of nondegenerate mobile robots 加双引号，搜了一下，找到唯一定位的这篇文章， 是一篇IEEE Transactions 刊物1996年的论文，PDF不清晰但可以下载。
针对这个问题，我思考了下，因为是四维向量，似乎的确没有太好的方法表示"[*]"里面的这种计算，不过“正交补”这种子空间应该是有的、在Mathematica里面对应·NullSpace函数。计算了一下，得到的结果明显比论文里面给出的结果优越：
已知
b 1 ( z ) = ( − L ⋅ sin θ ⋅ sin β L ⋅ cos θ ⋅ sin β cos β 0 ) , b 2 ( z ) = ( 0 0 0 1 ) b_1(z)=\left(\begin{array}{c} -L \cdot \sin \theta\cdot \sin \beta \\ L \cdot \cos \theta\cdot \sin \beta \\ \cos \beta \\ 0 \\ \end{array}\right),\quad b_2(z)=\left(\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ \end{array}\right) b1(z)=⎝⎜⎜⎛−L⋅sinθ⋅sinβL⋅cosθ⋅sinβcosβ0⎠⎟⎟⎞,b2(z)=⎝⎜⎜⎛0001⎠⎟⎟⎞
它们两个的正交补的正交基、容易得到是下面两个列向量：
b 3 ∗ ( z ) = ( 1 sin θ cos β sin β L 0 1 0 ) , b 4 ∗ ( z ) = ( cos θ sin θ 1 0 0 ) b^*_3(z)=\left( \begin{array}{c} \dfrac{\dfrac{1}{\sin\theta} \dfrac{\cos \beta}{\sin\beta}}{L} \\[15pt] 0 \\[10pt] 1 \\[10pt] 0 \\ \end{array} \right) , \quad b^*_4(z)=\left( \begin{array}{c} \dfrac{\cos\theta}{\sin \theta} \\[15pt] 1 \\[10pt] 0 \\[10pt] 0 \\ \end{array} \right) b3∗(z)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛Lsinθ1sinβcosβ010⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞,b4∗(z)=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛sinθcosθ100⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞
整理成：
b 3 ( z ) = ( cos β 0 L sin θ ⋅ sin β 0 ) ( Not good, eliminated ) ≈ ( − sin θ cos β cos θ cos β − L sin β 0 ) , b 4 ( z ) = ( cos θ sin θ 0 0 ) b_3(z)={\color{blue}{\left( \begin{array}{c} \cos\beta \\[15pt] 0 \\[10pt] L\sin \theta\cdot\sin\beta \\[10pt] 0 \\ \end{array} \right)}}\left(\color{red}\text{Not good, eliminated}\right) \approx \left(\begin{array}{c} -\sin \theta \cos \beta \\[10pt] \cos \theta \cos\beta \\[10pt] -L \sin\beta \\[10pt] 0\\ \end{array} \right), \quad b_4(z)=\left( \begin{array}{c} {\cos\theta} \\[15pt] \sin\theta \\[10pt] 0 \\[10pt] 0 \\ \end{array} \right) b3(z)=⎝⎜⎜⎜⎜⎜⎜⎜⎛cosβ0Lsinθ⋅sinβ0⎠⎟⎟⎟⎟⎟⎟⎟⎞(Not good, eliminated)≈⎝⎜⎜⎜⎜⎜⎜⎜⎛−sinθcosβcosθcosβ−Lsinβ0⎠⎟⎟⎟⎟⎟⎟⎟⎞,b4(z)=⎝⎜⎜⎜⎜⎜⎜⎜⎛cosθsinθ00⎠⎟⎟⎟⎟⎟⎟⎟⎞
这样一来 b 1 ( z ) , b 2 ( z ) , b 3 ( z ) , b 4 ( z ) b_1(z), b_2(z),b_3(z),b_4(z) b1(z),b2(z),b3(z),b4(z) 是一组正交基。不知道原作者为什么得到那么奇怪的一个 b 3 ( z ) b_3(z) b3(z)？
这篇关于奇怪这篇IEEE某transactions求张成子空间的基，为何这么古怪？的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
