中兴2018届应届生在线编程测验0829 数学家排成平行四边形问题

问题:

欧几里得,毕达哥拉斯,帕斯卡和蒙特打算到公园游玩.将公园可视为N(行)*M(列)个位置.帕斯卡,蒙特和欧几里得站在3个不同的位置.毕达哥拉斯是最后一个到达公园,他决定站在一个能让四个点形成一个平行四边形的位置.欧几里得和蒙特的位置则形成平行四边形的对角线.

编写一个算法,帮助毕达哥拉斯决定站在公园的什么位置.

输入

函数输入包括七个参数

vector<int> toCompleteParrelogram(int rows, int cols, char** p, int euclidX, int euclidY, int monteX, int monteY)

分别代表行数,列数,公园的符号矩阵,欧几里得X坐标,欧几里得Y坐标,蒙特X坐标,蒙特Y坐标.

p中符号"+"代表人的位置,"-"代表空地.

输出

返回一个整数列表,表示毕达哥拉斯完成平行四边形应站的X和Y的坐标.

用例1

输入:

4,8

--------

-+------

--------

-+----+-

输出: 

2 7 

用例2

输入:

----

-+--

+---

----
--+-

输出:

4 4

分析:如图四个点代表四位数学家的位置,标号为名字的首字母大写.由平行四边形的性质可知.

EP = MB

MP = BE

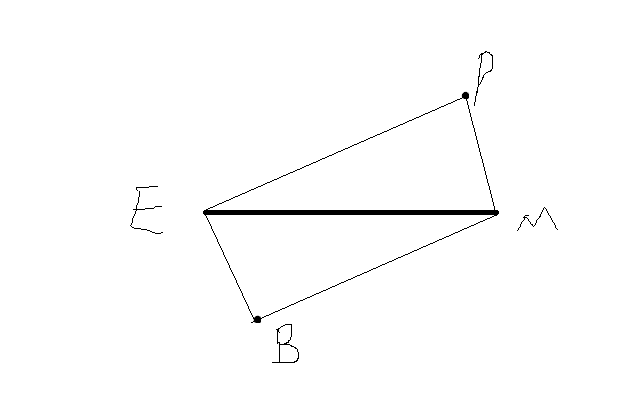
题中又有欧几里得和蒙特的位置则形成平行四边形的对角线.以上两点还不能保证这些

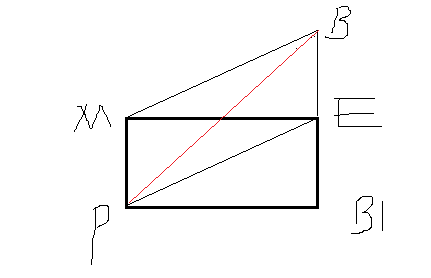
比如下图

图中的矩形MEB1P也满足上述两个条件,而实际上满足题意的是MBEP.所以还要加一个条件,BP的中点和ME的中点重合.

下面是参考程序:

#include <iostream>
#include <vector>
using namespace std;int squaredistance(int row1, int col1,int row2, int col2) //两个位置之间距离的平方
{return (row1 - row2)*(row1 - row2) + (col1 - col2)*(col1 - col2);
}double MidPoint(int coord1, int coord2) //两个坐标的中点
{return 1.0 / 2 * (coord1 + coord2);
}vector<int> toCompleteParrelogram(int rows, int cols, char** p, int euclidX, int euclidY, int monteX, int monteY)
{int pasikX, pasikY, bidaX, bidaY;int i, j;//找出第三个人的坐标vector<int> ivec;for (i = 0; i < rows; i++){for (j = 0; j < cols; j++){if (*(*(p + i) + j) == '+')        //引用元素的格式{if ((i + 1 != euclidX || j + 1 != euclidY) && (i + 1 != monteX || j + 1 != monteY))    //数组下标从0开始,而位置从1开始,所以加上1{                                                                                    //对于二维的点,有一维不一样,两者就是不一样的pasikX = i + 1;pasikY = j + 1;}}}}//求出第四个人的位置for (i = 0; i < rows; i++){for (j = 0; j < cols; j++){//两条对边相等EP = MB  MP = BEif ( squaredistance(euclidX, euclidY, pasikX, pasikY) == squaredistance(monteX, monteY, i + 1, j + 1) && squaredistance(euclidX, euclidY, i + 1, j + 1) == squaredistance(monteX, monteY, pasikX, pasikY)){//对角线的中点重合   if (MidPoint(euclidX, monteX) == MidPoint(pasikX, i+1) && MidPoint(euclidY, monteY) == MidPoint(pasikY, j + 1)){bidaX = i + 1;bidaY = j + 1;ivec.push_back(bidaX);ivec.push_back(bidaY);return ivec;}}}}cout << "无解" << endl;    //当所有点都判断完仍没有return回去,则代表无解.return ivec;    //仍要return
}int main()
{char *a[] = { "--------", "-+------", "--------", "-+----+-" };//案例一
//     char *a[] = { "----", "-+--", "+---", "----" ,"--+-"};//案例二char **pp = a;vector<int>ivec1(toCompleteParrelogram(4, 8, pp,2,2,4,7));//案例一//     vector<int>ivec1(toCompleteParrelogram(5, 4, pp, 2, 2, 5, 3));案例二. 初始化时可以这样,但不可分成两步.因为那就是赋值了.if (ivec1.size() == 2){cout << ivec1[0]<< " " << ivec1[1] << endl;}return 0;
}