损失函数中为什么要用Log？

参考：机器学习中损失函数常用log的用意_损失函数为什么用log_小妖精Fsky的博客-CSDN博客

Loss 在使用似然函数最大化时，其形式是进行连乘，但是为了便于处理，一般会套上log，这样便可以将连乘转化为求和，由于log函数是单调递增函数，因此不会改变优化结果。

极大似然估计中取对数的原因：取对数后，连乘可以转化为相加，方便求导，这是因为对数函数的求导更加简单，对数函数的导数比原函数更容易计算和优化；除此之外对数函数 ln为单调递增函数，不会改变似然函数极值点。

以下是个人拙见：

首先在分类中为什么会用到似然函数的概念？

我们在对一个图片进行分类（假设是每个图片只有一个类别）时，例如：我们通过模型得到了每个样本对应真实类别的概率值，即（i=0,1,2...,n；n是样本个数），假设有k个类别，但我们只取每个样本对应其真实类别的那个概率。

我们使用极大似然估计反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。即

最大化这个概率。即，我们希望找到极大值点，使得概率最大化，这就需要求偏导。

但往往连乘不容易求导。

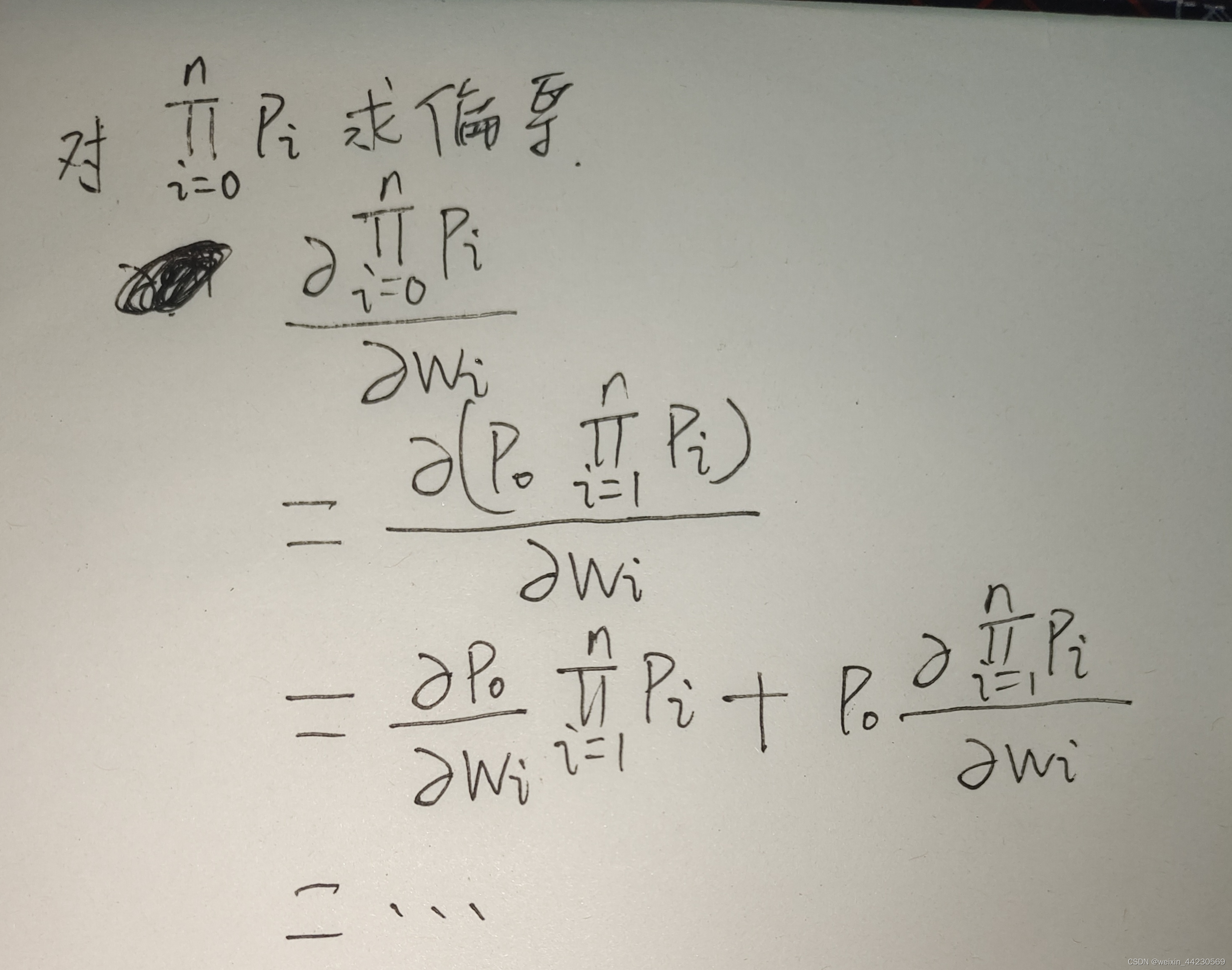
我们分析似然函数，其值在0到1之间，而且越接近于1说明分类的效果越好，越接近于0说明分类的效果越差。与此同时-log函数在0到1区间单调递减，且大于等于0，假设我们取对数似然后，那么对数值越大说明越接近于0，对数值越小越接近于1，即（注意这里是不同样本对应其真实类别的概率）。我们希望能够找到使得对数值最小的一组参数，即

 这样求导比较容易一些。

取对数似然除了求导方便之外，还有其他的好处吗?我们知道float32的数值范围是：

 连乘容易导致数值溢出，假设我们有100个样本，每个样本分类的真实概率值为0.1，那么,而负对数似然就不会有这个问题，当存在单个样本真实概率溢出的情况下，会出现数值溢出的问题，也是半精度计算中经常出现的loss nan的问题。

取对数似然和softmax是因为可以消掉吗？

个人认为答案是否定的。

首先我们思考为什么要用softmax，假设我们不用softmax，模型最后的输出有可能是[-0.1, -0.1, 0.1](三分类)，也有可能是[10, 9.9,9.9],我们使用极大似然估计来分析，第二个输出的值大，它的置信度应该很高，但事实并非如此。我们使用softmax的根本原因是将其转化为0到1之间的概率，且所有的值加起来等于 1。

softmax 和 cross-entropy 本来没有太大的关系，只是把两个放在一起实现的话，算起来更快，也更数值稳定。