本文主要是介绍【POJ No. 3278】抓住那头牛 Catch That Cow,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【POJ No. 3278】抓住那头牛 Catch That Cow
POJ题目地址
【题意】
约翰希望立即抓住逃亡的牛。当前约翰在节点N ,牛在节点K (0≤N , K ≤100 000)时,他们在同一条线上。约翰有两种交通方式:步行和乘车。如果牛不知道有人在追赶自己,原地不动,那么约翰需要多长时间才能抓住牛?
- 步行:约翰可以在一分钟内从任意节点X 移动到节点X -1或X+1。
- 乘车:约翰可以在一分钟内从任意节点X 移动到节点2×X 。
【输入输出】
输入:
两个整数N 和K 。
输出:
单行输出约翰抓住牛所需的最短时间(以分钟为单位)。
【样例】

提示: 在输入样例中抓住牛的最快方法是沿着路径5-10-9-18-17前进,需要4分钟。
【思路分析】
可以采用深度优先搜索和广度优先搜索两种方法解决。
【算法设计】
① 深度优先搜索方法
根据输入样例,约翰在5的位置,牛在17的位置。约翰可以先乘车到10,步行退回到9,然后乘车到18,步行退回到17,抓到牛,一共4步。
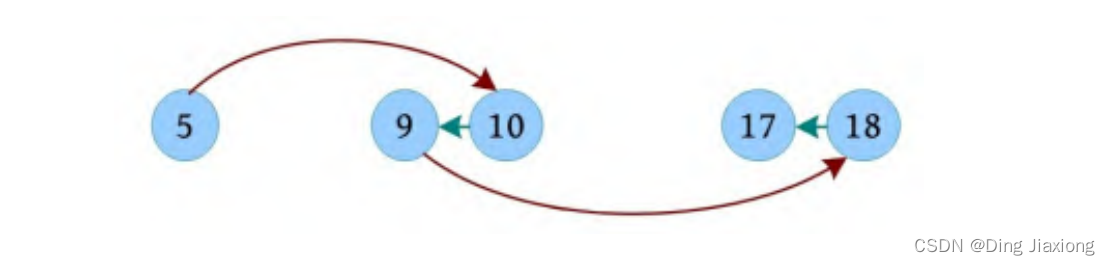
假设约翰和牛的位置分别为n 和k ,则求解步骤如下:
-
如果n =0,则先走1步到1,n =1,否则无法乘车,因为0的两倍还是0。
-
进行深度优先搜索,dfs(t )表示求解约翰从初始位置n 到达位置t 的最小步数。
- 如果t ≤n ,因为不可以向后乘车,只能一步一步地后退,则需要n -t 步。
- 如果t 为偶数,则比较从t/2 向前乘车到t、 从n 一步一步向前走到t ,采用哪种方案使得步数最少,取最小值。第1种方案的步数为从初始位置到达t/2 的步数dfs(t /2)加上1次乘车所需步数,第2种方案的步数为t -n 。
- 如果t 为奇数,则比较从t -1向前1步到t (步数为dfs(t-1)+1)、从t +1向后1步到t (步数为dfs(t +1)+1),采用哪种方案使得步数最少,取最小值。
int dfs(int t){if(t <= n){return n - t;}if(t % 2 == 1){return min(dfs(t + 1) + 1, dfs(t - 1) + 1);}else{return min(dfs(t / 2) + 1, t - n);}
}
② 广度优先搜索算法
- 如果k ≤n ,因为不可以向后乘车,只能一步一步地后退,则需要n -k 步,否则执行步骤2。
- 从当前节点出发进行广度优先搜索,每个节点都可以扩展3个位置,判断该位置是否为牛的位置,如果是,则返回走过的步数;否则,判断位置是否有效(未超界且未访问),如果是,则将步数加1,并将位置入队。
- 如果队列不空,则一直进行广度优先搜索,直到找到牛的位置。
【完美图解】
从约翰的位置5出发进行广度优先搜索,节点5先扩展3个位置,然后节点6、4、10扩展,如下图所示。
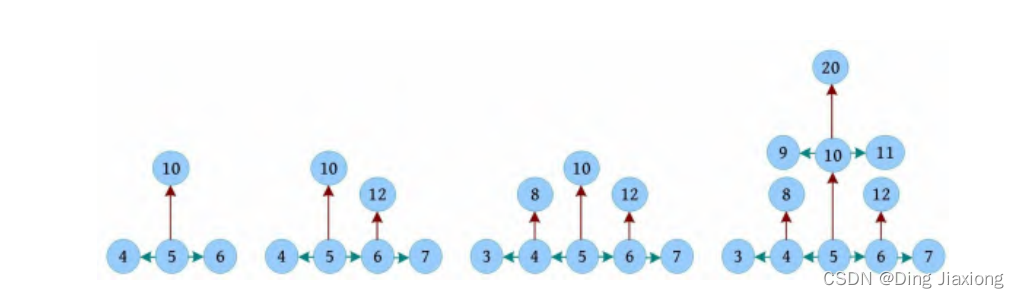
继续进行广度优先搜索,直到找到牛的位置,返回走过的距离。
从以上扩展可以看出,有很多无效搜索,效率比采用深度优先搜索要低。因为在一条直线上,所以采用深度优先搜索效果更好;如果在二维地图上,则采用广度优先搜索效果更好。
【算法实现】
#include<iostream>
#include<algorithm>using namespace std;
int n , k;int dfs(int t){if(t <= n){return n - t;}if(t % 2){return min(dfs(t + 1) + 1 , dfs(t - 1) + 1); }else{return min(dfs(t / 2) + 1 , t - n);}
}int main(){while(cin >> n >> k){int ans = 0;if(n == 0){ //特判 n = 1;ans = 1;}ans += dfs(k);cout << ans << endl;}return 0;
}

这篇关于【POJ No. 3278】抓住那头牛 Catch That Cow的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




