C语言数据结构之两道OJ题带你走近环形链表

本文主要是介绍C语言数据结构之两道OJ题带你走近环形链表，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

倘若南风知我意

莫将晚霞落黄昏

🎥烟雨长虹，孤鹜齐飞的个人主页

🔥个人专栏

🎥前期回顾-单链表

目录

环形链表

题目描述#

思路#

代码测试#

环形链表II

题目描述#

思路#

代码测试#

环形链表

题目链接：环形链表

题目描述#

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。
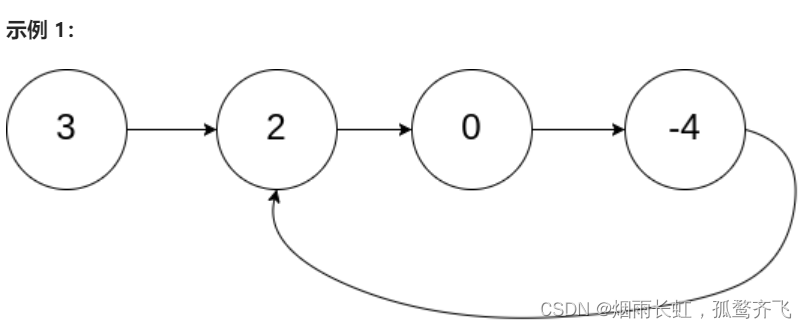
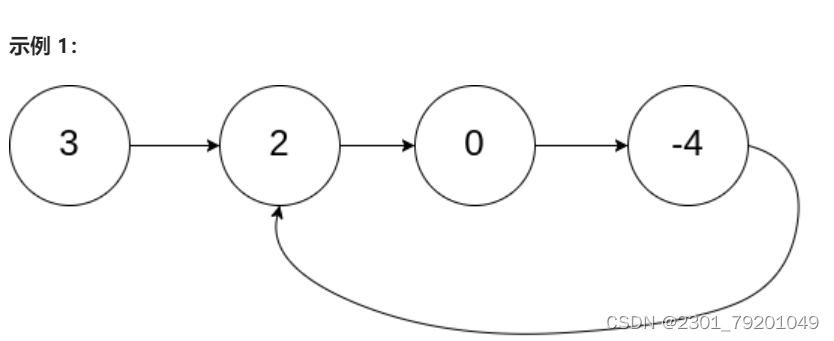
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
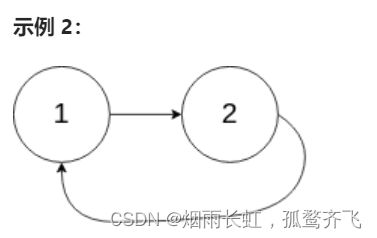
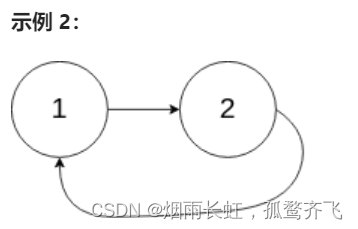
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
提示：

链表中节点的数目范围是 [0, ]
<= Node.val <=
pos 为 -1 或者链表中的一个 有效索引 。

思路#

快慢指针+追击问题：

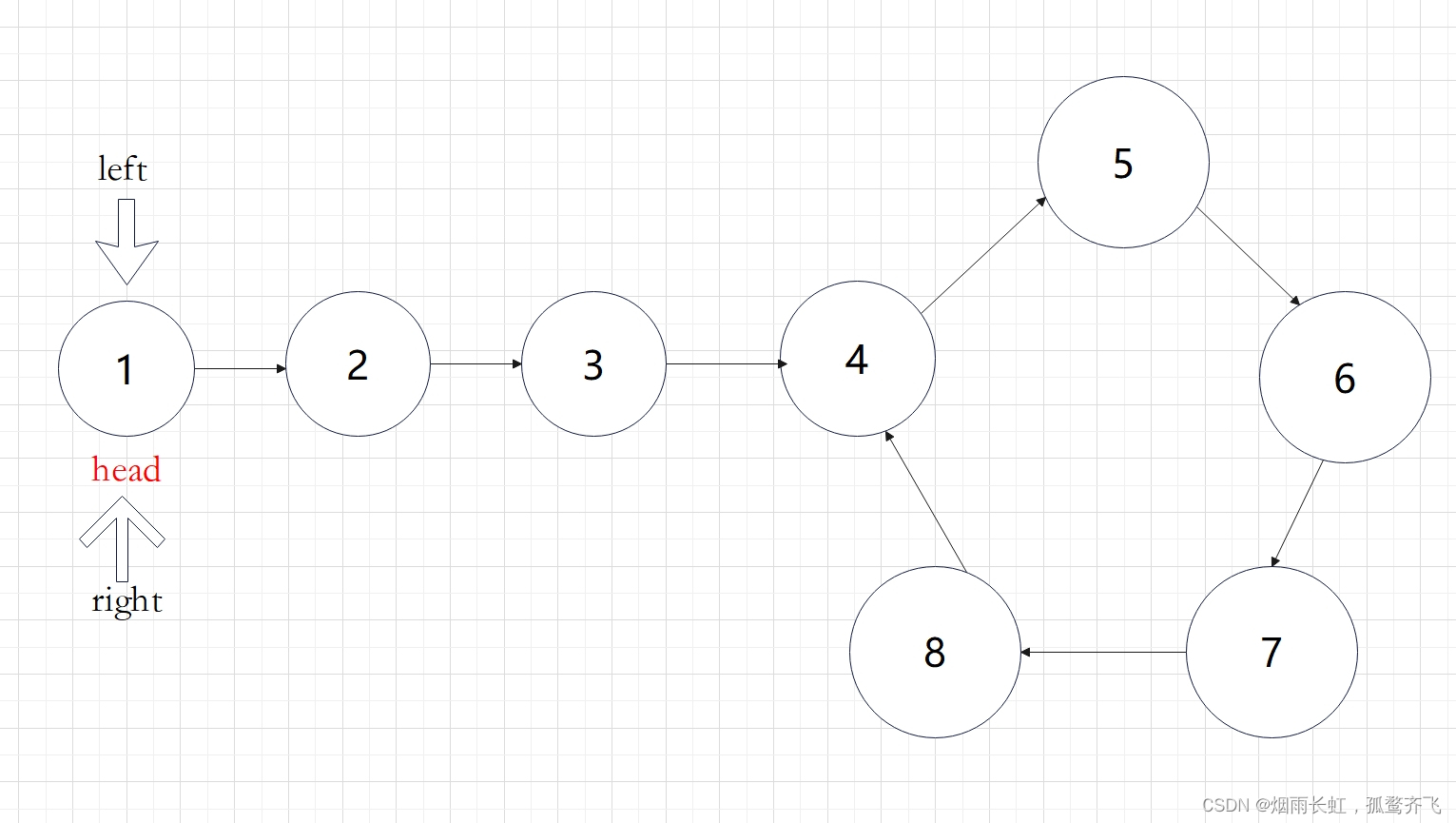
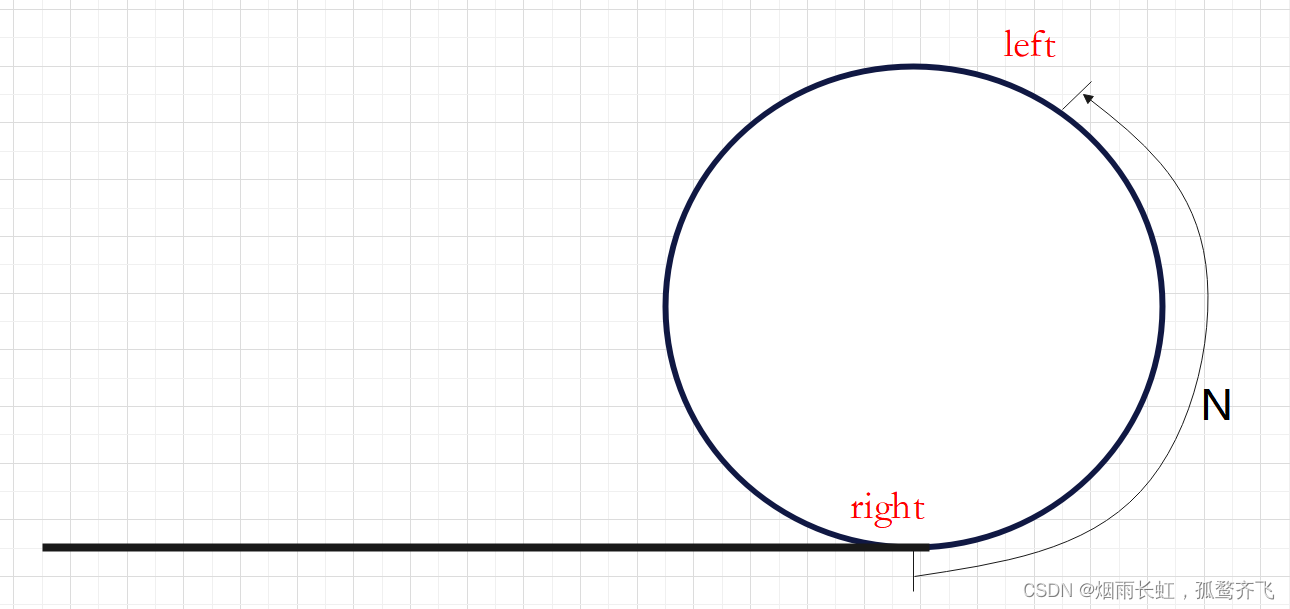
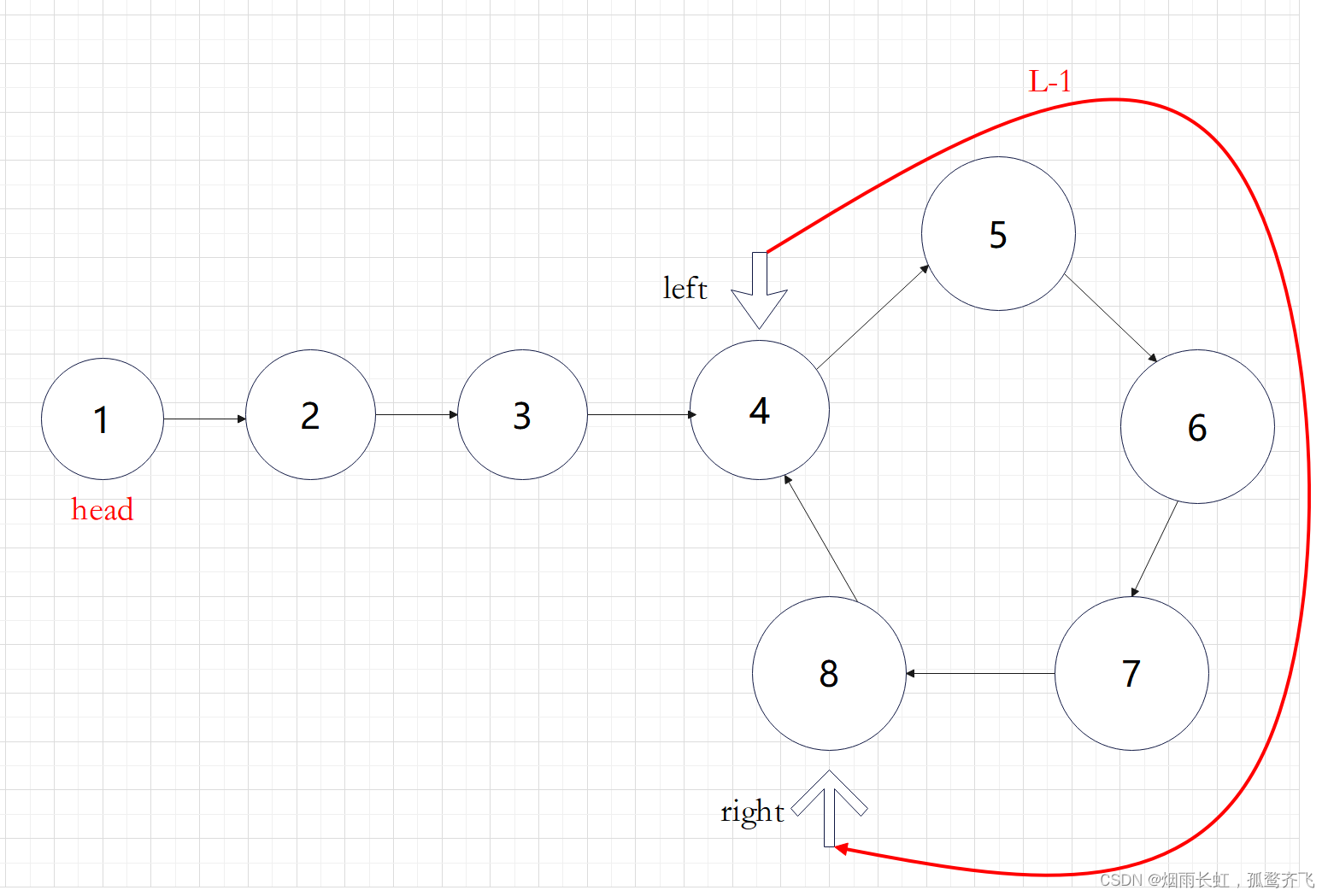
定义两个快慢指针在链表上移动，left 跑得快，right 跑得慢。当 left 和 right 从链表上的同一个节点开始移动时，如果该链表中没有环，那么 left 将一直处于 right 的前方；如果该链表中有环，那么 left 会先于 right 进入环，并且一直在环内移动。等到 right 进入环时，由于 left 的速度快，它一定会在某个时刻与 right 相遇，则链表中存在环。否则快指针 left 率先走到链表的末尾。

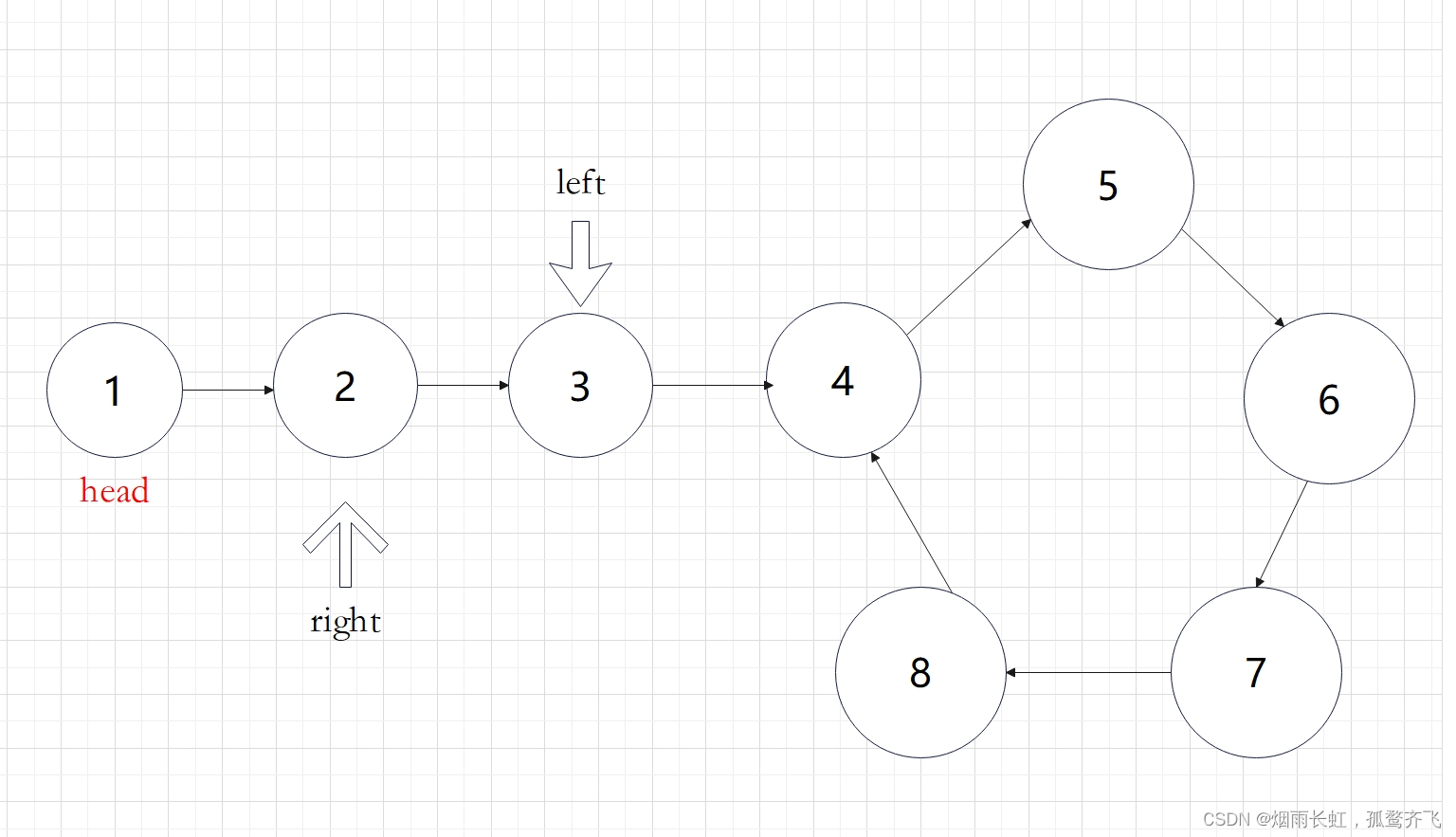
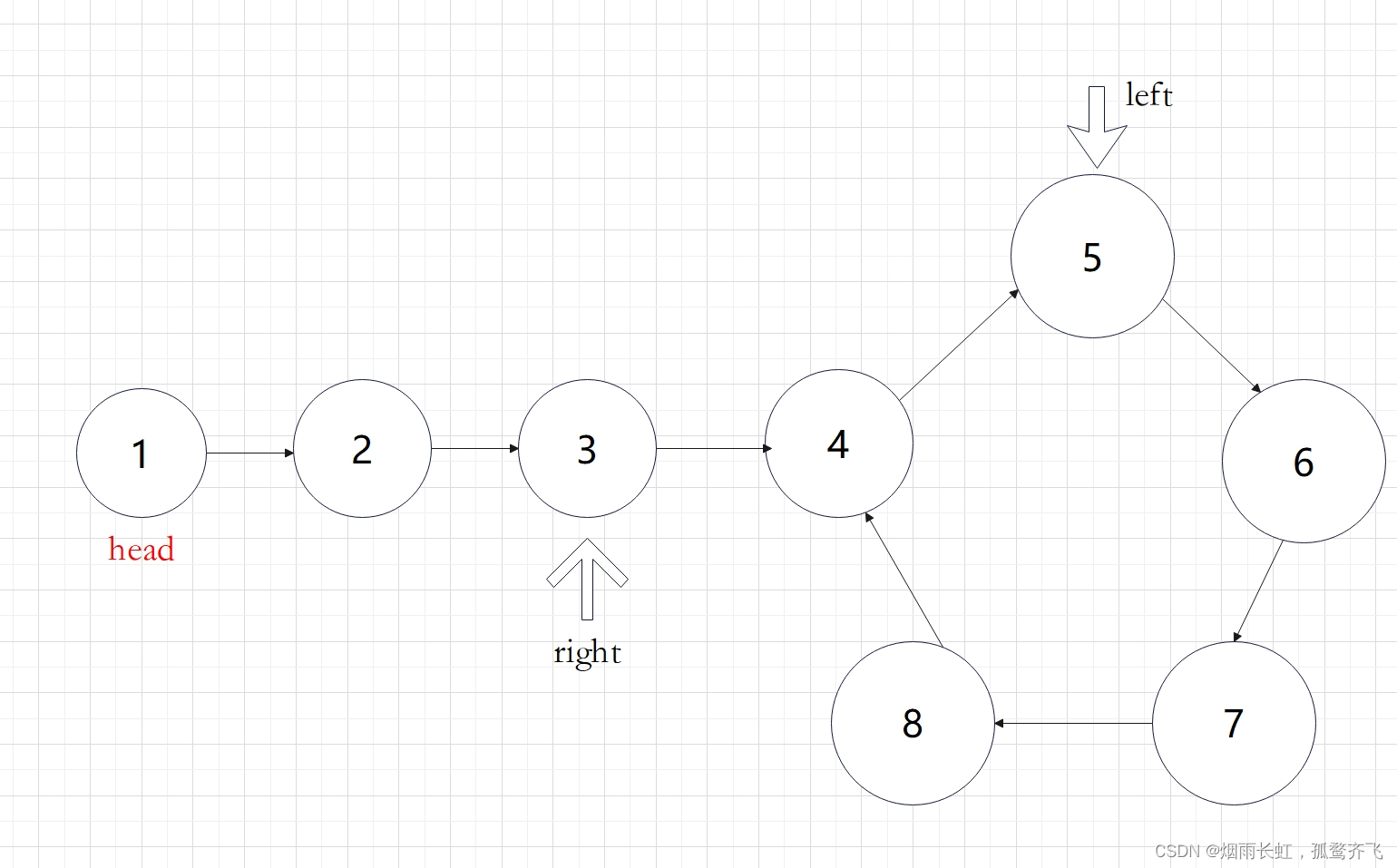
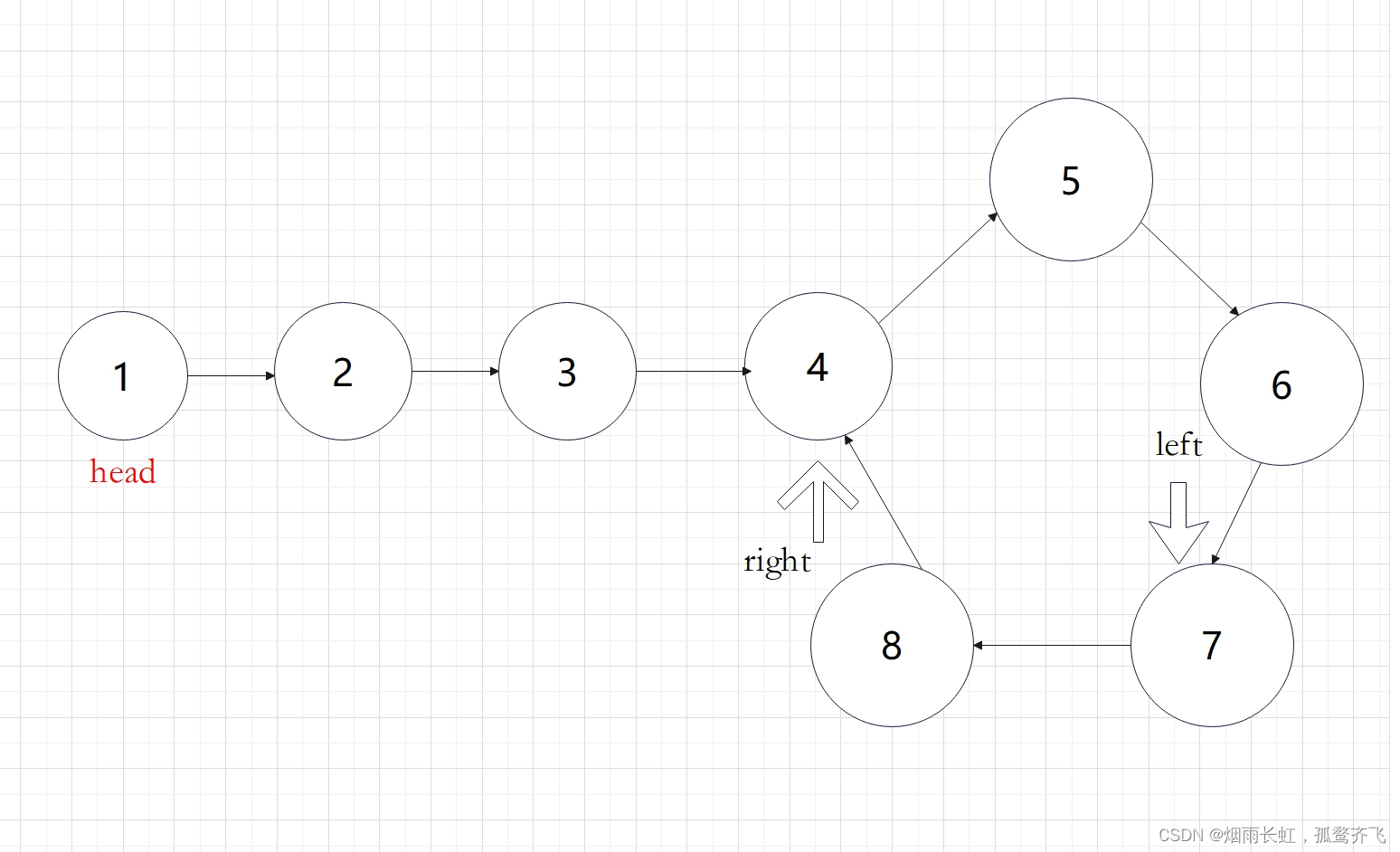
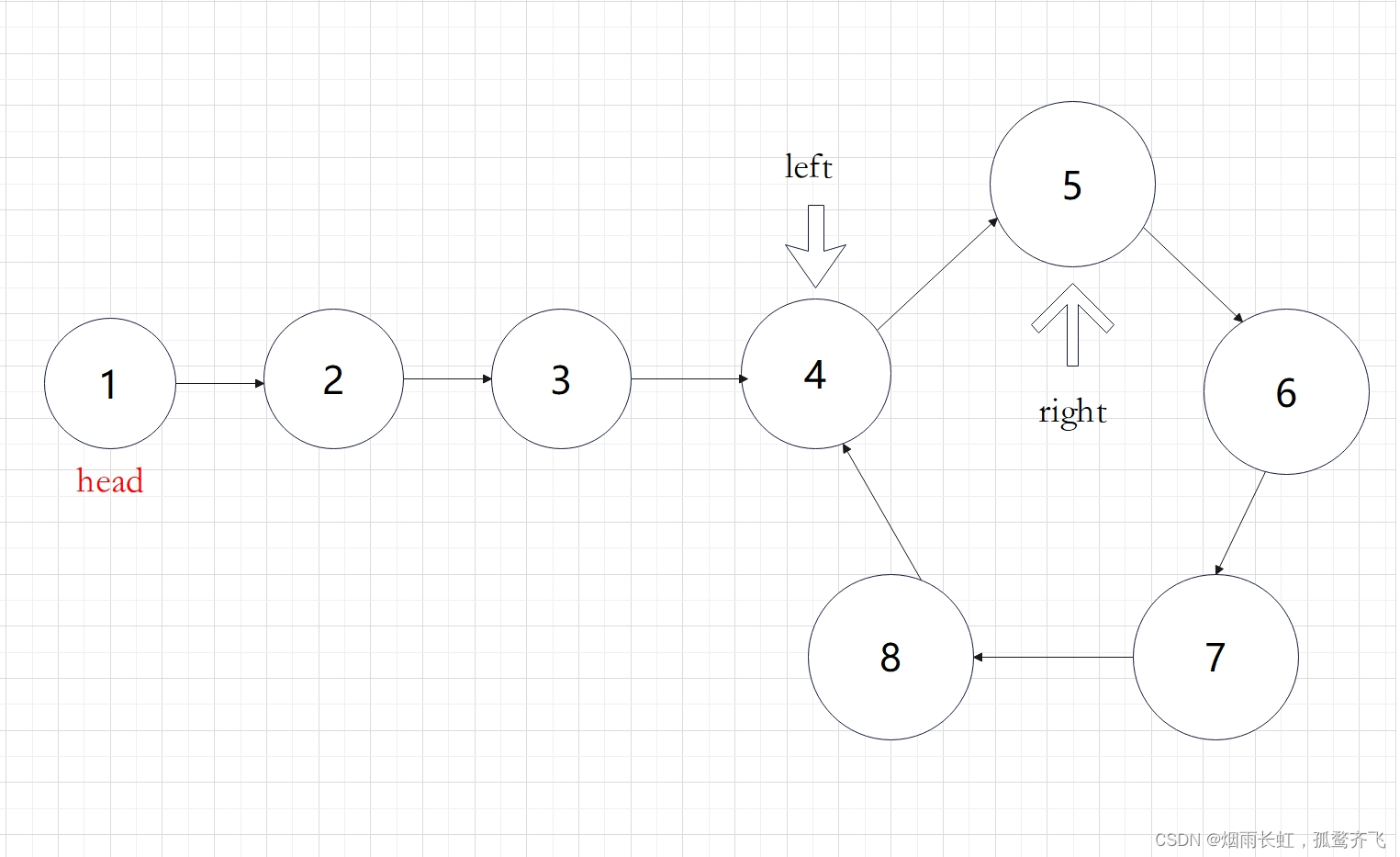
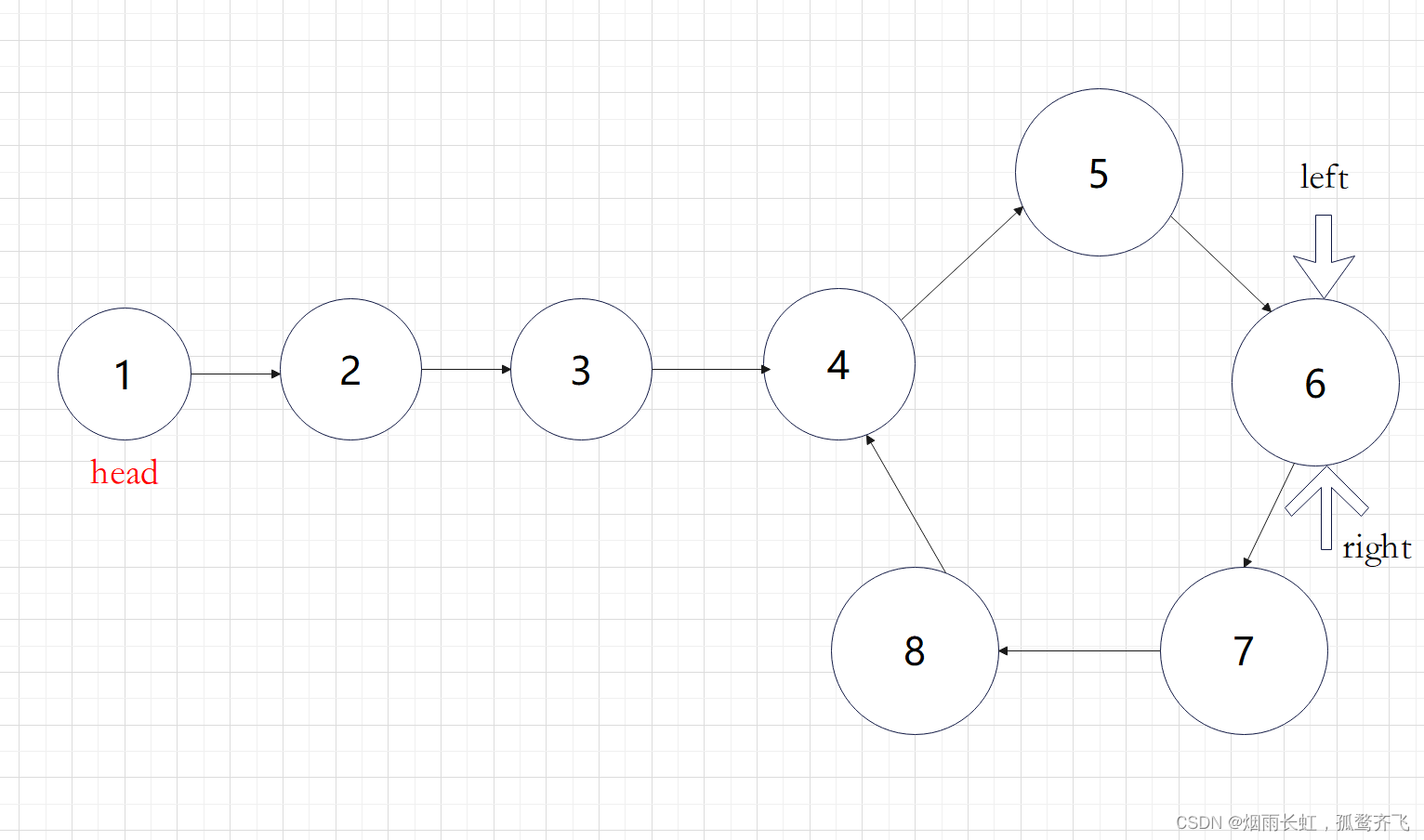
思路我们已经理清楚了，现在的问题是快慢指针的速度为多少才能在圈中相遇呢？

如上图展示：慢指针一次走一步，快指针一次走两步可以在圈中相遇

我们来证明一下：

假设 left 先进环，过一会 right 也进环，这个时候 left 和 right 的距离是N

每追击一次，他们之间的距离就会缩小1步

追击过程中 left 和 right 的距离变化：

N

N-1

N-2

N-2

...

3

2

1

0 相遇

那么快指针一次走3步，走4步，...n步行吗？

如果快指针走三步，慢指针走一步

假设 left 先进环，过一会 right 也进环，这个时候 left 和 right 的距离是N

每追击一次，他们之间的距离就会缩小2步

追击过程中 left 和 right 的距离变化：

N是偶数：

N

N-2

N-4

...

4

2

0 相遇

N是奇数：

N

N-2

N-4

...

3

1

-1 新一轮的追击

-1表示 left 和 right 刚好错过了，但是已经身在环内，所以要展开新一轮的追击

设环的长度为L，他们之间的距离就变成了L-1

如果 L-1 是偶数时，下次追击就可以相遇

但 L-1 仍然是奇数时，left 和 right 就可能永远也不会相遇

如果不是你的那个人，你们可能永远也没有缘分，将要遇见的时候就会错过

分析完毕，我们开始尝试写代码：

代码测试#
class Solution {
public:bool hasCycle(ListNode *head) {ListNode*left = head,*right = head;while(left&&left->next)          //成环判断快慢指针是否相遇，不成环快指针最先为NULL{left = left->next->next;     //快指针走两步right = right->next;         //慢指针走一步if(left == right) return true;}    return false;}
};

环形链表II

题目链接：环形链表II

题目描述#

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
提示：

链表中节点的数目范围在范围 [0, ] 内
<= Node.val <=
pos 的值为 -1 或者链表中的一个有效索引

思路#

快慢指针+数学思维

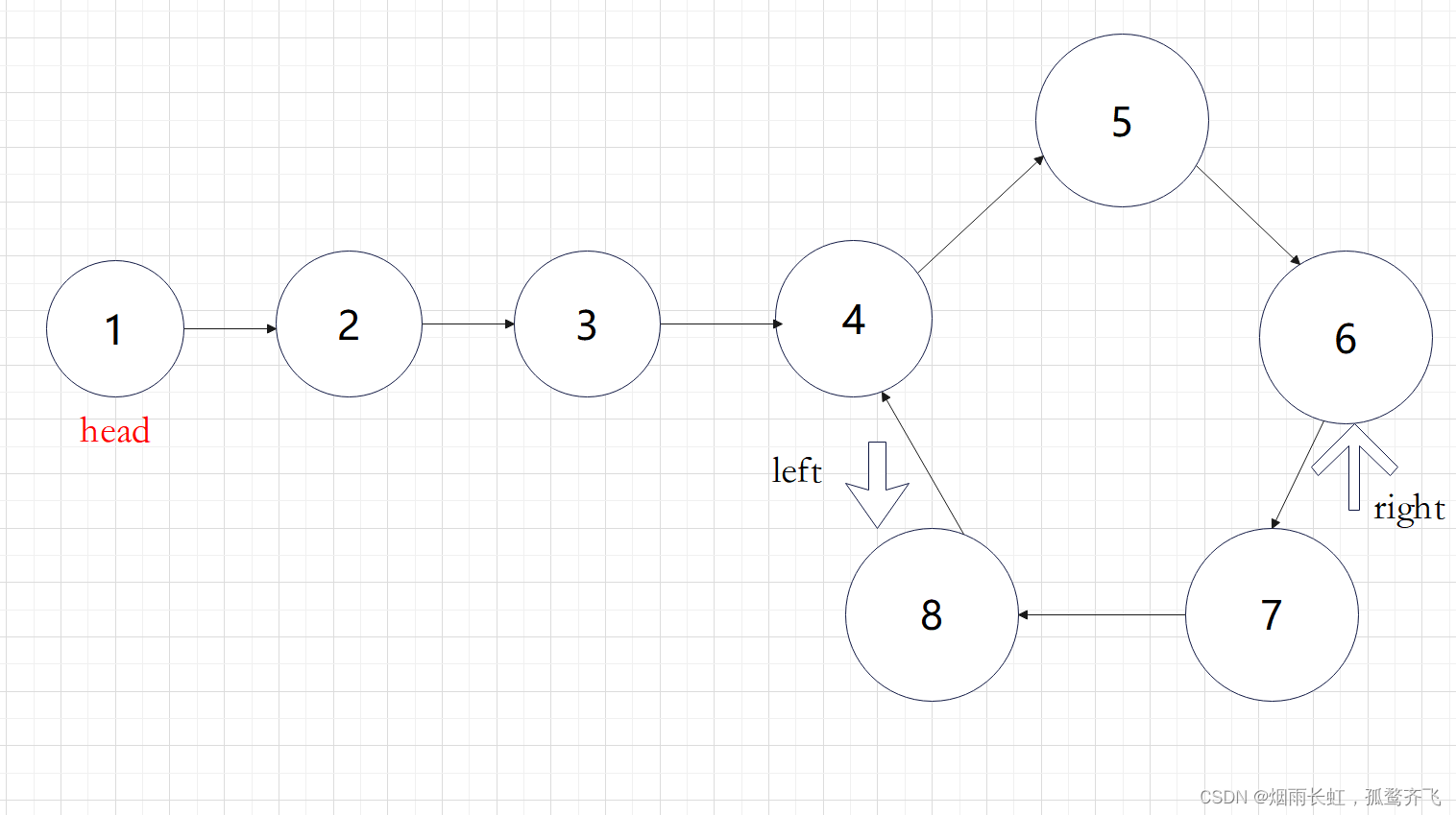
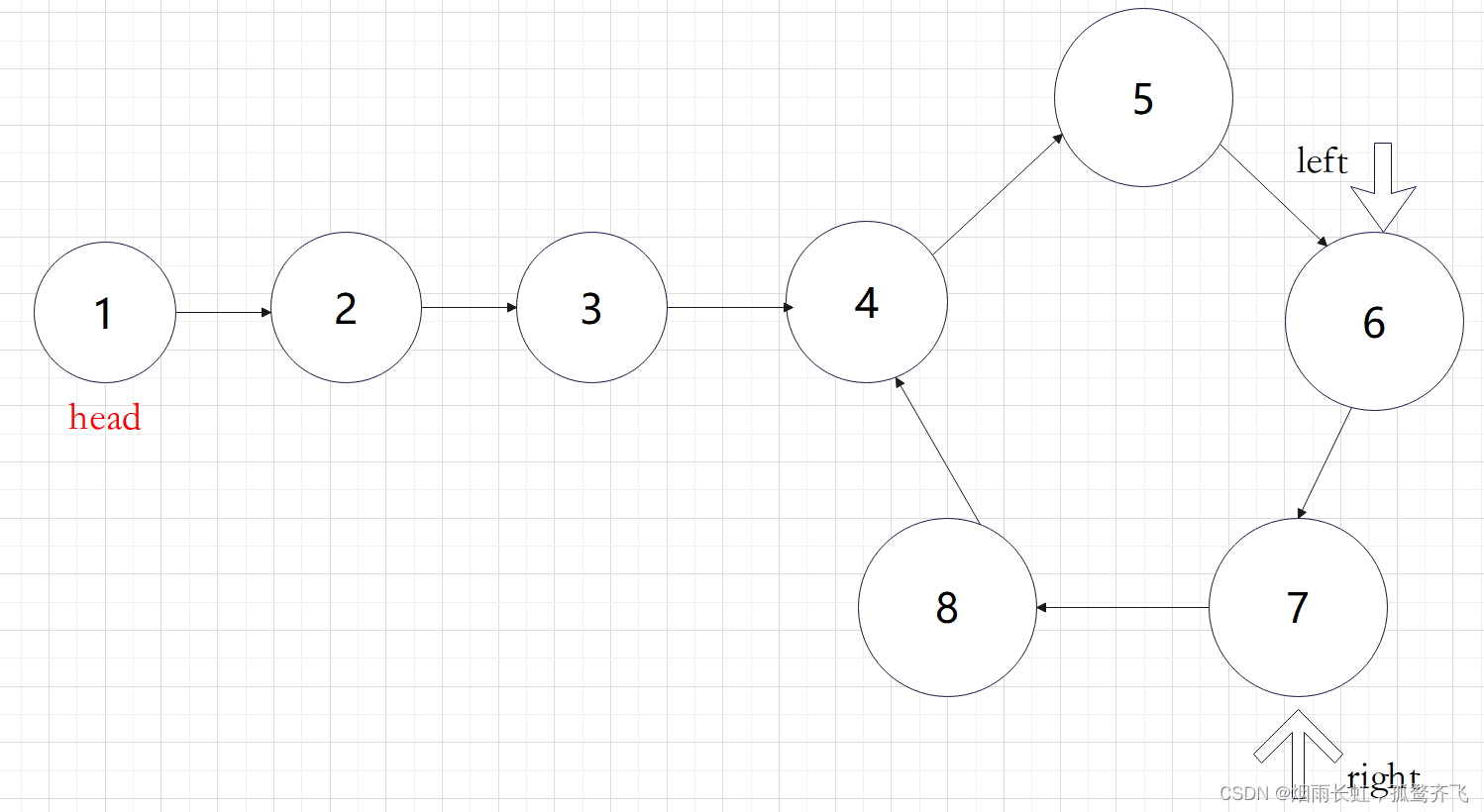
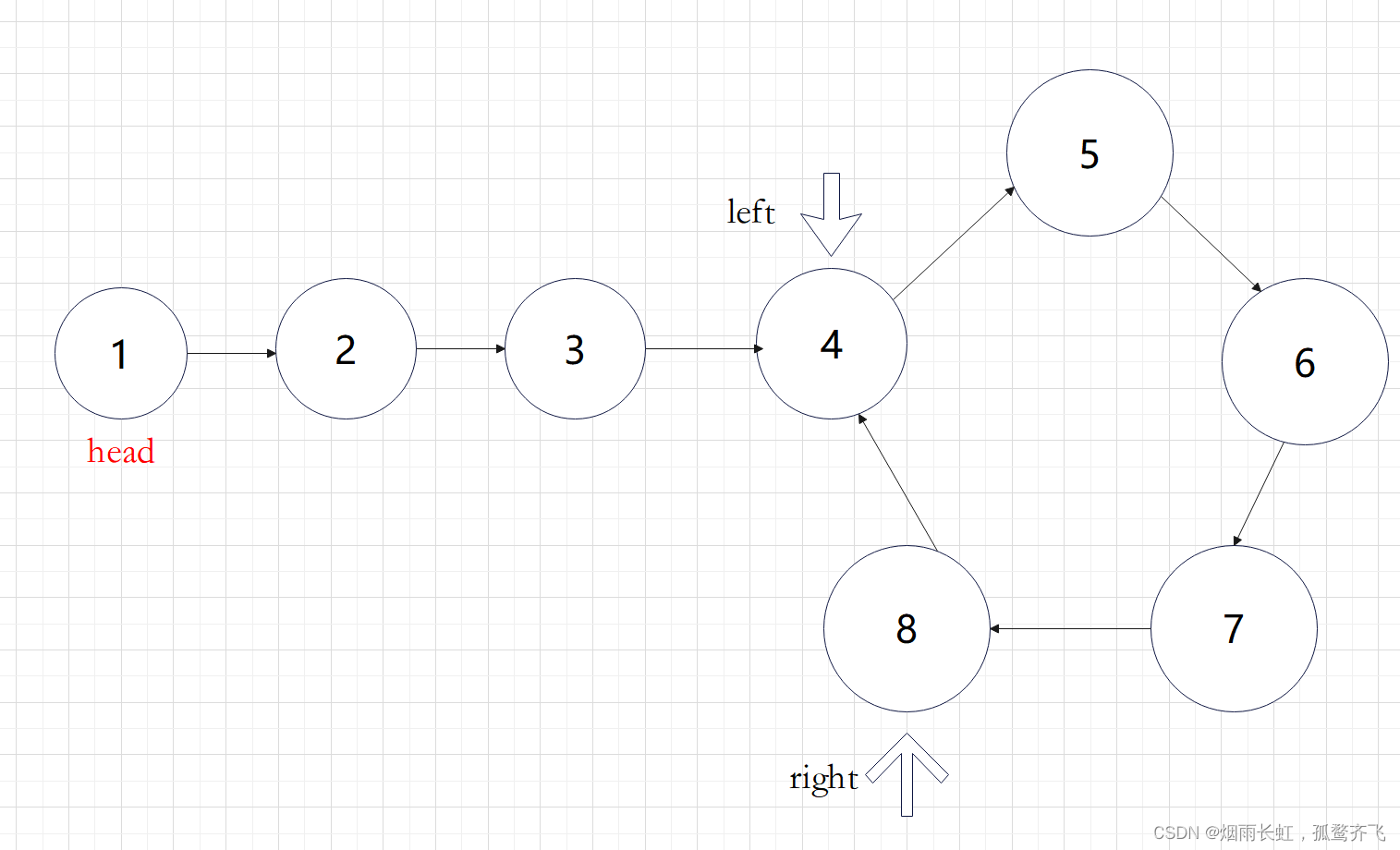
我们承接上一题的结论：先快指针走两步，慢指针走一步找到 相遇点 判断成环

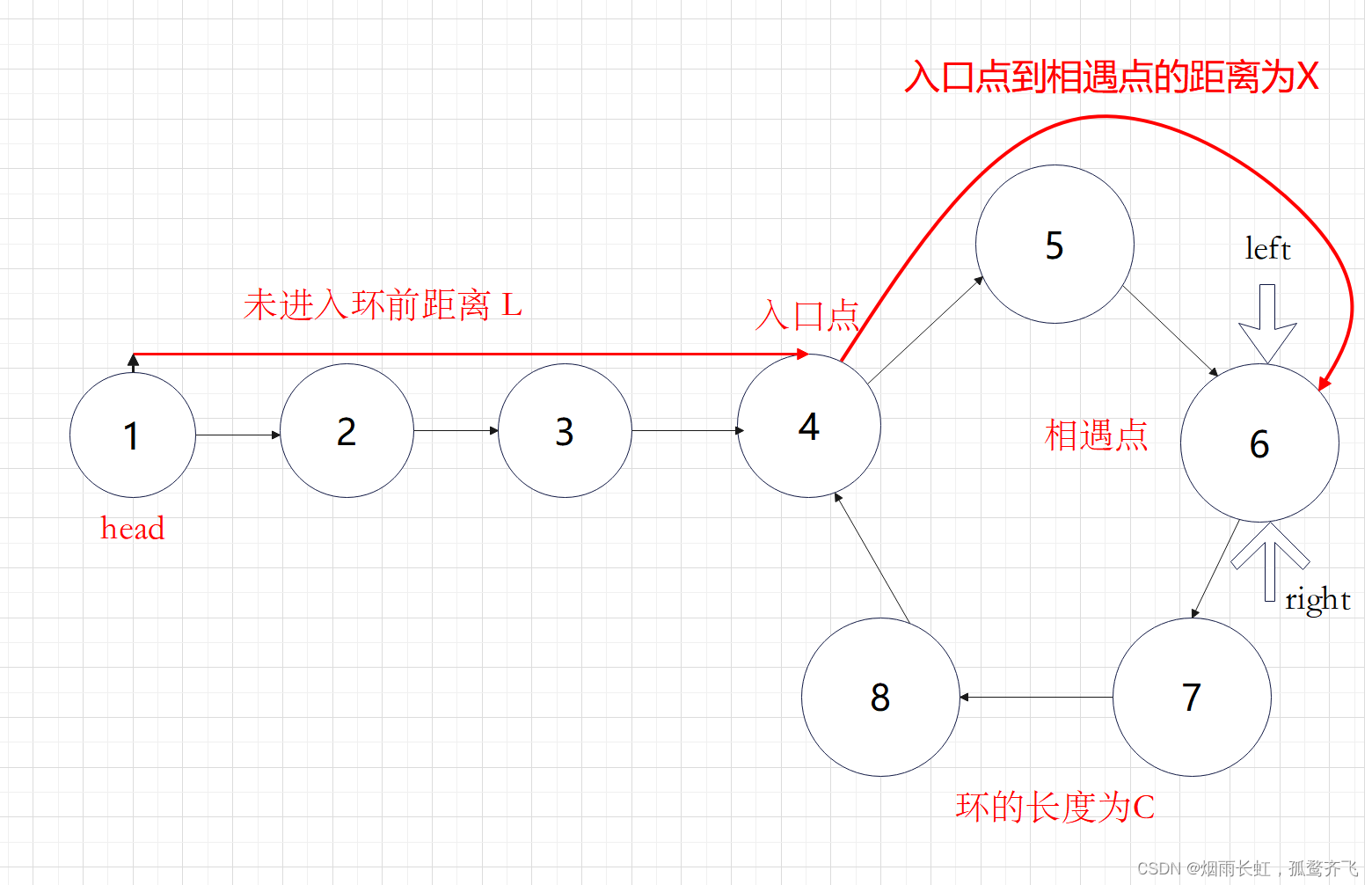
设为进入环前的链表长度为L，入口点到相遇点的距离为X，环的长度为C

追击相遇时：

right 走的距离为 $L+X$

设 left 追上 right 时，转了n圈（n>=1）

left走的距离为 $L+n\times C+X$

任意时刻，left 指针走过的距离都为指针 right 的 2 倍

即为 $2(L+X) = L+n\times C+X$ 化简为： $L= n\times C - X$

为了更好的理解我们写成这样 $L= (n-1)\times C +C- X$

(n-1) x C是 left 转的圈数，转了(n-1)圈后回到相遇点

也就是说：

一个指针在链表头开始走，一个指针在相遇点开始走，他们会在入口点相遇

有些人不用急于寻找，缘分到了自会相遇

分析完毕，我们开始尝试写代码：

代码测试#
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* left = head,*right = head;while(left&&left->next){left = left->next->next;right = right->next;if(left == right){ListNode* mid = left;//相遇点while(mid != head){head = head->next;   mid = mid->next;}return head;         //返回入口位置}}    return NULL;}
};