t检验全析

本文主要是介绍t检验全析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

两个分布

$ch{i}^2$分布

设独立同分布的随机变量$X_1,X_2,...X_n\sim N(0,1)$
令$$X=\sum _{i=1}^n{X}_i^2(1)$$
则称X是自由度为n的${\chi }^2$随机变量。

t分布

设$X\sim N(0,1),Y\sim {\chi }^2(n)$, 且X,Y独立，称：
$$T=\frac{X}{\sqrt{T/n}}(2)$$
为自由度为n的t变量，其分布称为自由度为n的t分布。

三个关键点

设独立同分布的随机变量$X_1,X_2...X_n\sim N(\mu ,{\sigma }^2)$

(3) $\bar{X}\sim N(\mu ,\frac{{\sigma }^2}{n})$

(4) $\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)$

(5) $\bar{X}和S^2独立$

一个重点式子

$$X=\frac{\bar{X}-\mu }{\frac{S}{\sqrt{n}}}\sim t(n-1)(6)$$

由(3)式：
$$\frac{\bar{X}-\mu }{\frac{\sigma }{\sqrt{n}}}\sim N(0,1)(3)$$
由(4)式， 令
$$Y=\frac{(n-1)S^2}{{\sigma }^2}\sim {\chi }^2(n-1)(4)$$
$$\therefore \frac{X}{\sqrt{Y/(n-1)}}\sim t(n-1)(7)$$
代入(3)、(4)式，得:
$$\frac{\frac{\bar{X}-\mu }{\frac{\sigma }{\sqrt{n}}}}{\frac{(n-1)S^2}{{\sigma }^2}/(n-1)}\sim t(n-1)(8)$$
化简得(6)：
$$\frac{\bar{X}-\mu }{\frac{S}{\sqrt{n}}}\sim t(n-1)$$

t-检验

QoG2012.csv 数据集中有一列反映了各个国家的gdp。我们使用这一列数据进行假设检验。
首先要明白的是假设检验是一种反证的方法，也就是

在假定原假设正确的基础上进行推理

原假设($H_0$)： \qquad $\mu =10000$
备择假设($H_1$)： \quad $\mu ̸=10000$

# 导入readr包
library(readr)
library(dplyr)

# 载入data
world_data = read.csv("D://pdf//ucl//day3//day3//QoG2012.csv")

# 对world_data 进行总结
summary(world_data)

# tansform the judiciary to factor
world_data$judiciary <- factor(world_data$judiciary, levels = c(0, 1), labels = c('controled', 'free'))
#transform the former_col to factor
world_data$former_col <- factor(world_data$former_col, levels = c(0, 1), labels = c('no', 'yes'))

# calculate the mean of gdp
gdp_mean = mean(world_data$gdp, na.rm = TRUE)

[1] 10184.09
在这里， gdp_mean就是公式(6)中$\bar{X}$

# calculate se
se <- sd(world_data$gdp, na.rm = TRUE) / sqrt(n)
se

[1] 922.7394
在这里，se就是公式(6)中的$\frac{S}{\sqrt{n}}$

由(6)式：
可以计算得到t.value

t.value <- (gdp_mean - 10000) / se
t.value

[1] 0.1995059

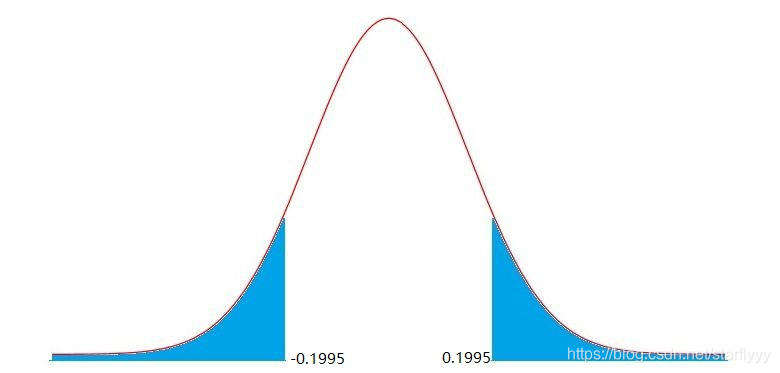
# p-value calculation
2*(1 - pt(t.value, df = (n-1)))

[1] 0.842
pt 函数是t分布的分布函数，df是自由度，由(6)式，符合t(n-1)分布，所以df =n-1
$$pt(t.value,df=n-1)={\int }_{-\infty }^{t.value}{t}_{(n-1)}(x)dx$$
$1-pt(t.value,df=n-1)$ 是右边的尾部，由于是双侧检验，所以
p-value = 2*(1 - pt(t.value, df = n-1))

与三种显著性标准进行比较，发现p-value很大，比0.05的显著性标准还大。
p-value反映的是：
发生比当前情况更加极端情况的概率
可以发现发生比当前情况极端情况的概率是0.842， 也就是说当前情况很容易发生，所以
不能拒绝原假设，也就是说不能够拒绝 $\mu =10000$

后记：
证明(3):
预备知识：
$E(cX)=cE(X)$
$D(cX)=c^{2}D(X)$
由：$$\bar{X}=\frac{\sum _i^n{X}_i}{n}$$
$$E(\bar{X})=E(\frac{\sum _i^n{X}_i}{n})$$

s$$=\frac{1}{n}E(\sum _i^n{X}_i)(9)$$
由于$X_1,X_2...X_n$是独立同分布的正态变量。由期望线性性

所以(9)式可化简为：
$$\frac{1}{n}nE(X)$$
$$=E(X)(10)$$
而$E(X)=\mu$,所以$E(\bar{X})$

$$D(\bar{X})$$
$$=D(\frac{\sum _i^n{X}_i}{n})$$
$$=\frac{1}{n^2}D(\sum _i^n{X}_i)$$
$$=\frac{1}{n^2}nD(X)$$
$$=\frac{1}{n}D(X)$$
即证。

这篇关于t检验全析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---