本文主要是介绍R语言——单因素方差分析笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这学期有一门选修应用统计软件。课上理论讲得不清不楚,编程根本练不着,老师布置的作业就是将他发的代码运行一下写个报告,简直就是机械化的浪费时间的操作。为了不白学这门课,在此稍加整理课上的笔记,供自己以后回顾复习。
一、aov函数
(一)样本服从正态分布
1.代码示例
n1=150; ##n1=50
n2=150; ##n2=50
n3=150; ##n3=50
u1=0.5;
u2=0;
u3=0;
csd=1;
x1=rnorm(n1,u1,csd);
x2=rnorm(n2,u2,csd);
x3=rnorm(n3,u3,csd);
mouse<-data.frame(
X=c(x1,x2,x3),
A=factor(c(rep(1,n1),rep(2,n2), rep(3,n3))))
mouse.aov<-aov(X~A,data=mouse)
source("anova.tab.R"); anova.tab(mouse.aov)
2.部分代码解释
(1)aov()函数提供方差分析表计算,使用方法:aov(formula,data=NULL,projections=FALSE,qr=TRUE,contrasts=NULL,...),结合在线帮助理解。
(2)factor:转换为因子类型,因子在整个计算过程中不作为数值,而是一个”符号”。
3.结果分析


图①是样本量取50的运行结果,P值较大,接受原假设,即三类样本无显著差异;图②是样本量取150的运行结果,P值较小,拒绝原假设,即三类样本存在显著差异。可见样本量越大,检验结果越准确。
(二)样本误差服从T分布(T分布尾部比正态分布重)
1.代码示例
n1=150;
n2=150;
n3=150;
u1=0.5;
u2=0;
u3=0;
df=3 ##自由度为3
x1=u1+rt(n1,df); ##误差生成t分布随机数
x2=u2+rt(n2,df);
x3=u3+rt(n3,df);
mouse<-data.frame(
X=c(x1,x2,x3),
A=factor(c(rep(1,n1),rep(2,n2), rep(3,n3))))
mouse.aov<-aov(X~A, data=mouse)
source("anova.tab.R"); anova.tab(mouse.aov)
2.结果分析

在样本量较大的情况下,所得P值较小,可拒绝原假设。故当样本量较大,误差的分布对于检验的影响较小,而样本均值的差异对于检验影响较大。
二、KW检验
KW检验的优点:对于误差分布无限制,对误差分布无正态性假设。
(一)样本服从正态分布
1.代码示例
n1=50;
n2=50;
n3=50;
u1=0.5;
u2=0;
u3=0;
csd=1;
x1=rnorm(n1,u1,csd);
x2=rnorm(n2,u2,csd);
x3=rnorm(n3,u3,csd);
food<-data.frame(
x=c(x1,x2,x3),
g=factor(rep(1:3, c(n1,n2,n3))))
kruskal.test(x~g, data=food)
2.结果分析

样本量为50时,就能得到在显著性水平取0.05时拒绝原假设的结果。可见KW检验可能比aov函数具有更好的检验效果。
(二)样本误差服从T分布
1.代码示例
n1=200;
n2=200;
n3=200;
u1=0.5;
u2=0;
u3=0;
df=3
x1=u1+rt(n1,df);
x2=u2+rt(n2,df);
x3=u3+rt(n3,df);
food<-data.frame(
x=c(x1,x2,x3),
g=factor(rep(1:3, c(n1,n2,n3))))
kruskal.test(x~g, data=food)
2.代码解释
kruskal.test(formula,data,subset,na.action,...)是K-W秩和检验的函数
3.结果分析

P值很小,故拒绝原假设,即三组样本均值存在显著差异。
三、pairwise检验
(一)样本服从正态分布
1.代码示例
n1=100;
n2=100;
n3=100;
u1=0.5;
u2=0;
u3=0;
csd=1;
x1=rnorm(n1,u1,csd);
x2=rnorm(n2,u2,csd);
x3=rnorm(n3,u3,csd);
X=c(x1,x2,x3)
A=factor(c(rep(1,n1),rep(2,n2), rep(3,n3)))
mu<-c(mean(X[A==1]), mean(X[A==2]), mean(X[A==3])); mu
pairwise.t.test(X, A, p.adjust.method = "none")
pairwise.t.test(X, A, p.adjust.method = "holm")
pairwise.t.test(X, A, p.adjust.method = "bonferroni")
2.代码解释
pairwise.t.test()函数用于均值的多重比较,其使用方法如下:pairwise.t.test(x,g,p.adjust.method=p.adjust.methods,pool.sd=TRUE,...)
其中x是响应向量,g是因子向量,p.adjust.method是P值的调整方法。其中,调整方法由p.adjust()给出,详见p.adjust()函数的在线帮助。若p.adjust.method = "none",表示不做任何调整;缺省值按“holm”作调整。
3.结果分析

首先由均值的估计可见,μ1与μ2、μ3存在较大差异。利用三种pairwise的检验方法,均得到μ1与μ2、μ3的检验P值低于显著性水平0.05,故μ1与μ2、μ3存在显著差异;而μ2与μ3之间检验P值较大,故接受原假设,即μ2与μ3之间无显著差异。
(二)样本误差服从自由度为3的T分布
1.代码示例
n1=200;
n2=200;
n3=200;
u1=0.5;
u2=0;
u3=0;
df=3
x1=u1+rt(n1,df);
x2=u2+rt(n2,df);
x3=u3+rt(n3,df);
X=c(x1,x2,x3)
A=factor(c(rep(1,n1),rep(2,n2), rep(3,n3)))
mu<-c(mean(X[A==1]), mean(X[A==2]), mean(X[A==3])); mu
pairwise.t.test(X, A, p.adjust.method = "none")
pairwise.t.test(X, A, p.adjust.method = "holm")
pairwise.t.test(X, A, p.adjust.method = "bonferroni")
2.结果分析

分析结果同上。
PS:有时运行结果会出现错误,得到不准确的检验结果。多运行几次,能够避免取错误的检验结果。
四、Bartlett检验
1.代码示例
n1=50;
n2=50;
n3=50;
n4=50;
lamp<-data.frame(
X=c(rnorm(n1,0,1),rnorm(n2,0,2),rnorm(n3,0,2),rnorm(n4,0,2)),
A=factor(c(rep(1,n1),rep(2,n2), rep(3,n3), rep(4,n4))))
bartlett.test(X~A, data=lamp)
bartlett.test(lamp$X, lamp$A) ##bartlett.test函数的另一种使用方法
2.代码解释
bartlett.test()函数用于方差齐性检验,其使用格式为bartlett.test(x,g,..),其中x是由数据构成的向量或列表,g是由因子构成的向量,x是列表时,此项无效;或使用另一种格式bartlett.test(formula,data,subset,na.action,...),可借助在线帮助理解各参数含义。
3.结果分析

所得P值很小,故拒绝原假设,即样本间的方差存在显著差异。符合样本的设定。
五、friedman检验
friedman检验用于多个样本的比较,如果它们的总体不能满足正态性和方差齐性的要求。firedman检验原假设为:各方法处理效果无显著差异。
1.代码示例
##各变量之间有相关性##
n=1000
p=3;
alpha=0.5;
sig=1;
##均值
mu=c(0.5,rep(0,p-1));
##协方差矩阵
Sm=sig*toeplitz(c(1,rep(alpha, p-1)));
Sm
#Sm=sig*toeplitz(alpha^(c(0:(p-1))));
#Sm
ev<-eigen(Sm);
lam=ev$values;
vec=ev$vectors;
Sr=vec%*%sqrt(diag(lam))%*%t(vec)
#Sm-Sr%*%Sr;
x=t(t(matrix(rnorm(n*p),ncol=p)%*%Sr)+mu);
apply(x,2,mean)
var(x)
friedman.test(x)
2.代码解释
friedman检验的函数为friedman.test(y,groups,blocks,...),或者friedman.test(formula,data,subset,na.action,...)
3.结果分析
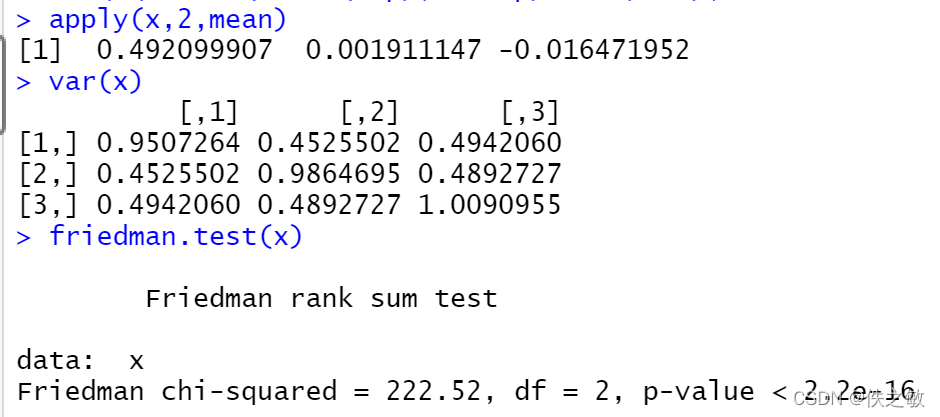
由均值的估计得出,μ1与μ2、μ3存在较大差异。协方差阵显示出不同样本之间存在较大的相关性。Friedman检验的P值非常小,故拒绝原假设,即样本之间存在显著差异。
这篇关于R语言——单因素方差分析笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



