如何在Python中绘制置信区间？

本文主要是介绍如何在Python中绘制置信区间？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

置信区间是从观测数据的统计量计算的一种估计值，它给出了一个可能包含具有特定置信水平的总体参数的值范围。

平均值的置信区间是总体平均值可能位于其间的值的范围。如果我预测明天的天气在零下100度到+100度之间，我可以100%肯定这是正确的。然而，如果我预测温度在20.4到20.5摄氏度之间，我就不那么有信心了。注意置信度如何随着区间的减小而减小。这同样适用于统计置信区间，但它们也依赖于其他因素。

一个95%的置信区间，会告诉我，如果我们从我的总体中取无限多个样本，每次计算区间，那么在95%的区间中，区间将包含真正的总体均值。因此，对于一个样本，我们可以计算样本均值，并从中得到一个区间，该区间最有可能包含真实的总体均值。

在这里插入图片描述
置信区间（Confidence Interval）的概念是由Jerzy Neyman在1937年发表的一篇论文中提出的。置信区间有多种类型，最常用的是：平均值CI，中位数CI，平均值差异CI，比例CI和比例差异CI。

使用linepot()计算给定底层分布的CI

Seaborn中提供的lineplot（）函数是一个Python数据可视化库，它最适合显示一段时间内的趋势，但它也有助于绘制置信区间。

sns.lineplot(x=None, y=None, hue=None, size=None, style=None, data=None, palette=None, hue_order=None, hue_norm=None, sizes=None, size_order=None, size_norm=None, dashes=True, markers=None, style_order=None, units=None, estimator=’mean’, ci=95, n_boot=1000, sort=True, err_style=’band’, err_kws=None, legend=’brief’, ax=None, **kwargs,)

默认情况下，该图在每个x值处聚合多个y值，并显示集中趋势的估计值和该估计值的置信区间。

示例

# import libraries 
import numpy as np 
import seaborn as sns 
import matplotlib.pyplot as plt # generate random data 
np.random.seed(0) 
x = np.random.randint(0, 30, 100) 
y = x+np.random.normal(0, 1, 100) # create lineplot 
ax = sns.lineplot(x, y)

在上面的代码中，变量x将存储从0（含）到30（不含）的100个随机整数，变量y将存储来自高斯（正态）分布的100个样本，该分布以0为中心，扩展/标准偏差为1。NumPy操作通常在逐个元素的基础上对数组对进行。在最简单的情况下，两个数组必须具有完全相同的形状，如上面的示例所示。最后，在seaborn库的帮助下创建一个默认为95%置信区间的线图。置信区间可以很容易地通过改变位于[0，100]范围内的参数“ci”的值来改变，这里我没有传递这个参数，因此它认为默认值为95。

在这里插入图片描述
浅蓝色阴影表示该点周围的置信水平，如果置信度较高，则阴影线将更粗。

使用regplot（）计算给定底层分布CI

seaborn.regplot（）帮助绘制数据和线性回归模型拟合。此功能还允许绘制置信区间。

seaborn.regplot( x, y, data=None, x_estimator=None, x_bins=None, x_ci=’ci’, scatter=True, fit_reg=True, ci=95, n_boot=1000, units=None, order=1, logistic=False, lowess=False, robust=False, logx=False, x_partial=None, y_partial=None, truncate=False, dropna=True, x_jitter=None, y_jitter=None, label=None, color=None, marker=’o’, scatter_kws=None, line_kws=None, ax=None)

基本上，它包括散点图中的回归线，并有助于查看两个变量之间的任何线性关系。下面的例子将展示如何使用它来绘制置信区间。

# import libraries 
import numpy as np 
import seaborn as sns 
import matplotlib.pyplot as plt # create random data 
np.random.seed(0) 
x = np.random.randint(0, 10, 10) 
y = x+np.random.normal(0, 1, 10) # create regression plot 
ax = sns.regplot(x, y, ci=80)

regplot（）函数的工作方式与lineplot（）相同，默认情况下置信区间为95%。置信区间可以通过改变位于[0，100]范围内的参数“ci”的值来容易地改变。这里我传递了ci=80，这意味着绘制的置信区间不是默认的95%，而是80%。

在这里插入图片描述
淡蓝色阴影的宽度表示回归线周围的置信水平。

使用Bootstrapping计算CI

Bootstrapping是一种使用随机抽样和替换的测试/度量。它给出了准确性的度量（偏差、方差、置信区间、预测误差等）抽样估计。它允许使用随机抽样方法估计大多数统计量的抽样分布。它也可以用于构建假设检验。

# import libraries 
import pandas 
import numpy 
from sklearn.utils import resample 
from sklearn.metrics import accuracy_score 
from matplotlib import pyplot as plt # load dataset 
x = numpy.array([180,162,158,172,168,150,171,183,165,176]) # configure bootstrap 
n_iterations = 1000 # here k=no. of bootstrapped samples 
n_size = int(len(x)) # run bootstrap 
medians = list() 
for i in range(n_iterations): s = resample(x, n_samples=n_size); m = numpy.median(s); medians.append(m) # plot scores 
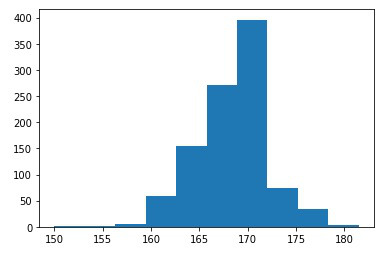
plt.hist(medians) 
plt.show() # confidence intervals 
alpha = 0.95
p = ((1.0-alpha)/2.0) * 100
lower = numpy.percentile(medians, p) 
p = (alpha+((1.0-alpha)/2.0)) * 100
upper = numpy.percentile(medians, p) print(f"\n{alpha*100} confidence interval {lower} and {upper}")

导入所有必要的库后，创建一个大小为n=10的样本S，并将其存储在变量x中。使用简单的循环生成1000个样本（=k），每个样本大小m=10（因为m<=n）。这些样本称为bootstrapped样本。计算它们的中位数并将其存储在列表“medians”中。借助matplotlib库绘制1000个bootstrapped样本的中位数直方图，并使用样本统计量的公式置信区间计算基于样本数据计算的指定置信水平下统计量总体值的上限和下限。

在这里插入图片描述