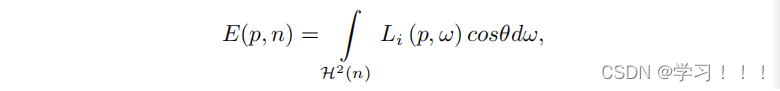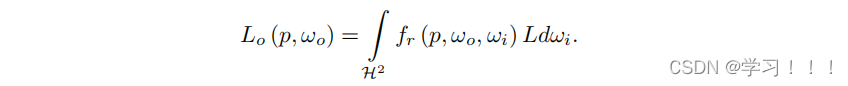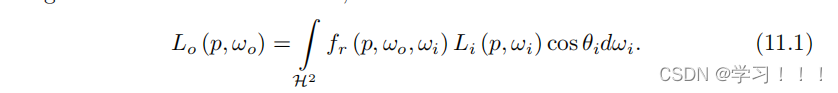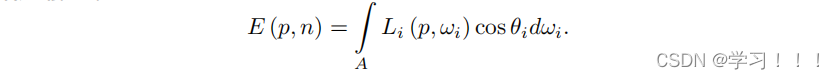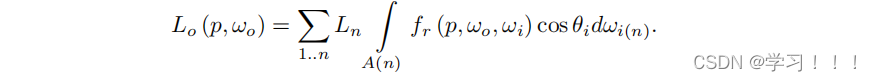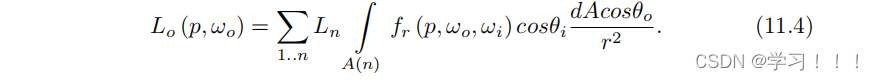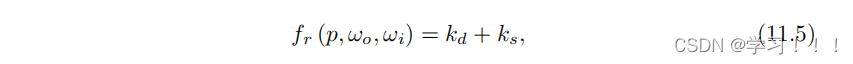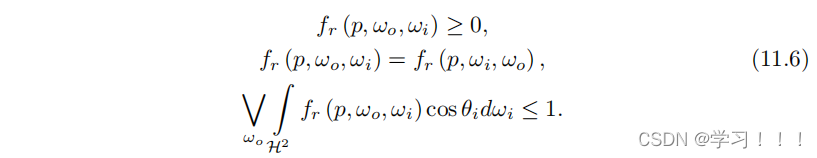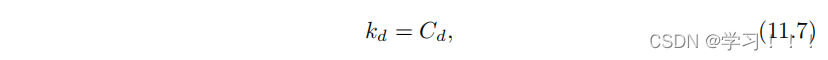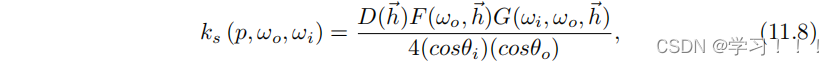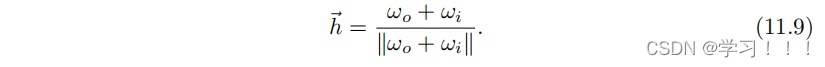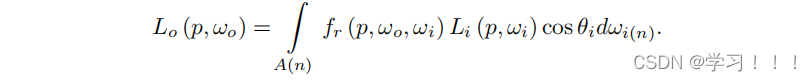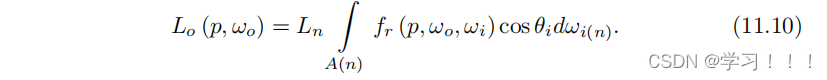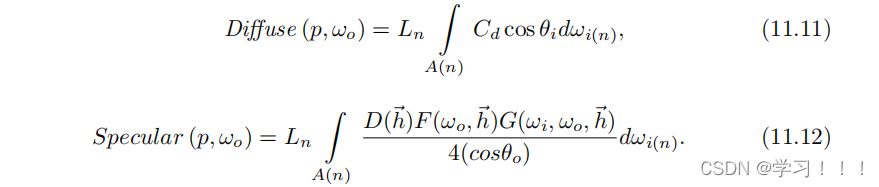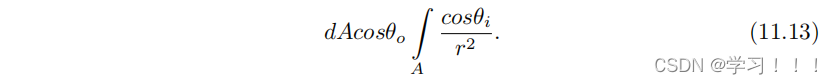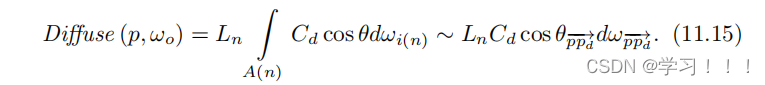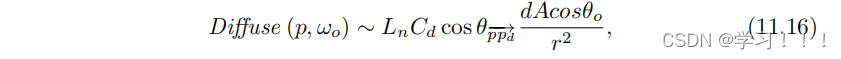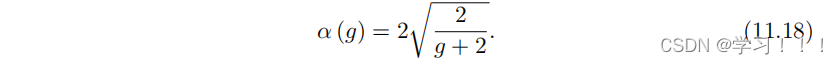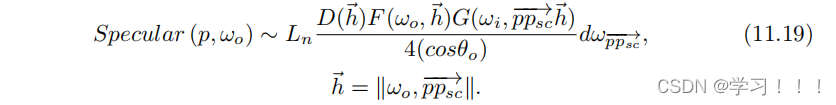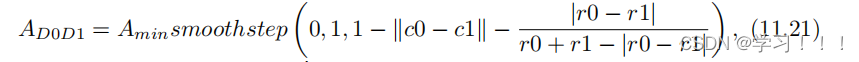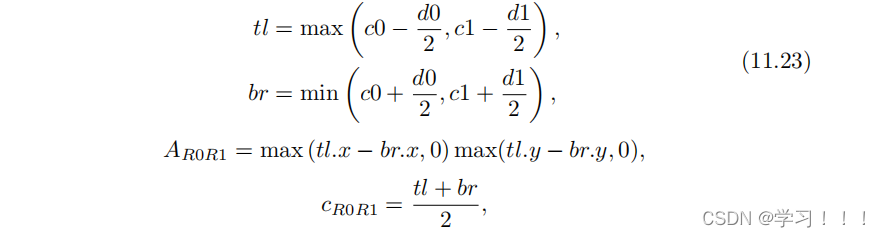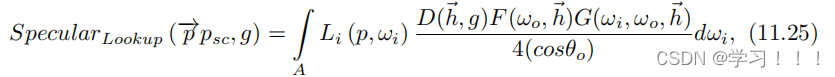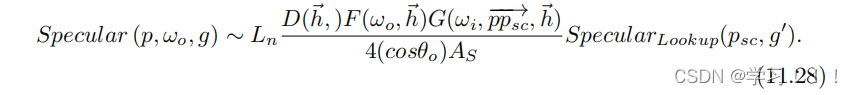Physically Based Area Lights

所有在渲染引擎中的光源都是基于物理的面光源，由辐射度量值描述，例如流明的光强度、米的尺寸、世界方向和光源形状类型。我们引入了一种专门的表面粗糙度描述，该描述可以共享或调整以匹配各种表面反射模型。光模型利用光源描述和表面粗糙度，在正在着色的点上，传递到该点的光数量分为光模型和表面反射模型。

此外，我们讨论了将所提出的模型集成到延迟渲染器中的方法，以及它如何被用作环境探针生成和基于动态分析纹理的面光源的原则。

11.2 简介

目前，游戏行业标准的光照模型是基于Blinn-Phong BRDF或直接基于它的模型。近年来，我们看到了多项进展，扩展了该模型以支持更多样的材料、表面特性和基于物理的属性[McAuley et al. 13]，或者采用解决混叠问题的方法[Baker and Hill 12]。这项技术推动的结果是广泛获得了一种高效、可预测、广为人知的光照模型，能够捕捉我们在常见情景中可能观察到的大多数材料特性。大多数研究侧重于优化材料相互作用，包括在Cook-Torrance光照模型中提出的著名几何和菲涅尔项[Cook and Torrance 81]。然而，该模型仍然存在一个非常基本的限制，即它只能模拟基于点光源的情况。在几乎所有情景中，光源都具有物理大小，这在现实生活中通过镜面反射和漫反射光照响应的正确形状来体现。在许多情况下，使用 Blinn-Phong 点光源来处理动态光源都是不足够的，导致场景中可见光源和光照结果之间存在视觉分离（见图11.2和11.3）。

有几种方法可以解决这个问题。其中一些方法包括预先计算 "light cards" 或广告牌反射，并在运行时使用光线追踪来模拟准确的镜面反射[Mittring and Dudash 11]。不幸的是，这个系统是在标准的解析动态点光照的基础上进行的补充。此外，它并没有提供面积基础的漫反射照明的解决方案。

解决这个问题的另一种方法是采用基于全局光照的解决方案。已经有几个商业引擎实现了这种系统，主要是基于体素的[Mittring 12]。然而，由于稳定性、分辨率或质量差异，它们无法完全替代解析光源。

在我们对下一代平台的 Killzone 引擎进行新迭代的研究过程中，我们希望利用当前对光照模型的了解，并将其扩展到非点光源。统一处理艺术制作也是我们的首要任务。随着我们过渡到基于物理的材质建模，我们还希望使用基于物理的光源，使用真实世界的辐射度量单位，从而实现可预测的着色模型。

我们决定利用现有的BRDF（双向反射分布函数）来模拟表面对光的反应，并重新设计提供给这些模型的照明信息的方式。标准的BRDF假设光只从一个方向进入，强度以每个光源的设定数量给出。当处理面积光源时，我们需要解决对整个光源形状上所有点的照明模型的积分。这可以通过数值方法实现，但不幸的是，在实时应用中，这在性能上是不可行的。然而，该积分的一部分可以通过辐射度积分进行解析计算，而其余部分可以进行高效的近似计算。

11.3 区域照明模型

11.3.1 辐射积分和 BRDF 定义

在本节中，我们介绍了基本的辐射度量单位，如光强度、辐照度和辐射度[Pharr和Humphreys 04]。然后，我们定义了解决区域照明模型所必需的辐射积分。
    让强度被定义为单位立体角的光通量密度：
                            

其中dϕ是光通量微分，dω是固体角微分。强度仅对点光源有意义。
    辐照度定义了单位面积上的总光通量：
                                                                                        E = dΦ / dA 
其中dA是接收光通量的微分面积。
        Radiance描述了单位面积、单位立体角的光通量密度。
                                                                                        L = dΦ / dw dA⊥
其中dA⊥是dA在与固体角垂直的假设表面上的投影面积。

我们还将辐射度发射Lo(p, ω)和进入表面上一点的入射辐射度Li(p, ω)定义为点和方向的函数。
    辐照度在点p上，其法向量为n，可以定义为：

        

其中，cosθ dω是投影的立体角dω⊥，其中θ是ω和表面法线n之间的角度。这个术语来自辐射度的定义。换句话说，这个方程式对半球上所有方向的入射光进行积分，围绕一个给定法线的积分点，关于投影的立体角。

双向反射分布函数（BRDF）定义了从表面点向观察者方向反射的光的比例，以及从特定方向进入表面的光的量。因此，BRDF 的基本定义是这样的：
                                                                         fr(p, wo, wi) = dLo(p, wo) / dE(p, wi) .

在实时图形中，我们希望找到关于点 p 和表面法线向量 n 周围整个半球 H 的积分 Lo(p, ωo)。因此，我们要寻找的是：
 

使用辐射度L的定义，
 

在渲染过程中，我们评估了有限数量的光源。因此，我们对表面积上的积分表示感兴趣。在辐照度覆盖A的情况下，我们可以定义为：
 

在简化情况下的n个贡献光源，我们可以将方程（11.1）表示为从点p可见的所有面光源的积分之和:
 

方程（11.2）是我们所有推到的基础照明方程。
    为简化起见，我们可以假设光源具有均匀的光通量分布，因此L(p, w)是常数表示为L，因此，
 

微分立体角也与微分面积相关、
    在定义在四边形光源的相关情况下，微分立体角可以表示为关于光的微分面积的函数:
    

其中 r 是从表面点 p 到dA上的 p' 的距离，θo 是在表面dA 上的 p'点的法线和p'p的之间夹角。
    值得注意的是，固体角对于多个可以用作光源形状的基元是明确定义的，如圆盘和矩形。
最后，每个单独光源的辐射度被定义为
 

11.3.2 材质和光照模型
        在推导光渲染的主要积分（方程（11.4））之后，我们假设光区域被明确定义，并因此可以进行积分。为了简化问题，我们将推理限制在简单的形状上，例如球体、圆盘和矩形，这些形状相对容易积分和计算。
        我们的光源由以下参数定义：
其中 kd 是漫反射光模型，ks 是镜面模型。
        我们还需要设定其他要求，使得这个 BRDF 是基于物理的：
 

对于我们的 kd，我们可以使用标准的兰伯特漫反射模型[Lambert 60]。当作为 fr (p, ωo, ωi) 的一部分时，它采取非常简单的形式：
 

其中Cd被定义为表面漫反射颜色。
        我们选择广义的 Cook-Torrance BRDF [Cook and Torrance 81] 作为我们微表面镜面模型的基础：
 

其中 D(h) 是围绕表面法线 n'' 的微表面分布，F(ωo,h) 是菲涅尔反射函数，G(ωi, ωo, h) 是几何函数。如前所述，θi 是 n 和 ωi 之间的角度，θo 是 n 和 ωo 之间的角度。一般来说，h 被称为半向量，定义为
 

我们感兴趣的是找到以查看者方向为中心的辐射度，每个光源，描述如下：
 

目前，我们可以假设，就像方程（11.2）中一样，Li(p, ωi) 在光源上是常数：
 

现在用方程（11.10）的部分，替换为方程（11.5），（11.7）和（11.8）：
 

要得到镜面积分的最终形式，我们需要选择函数 DFG。有多种来源可供讨论针对特定使用情景的最佳选择[Burley 12]。
 

 不幸的是，无论选择的函数如何，方程（11.11）和（11.12）中的积分对于球体以外的形状来说都不容易求解。因此，我们将专注于为可以用四边形上的二维函数表示的光源形状找到适当的近似方法。

11.3.3 近似漫反射积分
 蒙特卡洛方法和重要性抽样。
        解决积分的一种已知方式是通过离散部分的数值积分。有多种方法和技术可以加速这个过程。对我们来说，特别有趣的一种技术是蒙特卡洛技术，一般可以描述如下步骤：         通过给定概率分布，期望方差和最小可接受误差的估计器也是已知的。使用重要性抽样技术[Pharr and Humphreys 04]可以大大加快这个过程。
        重要性抽样的原理是优先选择对最终结果影响最大的样本。我们可以使用空间启发式来找到这样的样本。另一种解决方案是使用较少数量的样本运行蒙特卡洛积分的初始步骤，以估计结果的方差，从而决定哪些积分区域将使用更重要的样本。
        重要性抽样是一个正在积极研究的主题，有多种不同的解决方案。我们的推理结论是，在任何积分中，有些样本比其他样本更重要，因此可以在给定数量的样本下最小化误差估计器。
应用于漫反射积分。
        我们希望将蒙特卡洛方法应用于我们的漫反射积分。为了简化这个过程，我们假设光源形状具有均匀的表面法线 n。另一个假设是积分点的 dA 不会改变，这意味着整个形状始终可见。因此，我们可以概念上将 dA cosθo 移出我们的积分，并为整个域计算一次：
 

综合函数仅依赖于距离和表面法线与光源形状所围成的方向之间的余弦。这些是连续且明确定义的函数。
        我们立即可以看到集成函数的全局最小值和最大值位于由光源形状定义的采样域内。因此，存在一个单一点，在光源形状上能够代表积分，从而最小化误差估计器。
      
        我们感兴趣的函数在光形状的边界内被限定，并且定义为
 

我们知道，函数在给定区域的积分被局部极小值和极大值所限定。方程（11.14）中的函数在形状边界上具有一个全局最小值和一个全局最大值。因此，我们知道可以在最大值和最小值之间的一段区间内找到最佳代表积分的单个点。为了找到这个点，我们需要计算全局最小值和最大值，但我们认为这样做的计算量太大。

相反，我们决定在全局最大值附近找到一个近似的重要点，接受过高估计的风险。为了做到这一点，我们需要为我们的搜索设置边界条件。方程（11.14）的函数是两个函数的逐分量乘积。它们的乘积的最大值可以在连接它们的局部最大值的线段上找到。
 

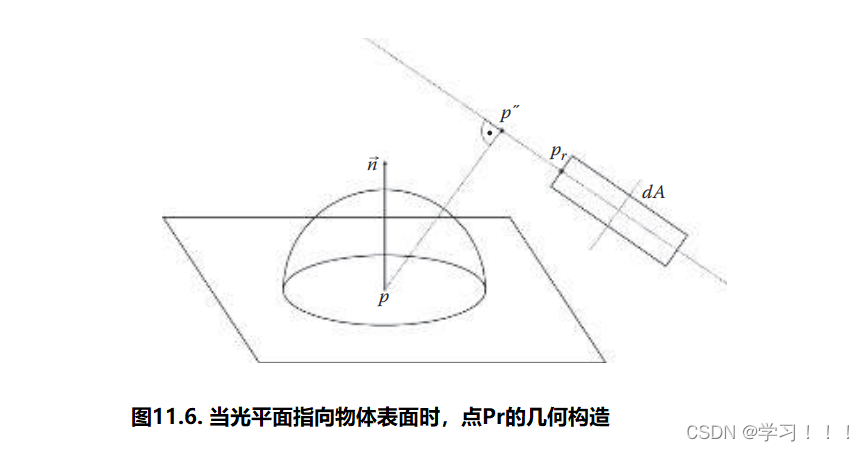
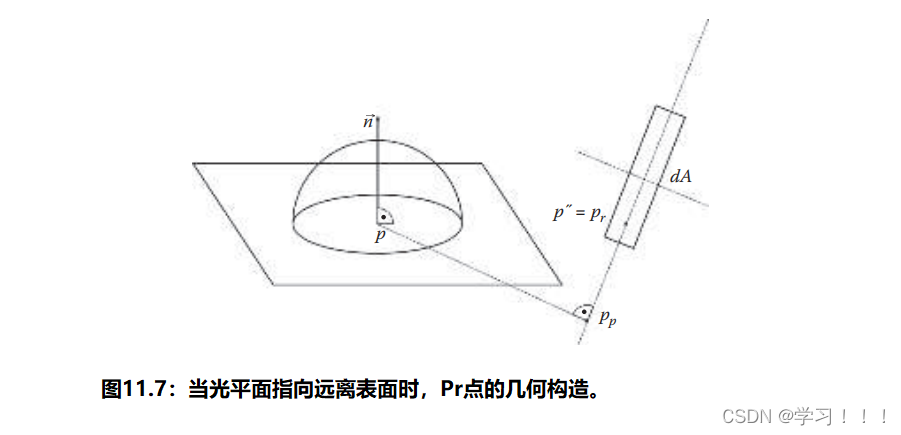
我们可以通过从点p沿着表面法线n的方向投射一条射线，创建点p′，与光平面相交，并找到与p′最接近的形状上的位置，称为pc（见图11.5），轻松地找到cosθo的最大值。值得注意的是，在光平面指向远离表面法线的情况下（即n·n′ > 0），向量pp′应该向光平面的方向倾斜，以获得相交点（见图11.5）。

可以通过将点p投影到光平面上，创建点pp，找到正半球上与pp最接近的点，称为p′′，最后找到与pr最接近的光形状上的点，找到1 / r*r的最大值（见图11.6和11.7）。

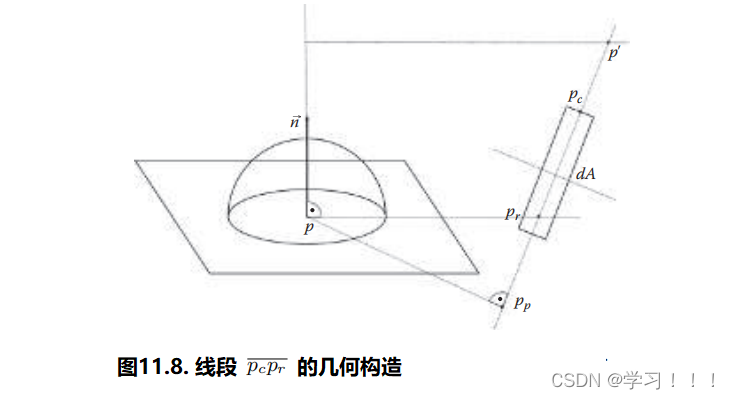
正如之前讨论的，我们正在寻找在pr和pc之间的线段上代表逐分量(component-wise) 局部最大值的最重要的积分样本（见图11.8）

在设置了这些条件之后，我们使用计算软件包在pc pr线上 数值地找到尽可能接近最重要点的点。我们处理了一个生成为圆盘或矩形光形状的几百个区域光的数据集。对于每个光形状，我们找到了在平面上最接近完整积分的点。然后，我们计算了pc和pr之间线段的端点（就像它将在运行时计算一样）。然后，我们在线段上数值地检查点，计算光照方程并与参考值进行比较，使用最小二乘法找到最准确代表积分的点pd。

            

              

        在评估了许多测试案例和各种复杂度的函数之后，我们注意到，将 ppc 和 ppr 的中间向量与光平面相交，创建pd（见图11.9），在我们的大部分情况下效果还不错，与最佳点近似积分的结果的统计误差小于0.05。
        经过目测评估，我们认为这种方法在我们的应用案例中效果足够好（见图 11.10），而且在视觉上与光线步进解法相差不大（见图 11.11）。事实证明，在现代 GPU 上进行每像素实时计算也足够简单。

       作为另一种简化，我们使用了 pp′ 和 pp′′ 之间的中间矢量。它可以跳过与形状计算最接近的点，从而实现重要的优化。遗憾的是，它产生了一个大于0.15的统计误差。然而，在大多数情况下，这种差异主要在边缘情况下可见，即光线形状偏离表面法线。没有明显的视觉伪影，我们的美工人员认为这足以满足我们的需求。
 

空间漫反射近似算法。
       因此，我们最终的漫反射积分近似算法可以用下面的伪代码表示：
- 对于法线为 n 的点 p：     ◦ 将矢量 ppd 视为漫射方程中的光矢量，有效逼近方程 (11.11) 中的漫射积分：
        
    

        在公式 (11.15) 中，我们假设 Ln 在整个光照区域内都是恒定的。新的光矢量 ppd 与表面法线 n 之间的夹角为 θ ppd.
 

        我们还可以用公式 (11.3) 将微分实体角表示为距离和微分面积的函数。因此，我们最终的近似漫反射积分为
 

       
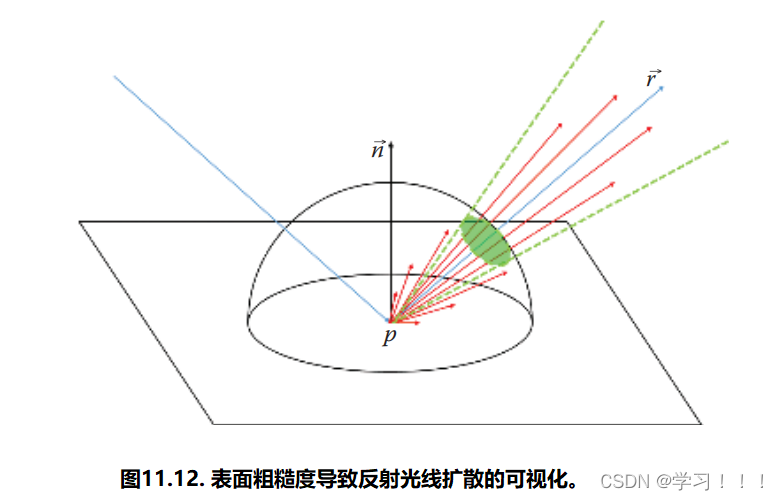
其中，θo 是表面法线 n 与光平面方向法线 nl 之间的夹角，dA 由光形状给出。         重要采样中的镜面反射: 如果我们使用蒙特卡洛方法来渲染镜面反射，我们会在正在着色的点周围的每个方向上投射一条光线，并评估给定函数DFG（来自公式11.12）的镜面BRDF。此外，用于建模D的每个PDF都取决于某种表面粗糙度参数g。该参数描述了光线在反射表面上反射后的聚焦程度。
        在镜面反射的情况下，我们可以定义一个由反射在观察者方向ωo上与表面法线n相对的向量r。这样的向量被称为反射向量。
        由于镜面反射的性质，大多数具有有意义权重的样本会在 r 附近聚集。它们在最终解决方案上的权重将直接与被积分到 r 的射线的角距离相关。它们还直接与材料参数g相关。因此，我们可以定义一种重要性采样的镜面锥体，以r为中心，包含所有重要的射线样本（见图11.12）。
 

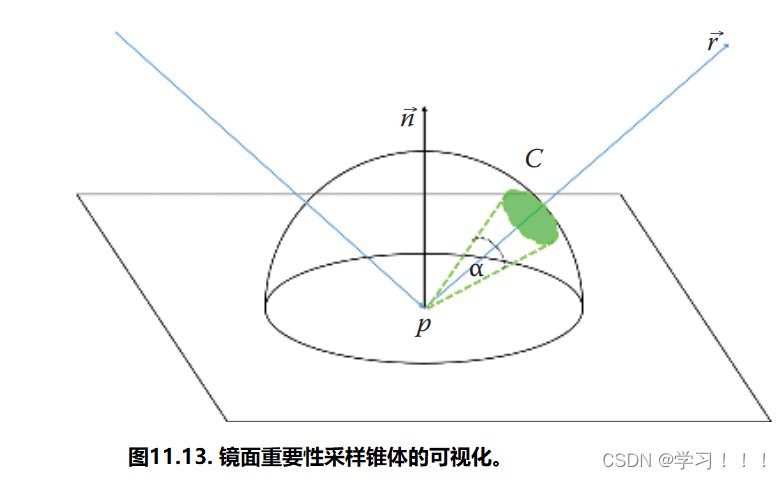
        通过重要一词，我们指的是每条射线的绝对权重大于阈值σ（假设以 r 方向发射的射线的权重为1.0）。我们可以很容易地看出，对于恒定的σ，锥体的顶角α仅取决于表面光泽因子g（见图11.13）。因此，我们希望找到一个从表面光泽计算镜面锥体角度的函数，该函数具有给定的镜面模型和常数σ。

以Phong镜面模型为例，我们可以应用这种推理来找到这样一个函数:
 

        我们准备了包含在 α 处 Kphong > σ 的镜面锥角α的数据。然后，对于给定的数据集，我们找到一个近似函数。从可能的候选函数中选择计算成本最低的函数。在我们的情况下，我们选择了以下函数:
 

它与粗糙度m的 Beckmann 分布定义完全一致[Beckmann and Spizzichino 63]，其中m设置为镜面锥斜率的均方根。
 

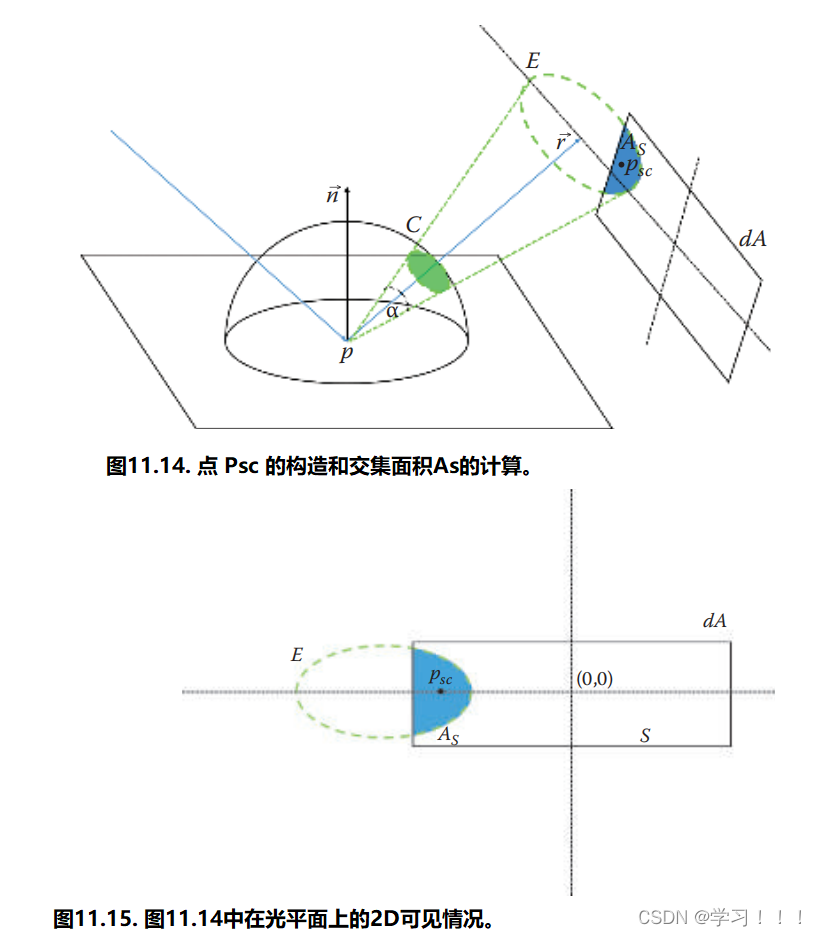
        我们成功地将该方法应用于各种镜面模型，如Phong，Blinn-Phong，Beckmann和GGX[Walter et al. 07]。然而，值得注意的是，锥体形状是对实际分布的三维形状的松散约束，其复杂性在不同的BRDF中变化。因此，锥体形状只是近似。在Phong的情况下，锥体实际上是完美匹配的。然而，在Blinn-Phong的情况下，由于使用了半向量，一个具有椭圆底面的金字塔或更复杂的形状将提供更紧密、更准确的边界。

        现在，我们已经有了镜面反射函数最重要样本的近似模型。在单区域光源的情况下，我们需要计算的是镜面反射函数在锥形区域内的积分。我们可以采用与第 11.3.3 节类似的推理和方法来近似计算最终结果。 同样，我们准备了一个不同的数据库，数值计算了积分，并估算了最重要的点。最后我们发现，积分极限区域的几何中心是估算无约束镜面积分的最佳点。我们称之为 Psc。因此，为了得到最终结果，我们必须计算 Psc 处单点光的镜面反射（p, ωo），并通过积分极限区域对结果进行归一化（见图 11.14）。

        为了简化问题，我们将转到光空间（参见图11.15），通过将我们的镜面锥体投影到光平面上来观察一个二维问题，即找到椭球体（投影后的镜面锥体）与给定光形状（在我们的案例中为圆盘或矩形，因为球体在只使用立体角进行计算时更容易解决）之间的交集面积。
 

面积镜面逼近算法: 这是用于逼近面积镜面积分的算法的伪代码（参见图11.14和图11.15）：

•    ◦ 对于每个着色点p，找到反射向量r。

•    ◦ 根据点p和光泽度g计算来自BRDF使用的镜面重要锥体顶角αBRDF(g)，其中αBRDF(g)根据用于建模镜面照明的BRDF确定。
•    ◦ 创建以点p为顶点，开口角为α的圆锥C，以矢量r为轴。
•    ◦ 把锥体C投影到面积光源L的光平面上，得到椭球体E。
•    ◦ 找到椭球体E与描述镜面光形状的函数S的交集面积AS。
•    ◦ 找到交集面积AS的几何中心Psc，即镜面积分的重要点。
•    ◦ 计算如果Psc是一个点光源时Specular(p, ωo)，因此得到矢量 PPsc。
•    ◦ 通过实际面积AS作为有效立体角微分来归一化结果。

将上述方法应用于方程（11.12）中可得：

将方程（11.19）中的立体角微分用AS标准化替代后，我们得到：
 

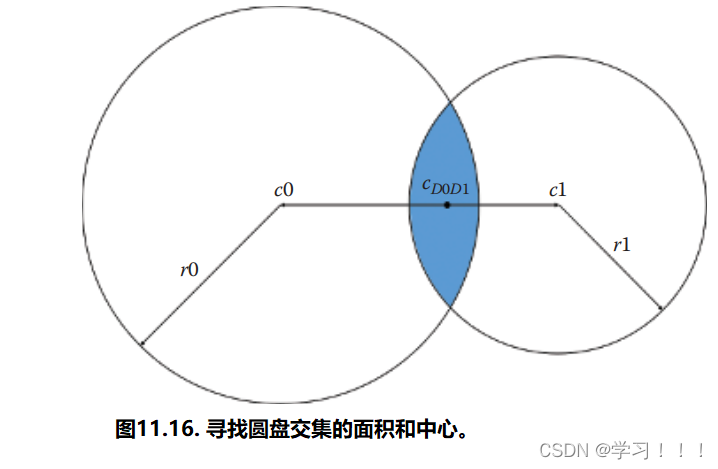
        对于特定的光源解算时，我们使用适用于光源类型的适当方法来计算AS。下一节将重点介绍各种光源形状与镜面重要锥体的交集面积逼近方法。

交集面积计算:  在运行时查找各种2D图形之间的交集面积是一项复杂的任务。在我们的案例中，我们需要考虑的是椭圆-圆盘或椭圆-矩形的相交面积。圆盘和矩形在光空间中是对齐轴的，并且以（0，0）为中心，因为它们表示实际的光形状。椭圆可以旋转。(看图11.14 和11.15) 为了简化着色器的复杂度，我们决定用一个简单的圆盘来近似一个椭球。计算两个圆盘或一个轴对齐框和一个圆盘的相交面积是一个相对容易解决的问题。在圆盘-圆盘相交的情况下，我们使用由[oat 06]提出的已知的平滑阶梯近似方法：
    

其中c0、r0、c1和r1分别是圆盘D0和D1的中心和半径。（看图11.16）

              

相交的几何中心（如果相交存在）由下式给出
 

方程(11.21)和(11.22)在c0位于(0, 0)的假设下简化。

        在矩形-圆盘相交的情况下，我们将圆盘视为一个面积与原始圆盘相同的正方形。因此，我们可以使用简单的轴对齐矩形-矩形相交数学方法。AR0R1和cR0R1由下式给出

 其中c0，d0，c1和d1分别是矩形R0和R1的中心点和尺寸，tl和br分别是左上和右下的相交角（假设欧几里德空间具有反向y轴，参见图11.17）。
 

        值得注意的是，只有基于径向对称概率分布函数（PDF）的模型才能获得准确的结果。如果我们在相交测试和积分计算期间剥离投影部分，通过将投影的椭圆替换为圆盘，我们不仅近似了最终结果，而且还限制了模型只适用于径向对称PDF。对于大多数基于半向量的微平面BRDF（公式(11.9)），镜面锥体的初始形状将类似于一个椭圆形底座，这将导致在光平面上积分为一个椭圆。

这是一种相当粗糙的近似方法; 然而，在与Phong、Blinn-Phong和GGX进行测试时，在通过使用具有径向对称光形状的概率分布函数进行视觉评估时，结果是足够好的（参见图11.18和11.19）。

 

这是一种相当粗糙的近似方法; 然而，在与Phong、Blinn-Phong和GGX进行测试时，在通过使用具有径向对称光形状的概率分布函数进行视觉评估时，结果是足够好的（参见图11.18和11.19）。

11.3.5 非均匀光源
        到目前为止，我们只考虑了光源的固定亮度Li(p, ωi)。现在我们改变这个假设，出于简单起见，假设光强度I在光源上是恒定的，并且Li(p, ωi)返回的是与波长相关的归一化值。从公式(11.11)和(11.12)的积分和11.3.3和11.3.4节的直觉出发，我们可以看到，为了获得正确的结果，我们可以通过在光源上变化的Li(p, ωi)进行预积分公式(11.11)和(11.12)，然后通过光源面积进行归一化。假设我们可以在运行时根据公式 (11.16) 和 (11.20) 近似计算漫反射和镜面积分，我们只需在漫反射和镜面积分的最重要点分别将这些结果乘以公式 (11.11) 和 (11.12) 中预先积分的归一化全积分即可。

    对于漫反射（公式(11.11)和(11.16)），我们需要积分

其中pd是光平面上法线为nl的点，r是离光源的距离。
 

        为了简化，我们假设遮挡不影响结果。然后，积分可以在一个三维查找表中进行预计算，该表以光空间中的pd.xy坐标和点p与pd之间的距离r为索引。可以根据计算积分时仍能产生视觉差异的最大距离对距离进行归一化处理。这样的最大距离可以通过解光形状的立体角（方程（11.3））来计算r而得出，而与cosθo无关，其中σ设置了立体角度权重的边界重要性：
                                                                        
                                                                                

    
对于大于 r max 的距离，立体角将太小，结果积分在视觉上不会有太大的变化。
        查找表的每个Z层都包含点pd的漫反射积分，设置在光空间中的pd.xy坐标上，距离光平面max(r/rmax, 1)。最后，完整的漫反射积分近似为
                    

---

        对于镜面（方程（11.12））的情况，我们需要积分
 

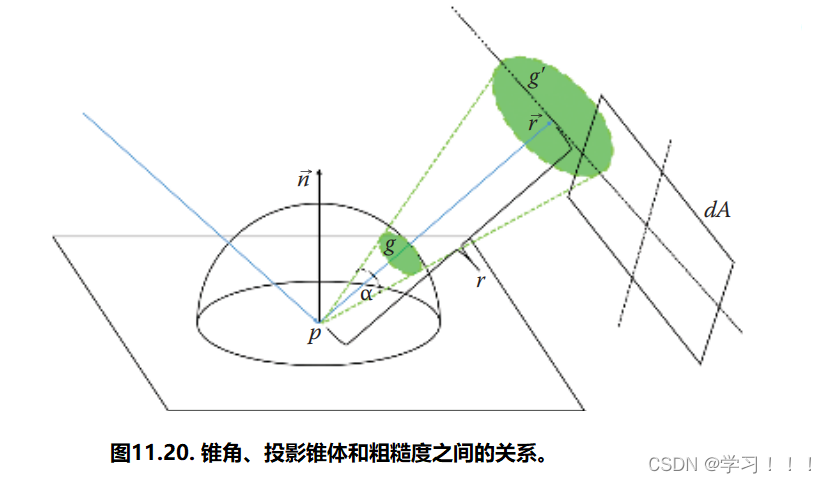
其中p是正在着色的点，Psc是具有定义为表面粗糙度的最重要的镜面积分点。不幸的是，这样的表示需要一个四维查找表。我们希望摆脱p点的四个维度。根据第11.3.4节的推理，我们知道积分实际上将取决于重要采样半径的投影锥体。我们还知道如何创建函数，根据给定的BRDF计算出表面粗糙度的镜面重要锥体顶角（方程（11.17）和（11.18））。投影重要锥体半径取决于到光的距离r和锥体开口角α（参见图11.20）。因此，我们可以根据方程（11.25）为点Psc和新的粗糙度g'计算积分，其中



为了使这个假设可行，我们必须仅限于径向对称的概率密度函数：
 

其中h垂直于视线方向ωo。这实际上迫使我们使用Phong作为我们的D函数

        在这些假设的基础上，我们可以将方程（11.27）计算为一个三维查找表，该表由光空间中的Psc.xy坐标和使用方程（11.26）计算的g'索引，该方程针对所使用的BRDF进行了推导。
        最后，完整的镜面积分近似为
 

        值得注意的是，根据选择，函数DFG可能取决于g或其他表面参数。除了已经包含的g之外，每个额外的参数都会给我们的查找表增加一个维度，或者必须被分解出来。这完全取决于镜面模型的最终选择。

11.3.6 解决面光BRDF
        我们提出了一个基于当前已知和经过深入研究的BRDF的面基光照模型的高效推导框架。最终的光照模型应遵循第11.3节中的所有步骤，选择特定的DFG函数，并根据它们直接推导出额外的参数。然后，可以为各种光源（方程（11.16）和（11.20））包括彩色、非均匀光源（方程（11.24）和（11.28））近似计算每个点的漫反射和镜面光照。参见图11.21、11.22和11.23。
 

11.4 实现
11.4.1 简介
        本章从多个方面的思考中融合并使用，成为《杀戮地带:暗影坠落》中光照模型的基础。光照渲染引擎在实时屏幕空间反射和局部环境反射探针上有很大依赖。这两种解决方案只能有效地支持基于辐射对称分布的镜面反射（Phong）。动态基于纹理的光源的一个要求是能够与现有的基于图像的系统完美融合。基本上，我们希望能够在距离上无视觉伪影地在动态面光、基于图像的光卡和立方体贴图反射之间切换。我们还希望支持解析形状光源，以实现最高的视觉质量和高级材质反射模型。

11.4.2 动机

        我们使用Cook-Torrance BRDF作为反射模型的基础。归一化的Blinn-Phong被用作分布函数。Fresnel和几何项根据Smith-Schlick的近似公式进行计算，与Blinn-Phong进行匹配和归一化。我们还准备了此BRDF的径向对称版本。它被重新调整为使用Phong作为基础，并尽可能接近参考解决方案进行归一化和匹配。

                

        所有光源都使用第11.3.3节中介绍的相同的漫反射积分近似推理。每个光源，根据光形状函数的不同，实现方程（11.16）或方程（11.24）来近似计算漫反射积分。这包括太阳光、全向光和具有球体、圆盘或矩形光形状的聚光灯。

        标准的解析动态光源，根据光形状函数的不同，实现方程（11.20）来近似计算镜面积分。在纹理区域光源的情况下，我们仅支持具有基于Phong的BRDF的矩形光源。

        基于Phong的Cook-Torrance也用于基于图像的光照卷积和基于纹理的区域光源。与用于立方体贴图生成的已知方法类似[Lazarov 11]，我们基于我们的基于Phong的BRDF构建核，并为不同的镜面锥体宽度生成多个mip-map级别的立方体贴图（参见图11.24）。类似于第11.3.5节中数学上描述的推理，我们将其应用于生成与第11.3.5节中描述的相似方式索引的纹理中的图像光卡。

不同的光形状实现。《Killzone》渲染器支持以下光形状：球体、矩形和圆盘。所有光源都遵循磁盘光源实现设置的框架。它们只需要对负责形状最接近点或归一化立体角的代码进行轻微的更改。因此，我们能够在不同的光形状之间高效地共享代码。
 

        值得注意的是，球形扩散积分的实现可以通过解析积分来大大简化，因为它具有仅依赖于光源位置和半径的闭合形式。球形镜面积分也可以通过仅使用固体角微分来进行优化。无需将计算投影到光空间中，因为球形形状在3D中很容易定义。此外，投影的固体角等于固体角，因为球体始终对应相同的固体角，与视角和方向无关。

        非均匀光源的实现。我们支持使用矩形形状作为基础的基于纹理的光源。我们应用了第11.3.5节的推理，直接计算并存储预计算数据在2D纹理的mip-map中。初始光强度由游戏中的拟像渲染系统生成的纹理或艺术家手绘提供。计算得到的值被归一化并存储在两个压缩的RGB8格式纹理中（参见图11.25和11.26）。运行时，矩形光源评估扩散和镜面积分，并将结果乘以类似于第11.3.5节中描述的纹理中的预计算部分积分。

11.5 结果讨论
        在《杀戮地带:暗影坠落》的制作过程中，仅使用面积光源证明了它是基于物理的渲染流水线的重要支柱。由于提出的模型，我们能够统一来自不同来源（分析或基于图像）的光照，保持类似的响应和质量。我们的艺术制作流程能够在一个封闭的审查环境中生成作品，准备为HDR预集成的BRDF立方体贴图，并期望在游戏中获得类似的高质量结果（见图11.27和11.28）。
 

        由于材质和光照处理的隐式分离，团队可以高效地在级别资产上工作，而不会干扰光照和环境部门。以前，这种冲突是不可避免的，因为环境艺术家往往倾向于调整资产以模拟物理上更大的光源（例如通过改变粗糙度）。这种习惯往往导致在不同的游戏场景中出现重复的资产。
 

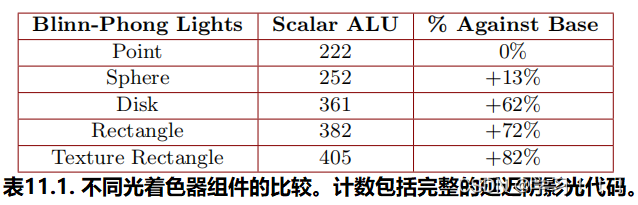
        面积光照模型在次世代主机Playstation 4 GPU上表现出了高效性。模型本身在ALU操作上很重（见表11.1），这在我们的案例中有助于分摊从带宽密集的G缓冲区和阴影贴图中获取多个纹理的等待时间。因此，与更标准的基于点的光照模型（如Blinn-Phong）相比，我们并没有遇到明显的减速。
 

        不幸的是，我们在模型推导过程中采取的一些捷径在使用基于Blinn-Phong的BRDF矩形面光源时会产生一些伪影。由于这些情况，我们决定只使用矩形形状与基于Phong的BRDF完全匹配，因为它更适用于非径向对称光源形状的近似。

    
                         

     

11.6 进一步研究
        在不久的将来，我们希望专注于改进镜面积分的归一化部分，目前由于圆盘逼近（第11.3.4节），其在视觉质量上不如参考解决方案。我们对于Blinn-Phong以及其他具有类似基础的微表面分布（如最近流行的GGX）的良好逼近特别感兴趣。

        为了做到这一点，我们需要找到一种高效的方法来找到旋转椭圆和圆盘或矩形之间的交点。

        我们还认为，当使用非径向对称的PDF时，矩形光源的镜面近似需要进行更多的研究。目前，最重要点的当前算法可能在光源的旋转角度与PDF的各向异性方向正交时产生严重伪影。一个合适的搜索算法需要考虑各向异性方向。值得注意的是，即使在其当前形式下，对于接近正方形的矩形形状，伪影可能是可接受的（见图11.29和11.30）。
        
       

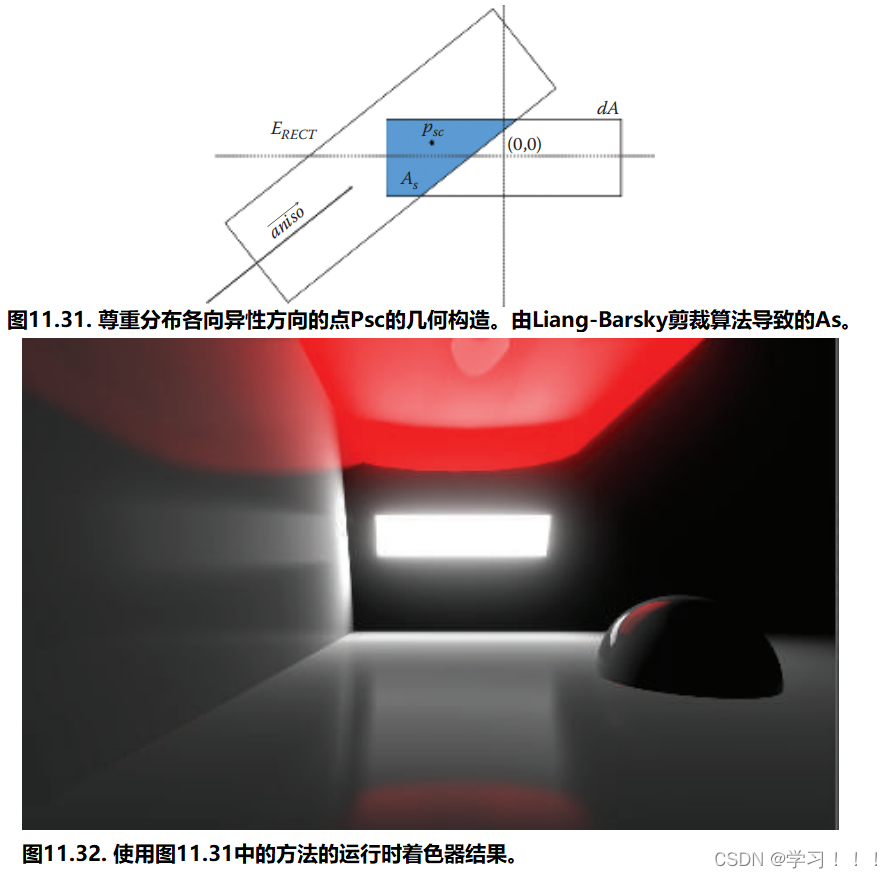
        一个提出的启发式方法是将投影的镜面锥体视为一个沿着各向异性方向延伸的细长矩形。这种形状的改变可以是动态的，根据特定的BRDF计算。然后，镜面采样的最重要点将是镜面矩形与光源形状的交点的几何中心。交点面积也可以用作归一化的一部分（见公式（11.20））。

        我们通过解析找到表示光源形状和投影的镜面锥体交点的多边形来为矩形光源原型化了这种方法。为了在运行时找到交点，我们使用了GPU优化版本的Liang-Barsky裁剪算法[Liang and Barsky 84]。将光源形状矩形视为裁剪窗口，然后将表示投影的镜面锥体与之进行裁剪。最终结果是表示平面、非自交多边形的顶点数组。为了找到多边形的面积，我们使用了高斯公式计算任意多边形的面积。

        不幸的是，繁忙的制作计划阻止了在这个有前途的方向上进行进一步研究。图11.31以参考基于着色器的解决方案结果（图11.32）的几何方式展示了这个提出的想法。

        另一个提出的研究领域包括对基于纹理的面光源支持非径向对称的PDF。我们尝试了多采样方法和在运行时近似PDF，但对于我们的实时预算来说，这被证明是太昂贵的。

11.7 结论
          我们提供了一个经过测试的框架，用于以目前研究的 BRDF 为起点，开发各种基于物理、基于区域的照明模型。实践证明，该框架对于《杀戮地带:暗影坠落》游戏项目的渲染引擎是稳健和高效的。
    

        我们希望提出的想法能为其他研究人员和开发人员提供解决区域照明问题的工具，并进一步扩展这一概念。未来，我们希望基于区域的照明将成为现代视频游戏的实际标准，为基于物理的材料反射模型提供统一、可预测的照明解决方案。

参考：