数字滤波器的技术指标

本文主要是介绍数字滤波器的技术指标，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

数字滤波器的技术指标一般可以用幅频特性和相频特性指标来给出。
设数字滤波器的频率响应为：
$$H({\mathrm{e}}^{\mathrm{j}\omega })=\mid H({\mathrm{e}}^{\mathrm{j}\omega })\mid {\mathrm{e}}^{\mathrm{j}\phi (\omega )}$$
式中:|H(e^jω )|表征幅频特性,φ(ω)表征相频特性。幅频特性表示信号通过该滤波器后各频率成分衰减情况,而相频特性反映了各频率成分通过滤波器后在时间上的延时情况。因此,即使两个滤波器幅频特性相同,而相频特性不一样,对相同的输入,滤波器输出的信号波形也是不一样的。

幅频特性指标

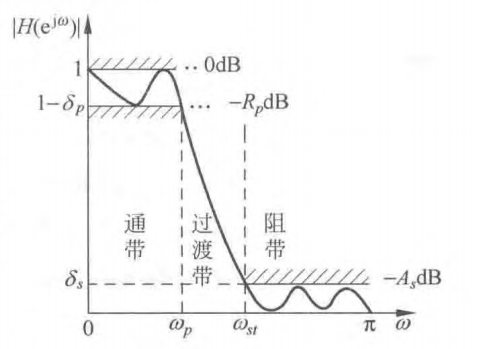
一个实际数字低通滤波器的幅频特性及技术指标如上图所示。与理想低通滤波器相比可以看出,实际的滤波器有明显的不同:

一是通带和阻带内不再平坦,都存在一定的波动;

二是在通带和阻带之间的切换不再是直线下降的而是有一个过渡带,幅频特性逐步从大变小。

这是因为理想低通滤波器的幅频特性从通带到阻带之间有突变,将导致其物理上是不可实现的。为了物理上可实现,实际设计的滤波器在通带与阻带之间应有一定宽度的过渡带,以便允许幅频特性平滑地下降。同时,通带和阻带内不可能严格为1或0,应允许有一定的偏差,容许偏差的极限称为容限。

---

参数	符号
通带截止频率	ωp
阻带截止频率	ωs
通带容限	δp
阻带容限	δs
通带允许的最大衰减(波纹)	Rp
阻带应达到的最小衰减	As
3dB截止频率	ωc

频段[0,ω_p]称为通带,ω_p 称为通带截止频率,δp 称为通带容限,在通带内幅频特性要求为：
$$1-{\delta }_{{}_p}⩽\mid H\left({\mathrm{e}}^{\mathrm{j}\omega }\right)\mid ⩽1,\mid \omega \mid ⩽{\omega }_{{}_p}$$
频段[ω_s,π]称为阻带,ω_s 称为阻带截止频率,δs 称为阻带容限,在阻带内幅频特性要求为：
$$\mid H({\mathrm{e}}^{\mathrm{j}\omega })\mid ⩽{\delta }_{\mathrm{s}},{\omega }_{\mathrm{st}}⩽\mid \omega \mid ⩽\pi$$
通带容限δ_p 和阻带容限δ_s 描述了通带和阻带内幅频特性的波动程度。在工程应用中,这两个参数常用其dB(分贝)值来描述,通带允许的最大衰减(波纹)Rp分贝(dB)以及阻带应达到的最小衰减As分贝(dB)(已归一化为|H(e^jw)|_max=1),要求：
$$\begin{array}{rl}& R_{\rho }⩾20\lg \frac{\mid H({\mathrm{e}}^{\mathrm{j}\omega }){\mid }_{\max }}{\mid H({\mathrm{e}}^{\mathrm{j}{\omega }_{\mathrm{p}}})\mid }=-20\lg \mid H({\mathrm{e}}^{\mathrm{j}{\omega }_p})\mid =-20\lg (1-{\delta }_p)(\mathrm{dB})\\ & A_s⩽20\lg \frac{\mid H({\mathrm{e}}^{\mathrm{j}\omega }){\mid }_{\max }}{\mid H({\mathrm{e}}^{\mathrm{j}{\omega }_{st}})\mid }=-20\lg \mid H({\mathrm{e}}^{\mathrm{j}{\omega }_{st}})\mid =-20\lg {\delta }_s(\mathrm{dB})\end{array}$$
如果用分贝(dB)表示增益,则把|H(e^jw)|_max=1[一般是指w=0处(|H(e^j0)|= 1]的增益[20lg|H(e^jw)|_max =0]称为0dB。则通带边沿(w= w_p)处增益为-R_p,而其衰减则称为R_p(R_p为正数,单位为dB);同样阻带起始频率w_s处的增益为-A_s,而其衰减则为A_s,(A,也为正数,单位为dB)。

若要求w=w_p时,$\mid H({\mathrm{e}}^{\mathrm{j}{\omega }_p})\mid =1-{\delta }_p=\frac{1}{\sqrt{2}}=0.707$

则在w=w_p处衰减为
$$201g\left[\frac{{\left|H(e^{j_{{\omega }_m}})\right|}_{\max }}{\left|H(e^{j_{{\omega }_p}})\right|}\right]=-201g|H(e^{j_{{\omega }_p}})|=-20\lg (1-{\delta }_s)=3\mathrm{dB}$$
即在w=w_p处增益为-3dB(衰减为3dB)[把|H(e^jw)|的最大值的增益定为0dB]。在w=w_p处的衰减,也可以要求是其他分贝数,例如1dB、2dB等。

---

上图画出了同一滤波器的幅频特性绝对值和相对值(dB值)曲线。一般来说,在工程应用中通常要求As>40dB,即对噪声、干扰等无用信号的抑制作用要大于40dB,此时对应的幅频特性绝对值小于0.01。显然,此时图(a)中显示的幅频特性绝对值曲线不便于观察阻带响应曲线(近似与零值坐标轴重合),而图(b)清楚地显示出阻带-40dB以下的响应曲线,这样便于观察和描述滤波器频率响应特性。所以,常用幅频特性的衰减dB值描述设计指标。
频段[ω_p,ω_s]称为过渡带,Δω=ω_s-ω_p 表示过渡带宽,在这个过渡带内幅频特性平滑地从通带下降到阻带。对比理想滤波器,从理论上来说过渡带越窄越好。但当通带和阻带指标不变时,过渡带越窄,要求的滤波器阶数越高,付出的代价也越高。

异

在《数字信号处理原理与应用》书中对通带最大衰减的计算有所不同，采用w=0为归一基准。

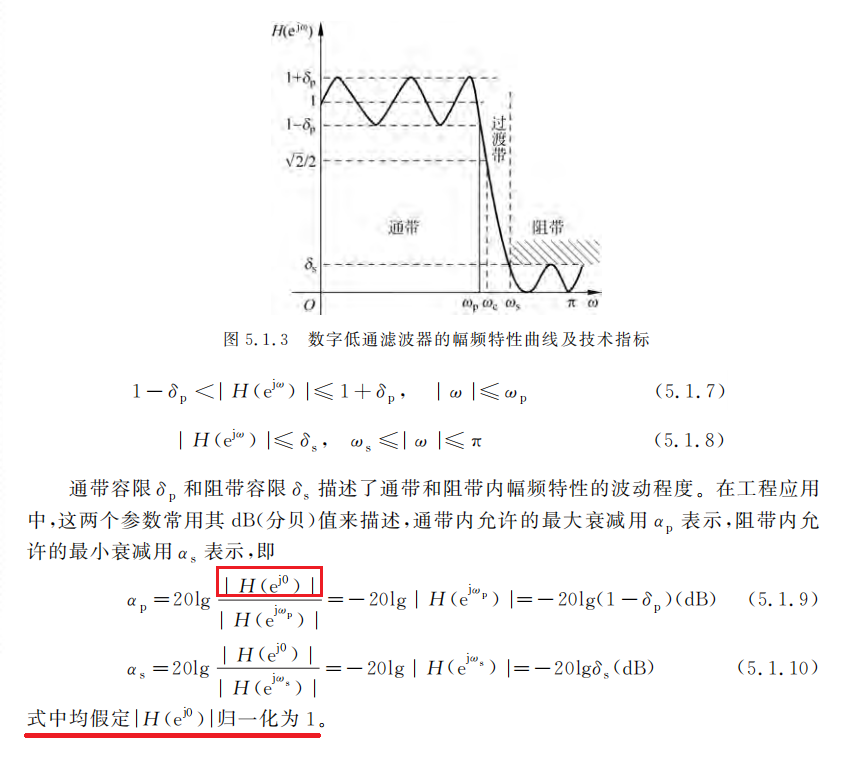
部分书籍中计算公式：
$$a_{{}_p}=20\lg \frac{1+{\delta }_{{}_p}}{1-{\delta }_{{}_p}},$$

需要注意区分。

相频特性指标

数字滤波器的相频特性可以表示为:
$$\phi (\omega )=\text{arg}\left[H\left({\mathrm{e}}^{\mathrm{j}\omega }\right)\right]$$
式中:arg[●]表示取相位操作。

数字滤波器的相频特性表征了输人信号各频率成分通过滤波器后在时间上的延时情况。一般来说，如果滤波器用于对相位要求不敏感的场合时，如语音通信等,设计滤波器可以只考虑幅频特性。而对于一些对输出波形有要求的应用场景,如波形传输、图像信号处理等,必须要同时考虑幅频和相频特性。此时,要求设计的滤波器除了具有所期望的幅频特性外,还应具有线性相位。

各型滤波器的幅度响应

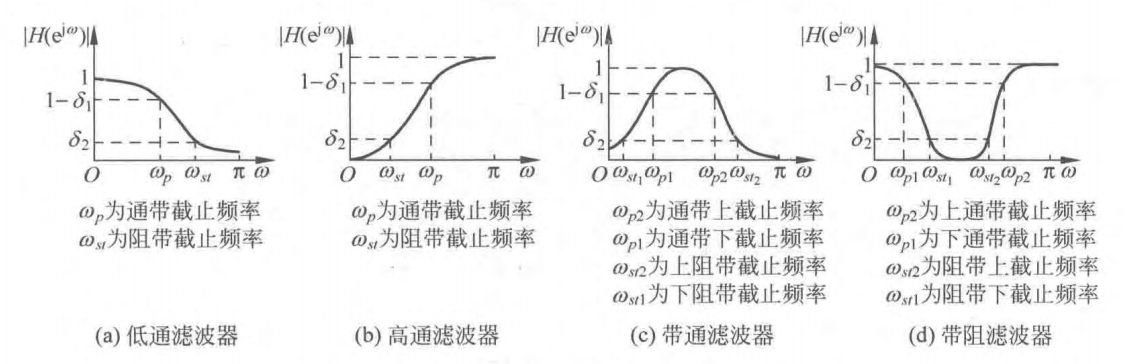
表征数字滤波器频率响应特性的三个参量

(1) 幅度平方响应

(2) 相位响应

(3) 群延迟响应

参考:
《数字信号处理教程》程佩青。
《数字信号处理原理与应用》

这篇关于数字滤波器的技术指标的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---