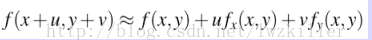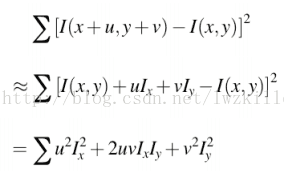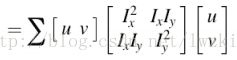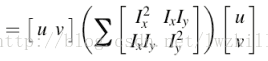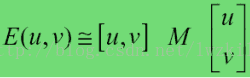本文主要是介绍12.1 关键点提取------Harris原理及代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、原理
该原理看了Harris角点检测原理详解-CSDN博客的博文,在这里写一遍是作为笔记,以供后参考。
1.什么是角点
角点就是图片中的一些突变的点,如下图所示。图中的点都是菱角分明的一些凸出来或凹进去的点。

我们可以直观的概括下角点所具有的特征:
>轮廓之间的交点;
>对于同一场景,即使视角发生变化,通常具备稳定性质的特征;
>该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化;
2. 角点检测算法基本思想是什么?
算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么我们可以认为该窗口中存在角点。
3.如何用数学方法去刻画角点特征?
当窗口发生[u,v]移动时,那么滑动前与滑动后对应的窗口中的像素点灰度变化描述如下:
公式解释:
>[u,v]是窗口的偏移量
>(x,y)是窗口内所对应的像素坐标位置,窗口有多大,就有多少个位置
>w(x,y)是窗口函数,最简单情形就是窗口内的所有像素所对应的w权重系数均为1。但有时候,我们会将w(x,y)函数设定为以窗口中心为原点的二元正态分布。如果窗口中心点是角点时,移动前与移动后,该点的灰度变化应该最为剧烈,所以该点权重系数可以设定大些,表示窗口移动时,该点在灰度变化贡献较大;而离窗口中心(角点)较远的点,这些点的灰度变化几近平缓,这些点的权重系数,可以设定小点,以示该点对灰度变化贡献较小,那么我们自然想到使用二元高斯函数来表示窗口函数,这里仅是个人理解,大家可以参考下。
所以通常窗口函数有如下两种形式:
根据上述表达式,当窗口处在平坦区域上滑动,可以想象的到,灰度不会发生变化,那么E(u,v) = 0;如果窗口处在比纹理比较丰富的区域上滑动,那么灰度变化会很大。算法最终思想就是计算灰度发生较大变化时所对应的位置,当然这个较大是指针任意方向上的滑动,并非单指某个方向。
4.E(u,v)表达式进一步演化
首先需要了解泰勒公式,任何一个函数表达式,均可有泰勒公式进行展开,以逼近原函数,我们可以对下面函数进行一阶展开(如果对泰勒公式忘记了,可以翻翻本科所学的高等数学)
那么,
所以E(u,v)表达式可以更新为:
这里矩阵M为,
5.矩阵M的关键性
难道我们是直接求上述的E(u,v)值来判断角点吗?Harris角点检测并没有这样做,而是通过对窗口内的每个像素的x方向上的梯度与y方向上的梯度进行统计分析。这里以Ix和Iy为坐标轴,因此每个像素的梯度坐标可以表示成(Ix,Iy)。针对平坦区域,边缘区域以及角点区域三种情形进行分析:
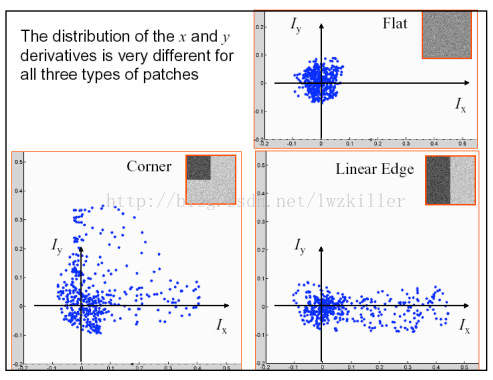
下图是对这三种情况窗口中的对应像素的梯度分布进行绘制:
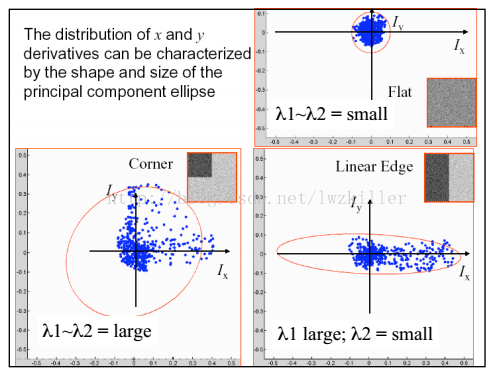
如果使用椭圆进行数据集表示,则绘制图示如下:
不知道大家有没有注意到这三种区域的特点,平坦区域上的每个像素点所对应的(IX,IY)坐标分布在原点附近,其实也很好理解,针对平坦区域的像素点,他们的梯度方向虽然各异,但是其幅值都不是很大,所以均聚集在原点附近;边缘区域有一坐标轴分布较散,至于是哪一个坐标上的数据分布较散不能一概而论,这要视边缘在图像上的具体位置而定,如果边缘是水平或者垂直方向,那么Iy轴方向或者Ix方向上的数据分布就比较散;角点区域的x、y方向上的梯度分布都比较散。我们是不是可以根据这些特征来判断哪些区域存在角点呢?
虽然我们利用E(u,v)来描述角点的基本思想,然而最终我们仅仅使用的是矩阵M。让我们看看矩阵M形式,是不是跟协方差矩阵形式很像,像归像,但是还是有些不同,哪儿不同?一般协方差矩阵对应维的随机变量需要减去该维随机变量的均值,但矩阵M中并没有这样做,所以在矩阵M里,我们先进行各维的均值化处理,那么各维所对应的随机变量的均值为0,协方差矩阵就大大简化了,简化的最终结果就是矩阵M,是否明白了?我们的目的是分析数据的主要成分,相信了解PCA原理的,应该都了解均值化的作用。
如果我们对协方差矩阵M进行对角化,很明显,特征值就是主分量上的方差,这点大家应该明白吧?不明白的话可以复习下PCA原理。如果存在两个主分量所对应的特征值都比较大,说明什么? 像素点的梯度分布比较散,梯度变化程度比较大,符合角点在窗口区域的特点;如果是平坦区域,那么像素点的梯度所构成的点集比较集中在原点附近,因为窗口区域内的像素点的梯度幅值非常小,此时矩阵M的对角化的两个特征值比较小;如果是边缘区域,在计算像素点的x、y方向上的梯度时,边缘上的像素点的某个方向的梯度幅值变化比较明显,另一个方向上的梯度幅值变化较弱,其余部分的点都还是集中原点附近,这样M对角化后的两个特征值理论应该是一个比较大,一个比较小,当然对于边缘这种情况,可能是呈45°的边缘,致使计算出的特征值并不是都特别的大,总之跟含有角点的窗口的分布情况还是不同的。
注:M为协方差矩阵,需要大家自己去理解下,窗口中的像素集构成一个矩阵(2*n,假设这里有n个像素点),使用该矩阵乘以该矩阵的转置,即是协方差矩阵
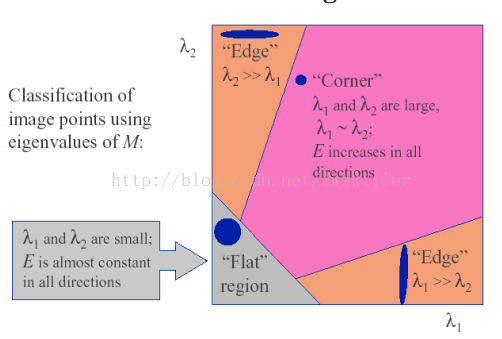
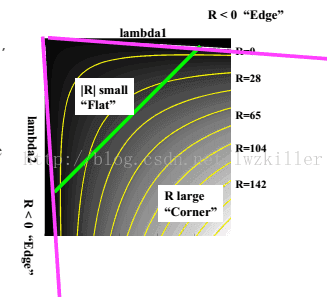
因此可以得出下列结论:
>特征值都比较大时,即窗口中含有角点
>特征值一个较大,一个较小,窗口中含有边缘
>特征值都比较小,窗口处在平坦区域
6. 如何度量角点响应?
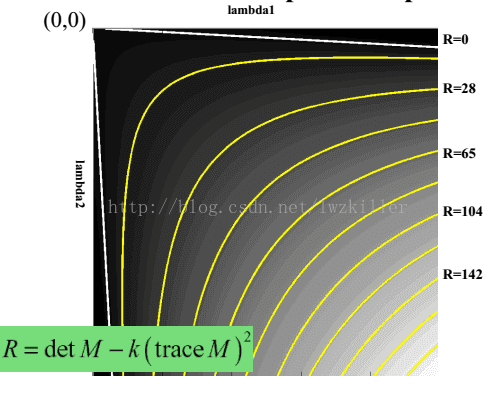
通常用下面表达式进行度量:
其中k是常量,一般取值为0.04~0.06,这个参数仅仅是这个函数的一个系数,它的存在只是调节函数的形状而已。
但是为什么会使用这样的表达式呢?一下子是不是感觉很难理解?其实也不难理解,函数表达式一旦出来,我们就可以绘制它的图像,而这个函数图形正好满足上面几个区域的特征。 通过绘制函数图像,直观上更能理解。绘制的R函数图像如下:
二、代码实现
1.C++代码实现
#include <vtkAutoInit.h>
VTK_MODULE_INIT(vtkRenderingOpenGL);
VTK_MODULE_INIT(vtkInteractionStyle);
#include <iostream>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/common/io.h>
#include <pcl/features/normal_3d.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <pcl/console/time.h>
#include <pcl/keypoints/harris_3D.h>//harris
using namespace pcl;int main(int argc, char **argv)
{//读取点云pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);if (pcl::io::loadPCDFile<pcl::PointXYZ>("test.pcd", *cloud) == -1){PCL_ERROR("Cloudn't read file!");system("pause");return -1;}//Harris关键点提取float r_normal;float r_keypoint;r_normal = 0.6;r_keypoint = 0.8;typedef pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZI> ColorHandlerT3;pcl::PointCloud<pcl::PointXYZI>::Ptr Harris_keypoints(new pcl::PointCloud<pcl::PointXYZI>()); pcl::HarrisKeypoint3D<pcl::PointXYZ,pcl::PointXYZI,pcl::Normal>* harris_detector = new pcl::HarrisKeypoint3D<pcl::PointXYZ, pcl::PointXYZI, pcl::Normal>;harris_detector->setRadius(r_normal); //设置法向量估算的半径harris_detector->setRadiusSearch(r_keypoint);
//设置关键点估计的近邻搜索半径harris_detector->setInputCloud(cloud);harris_detector->compute(*Harris_keypoints);cout<< "Harris_keypoints的大小是" <<Harris_keypoints->size()<< endl;//显示harris关键点pcl::visualization::PCLVisualizer viewer("clouds");viewer.setBackgroundColor(255,255, 255); viewer.addPointCloud(Harris_keypoints,ColorHandlerT3(Harris_keypoints,0.0, 0.0, 255.0),
"Harris_keypoints"); viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,8, "Harris_keypoints");viewer.addPointCloud(cloud,"cloud"); viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR,0,0, 0, "cloud"); viewer.setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE,
2, "cloud");viewer.setCameraPosition(0,0, 0, 0, 156, -20, 0, 0, 1, 0);//设置相机位置,焦点,方向viewer.spin();return 0;
}2.python代码实现
import cv2
import numpy as np
import matplotlib
import math
from matplotlib import pyplot as plt #根据一阶锐化算子,求x,y的梯度,显示锐化图像
#读取图片
filename = 'girl.jpg'
tu = cv2.imread(filename)#转换为灰度图
gray = cv2.cvtColor(tu, cv2.COLOR_RGB2GRAY)#获取图像属性
print '获取图像大小: '
print gray.shape
print '\n'#打印数组gray
print '灰度图像数组:\n %s \n \n' % (gray)#输出n*n的数组
#print gray[:2,:2]#转换为矩阵
m = np.matrix(gray)#计算x方向的梯度的函数(水平方向锐化算子)
delta_h = m
def grad_x(h):a = int(h.shape[0])b = int(h.shape[1])for i in range(a):for j in range(b):if i-1>=0 and i+1<a and j-1>=0 and j+1<b:c = abs(int(h[i-1,j-1]) - int(h[i+1,j-1]) + 2*(int(h[i-1,j]) - int(h[i+1,j])) + int(h[i-1,j+1]) - int(h[i+1,j+1]))
# print cif c>255:
# print cc = 255delta_h[i,j] = celse:delta_h[i,j] = 0print 'x方向的梯度:\n %s \n' %delta_hreturn delta_h##计算y方向的梯度的函数(水平方向锐化算子)
def grad_y(h):a = int(h.shape[0])b = int(h.shape[1])for i in range(a):for j in range(b):if i-1>=0 and i+1<a and j-1>=0 and j+1<b:c = abs(int(h[i-1,j-1]) - int(h[i-1,j+1]) + 2*(int(h[i,j-1]) - int(h[i,j+1])) + (int(h[i+1,j-1]) - int(h[i+1,j+1]))) #注意像素不能直接计算,需要转化为整型
# print cif c > 255:c = 255delta_h[i,j] = celse:delta_h[i,j] = 0print 'y方向的梯度:\n %s \n' %delta_hreturn delta_h# Laplace 算子
img_laplace = cv2.Laplacian(gray, cv2.CV_64F, ksize=3) dx = np.array(grad_x(gray))
dy = np.array(grad_y(gray))#dxy = dx + dy
#print 'dxy1:'
#print dxyA = dx * dx
B = dy * dy
C = dx * dyprint A
print B
print CA1 = A
B1 = B
C1 = CA1 = cv2.GaussianBlur(A1,(3,3),1.5)
B1 = cv2.GaussianBlur(B1,(3,3),1.5)
C1 = cv2.GaussianBlur(C1,(3,3),1.5)print A1
print B1
print C1a = int(gray.shape[0])
b = int(gray.shape[1])R = np.zeros(gray.shape)
for i in range(a):for j in range(b):M = [[A1[i,j],C1[i,j]],[C1[i,j],B1[i,j]]]R[i,j] = np.linalg.det(M) - 0.06 * (np.trace(M)) * (np.trace(M))print Rcv2.namedWindow('R',cv2.WINDOW_NORMAL)
cv2.imshow('R',R)cv2.waitKey(0)
cv2.destroyAllWindows()
这篇关于12.1 关键点提取------Harris原理及代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!