本文主要是介绍【JZOJ6310】Global warming【线段树】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
题目大意:
题目链接:https://jzoj.net/senior/#main/show/6310
给定整数 n n n和 x x x,以及一个大小为 n n n的序列 a a a。
你可以选择一个区间 [ l , r ] [l,r] [l,r],然后令 a [ i ] + = d ( l < = i < = r ) a[i]+=d(l<=i<=r) a[i]+=d(l<=i<=r),其中 d d d满足 ∣ d ∣ < = x |d|<=x ∣d∣<=x。
要求最大化 a a a的最长上升子序列的长度,并输出该值。
思路:
首先有一个显然的性质:如果我们要把一段区间增加,那么显然这段区间右端点为 n n n时最优。
因为如果我们要增加区间 [ l , r ] [l,r] [l,r],那么如果我们把 r r r往右移一位,显然不会把答案变小。所以 r r r就可以移至最右。
那么这样我们就可以证明出如果区间 [ l , n ] [l,n] [l,n]需要上移,那么显然往上移动越多可以对答案造成更大的贡献。所以我们移动就将一段区间移动 x x x格。
那么如果我们需要把区间 [ l , r ] [l,r] [l,r]往下移动呢?和前面一样,显然把区间扩张成 [ 1 , r ] [1,r] [1,r]会最优,那么把 [ 1 , r ] [1,r] [1,r]往下移动就相当于把 [ r + 1 , n ] [r+1,n] [r+1,n]向上移动。所以可以不用处理。
同理,如果取原来的 L I S LIS LIS(不移动任何)也就相当于全部移动,所以也可以不用再去计算了。
那么如何计算呢?
假设现在处理 L I S LIS LIS末位为 i i i的情况,那么我们就要在 [ 0 , i − 1 ] [0,i-1] [0,i−1]中找到一个权值不超过 a [ i ] a[i] a[i]且 f [ i ] f[i] f[i]尽量大
的来转移。
那么我们可以建立一棵权值线段树,区间 [ l , r ] [l,r] [l,r]表示权值在 [ l , r ] [l,r] [l,r]中的 f f f的最大值。这样从前往后 / / /从后往前做时只要先转移再插入即可。
那么我们就枚举在哪一个位置开始加 x x x,然后求出这个位置前后的 L I S LIS LIS,一加就是答案。
这道题 x ≤ 1 0 9 x\leq 10^9 x≤109,所以动态开点就行了。
但是这样会
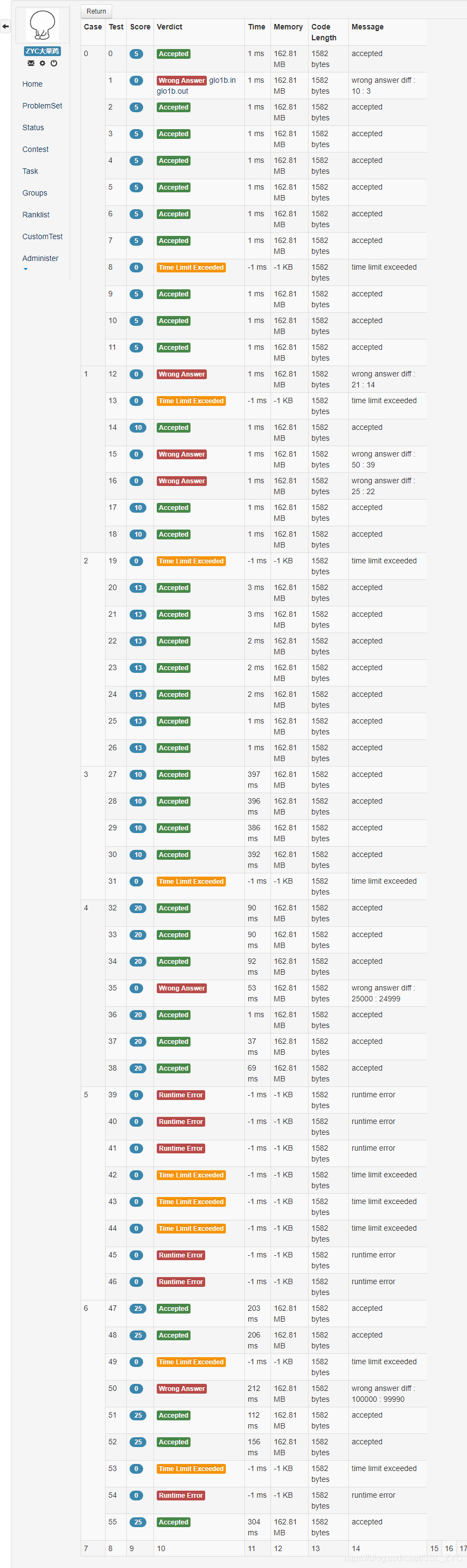
愉快的每一个 s u b t e s k subtesk subtesk搜错了至少一个
c o d e 2.0 code2.0 code2.0
我们发现其中很多位置 R E , W A RE,WA RE,WA,然后
哦权值线段树的空间复杂度是 O ( n log m ) O(n\log m) O(nlogm)啊。
于是把空间开大 30 + 30+ 30+倍。
然后
c o d e 3.0 code3.0 code3.0
输出了一下空间

于是就开始了漫长的卡空间之路。。。
- 我们发现,开两棵线段树分别计算两次是没必要的,所以我们就删掉一棵线段树,两次计算之间清零即可。
- 清零的标记占了 1 4 \frac{1}{4} 41的空间,考虑直接暴力重构整棵树。
试探性的把树的大小缩小
最终,线段树大小开到 O ( 200000 × 110 ) O(200000\times 110) O(200000×110)时,空间总算卡进了 259000 k b 259000kb 259000kb!!
c o d e 4.0 code4.0 code4.0
调试了一下,发现过程中出现了负数。
原来是因为 a i , x ≤ 1 0 9 a_i,x\leq 10^9 ai,x≤109,最大在线段树内可能出现的数为 2 × 1 0 9 2\times 10^9 2×109,所以线段树开到 2 × 1 0 9 2\times 10^9 2×109后, m i d = n o w l + n o w r 2 mid=\frac{nowl+nowr}{2} mid=2nowl+nowr就炸了 i n t int int。。。
m d md md因为这些我调试了一下午,还不如去打离散化的线段树。
时间复杂度 O ( n log n ) O(n\log n) O(nlogn),常数超级无敌大。
代码:
#include <cstdio>
#include <string>
#include <algorithm>
using namespace std;
typedef long long ll;const int N=200010,Inf=2e9;
int n,m,ans,root,a[N],f[N];struct Treenode
{int lc,rc,maxn;
};struct Tree
{Treenode tree[N*110];int tot;void clr(int x){if (tree[x].lc) clr(tree[x].lc);if (tree[x].rc) clr(tree[x].rc);tree[x].lc=tree[x].rc=tree[x].maxn=0;}int ask(int &x,int nowl,int nowr,int l,int r){if (l>r) return 0;if (!x) x=++tot;if (nowl==l && nowr==r) return tree[x].maxn;int mid=((ll)nowl+(ll)nowr)>>1;if (r<=mid) return ask(tree[x].lc,nowl,mid,l,r);if (l>mid) return ask(tree[x].rc,mid+1,nowr,l,r);return max(ask(tree[x].lc,nowl,mid,l,mid),ask(tree[x].rc,mid+1,nowr,mid+1,r));}void insert(int &x,int nowl,int nowr,int k,int val){if (!x) x=++tot;if (nowl==k && nowr==k){tree[x].maxn=max(tree[x].maxn,val);return;}int mid=((ll)nowl+(ll)nowr)>>1;if (k<=mid) insert(tree[x].lc,nowl,mid,k,val);else insert(tree[x].rc,mid+1,nowr,k,val);tree[x].maxn=max(tree[tree[x].lc].maxn,tree[tree[x].rc].maxn);}
}Tree;int read()
{int d=0; char ch=getchar();while (!isdigit(ch)) ch=getchar();while (isdigit(ch))d=(d<<3)+(d<<1)+ch-48,ch=getchar();return d;
}int main()
{freopen("glo.in","r",stdin);freopen("glo.out","w",stdout);n=read(); m=read();for (int i=1;i<=n;i++)a[i]=read();for (int i=1;i<=n;i++){f[i]=Tree.ask(root,1,Inf,1,a[i]+m-1)+1;Tree.insert(root,1,Inf,a[i],Tree.ask(root,1,Inf,1,a[i]-1)+1);}root=0; Tree.tot=0; Tree.clr(1);for (int i=n;i>=1;i--){Tree.insert(root,1,Inf,a[i]+m,Tree.ask(root,1,Inf,a[i]+m+1,Inf)+1);ans=max(ans,f[i]+Tree.ask(root,1,Inf,a[i]+m+1,Inf));}printf("%d",ans);return 0;
}
这篇关于【JZOJ6310】Global warming【线段树】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


