CF963A Alternating Sum

本文主要是介绍CF963A Alternating Sum，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Alternating Sum

题目传送门

思路：这道题呀，需要涉及到两个数学知识，一是逆元，二是等比数列求和公式。

一：逆元

我们知道 mod 这个东西在题目中时常出现，他可以用于加法，减法，乘法，然而，对于除法，它就不符合了，假定x是a的逆元值，那么b/a%c=b*x%c，就把除法转换成乘法，从而可以运用同余定理，防止计算中的数爆炸，是不是非常的没有用 ，嗯~~~~。

那么怎么求出a的逆元值呢，根据费马小定理，（有兴趣可以证明一下哈），因为小编也没怎么看懂，所以直入主题，简单来说就是b/a % c=b*$a^{(c-2)}$ %c。（前提c是素数）

二：等比数列求和公式

这个高中会学，也比较简单，在小编的范围之内，还是给大家推导一下吧。
假设有个a数列为等比公式，也就是满足ai-1*q=ai (q为公比)

$Sn=a_1+a_2.....+a_n$
Sn * q-Sn=a1 *q+a2 * q…+an * q-a1-a2-a3…-an
Sn * q-Sn=a1 *q+a2 * q…+an * q-a1-a1 * q-a2 * q…-an-1 * q
Sn(q-1)=an * q-a1
Sn(q-1)=a(n+1)-a1
Sn(q-1)=a1 * q^n-a1
Sn=a1(q^n-1)/(q-1)
当然，也可以这样写：Sn=a1(1-q^n)/(1-q)

知识搞定了，那么我们就可以做题了。
大家先看看题目，就会发现S数列长度是k的倍数。
那么我们可以知道S=S1,S2,S3,…,Sk+(S1+…+Sn)。
那么每一个值用下面这个式子来求和
现在我们可以看出对于ai和ai+k来说，他们存在着一定关系
那么带入下面这个式子 Si*A^(n-i)*B ^i
自己推导一下q就为（b/a）^k

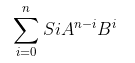
有这些那不就加上个疯狂mod不就大功造成了吗？
上代码：

#include<iostream>
#include<cstdio>
#include<cmath> 
#define N 100001
#define ll long long
using namespace std;
const ll mod=1e9+9;
ll pow1(ll x, ll y){while(x<0)x+=mod;ll ret=1;while(y){if(y&1)(ret*=x)%=mod;(x*=x)%=mod,y>>=1;}return ret;
}
ll n,a,b,k;
char f;
ll s,sum,a1,q,zs;
int main()
{scanf("%lld%lld%lld%lld\n",&n,&a,&b,&k);for(int i=0;i<k;i++){scanf("%1c",&f);if(f=='+') s=1;else s=mod-1;a1=((s%mod*pow1(a,n-i)%mod)%mod*pow1(b,i)%mod)%mod;q=pow1(b*pow1(a,mod-2)%mod,k)%mod;zs=(n+1)/k;if(q==1) sum=(sum+a1*zs%mod)%mod;else sum=(sum+a1*(pow1(q,zs)-1)%mod*pow1(q-1,mod-2)%mod)%mod;}printf("%lld",sum);return 0;	
} 

如有不足之处，请多谅解，小编尽力改进。

这篇关于CF963A Alternating Sum的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---