本文主要是介绍[NOI2011]阿狸的打字机 [AC自动机+树状数组],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
传送门
考虑暴力, 就是将所有为y的fail并且以x结束的点
如果在fail树上考虑呢?
我们发现y到根经过的所有点, 对应到自动机上就是将所有y的fail节点跳一边
如果我们将它们+1, 然后查询子树和, 就相当于在自动机上, 能跳到x的点的个数
我们在fail树上dfs, 显然到了结束的节点就将某一个子串遍历完了, 如果我们把这个子串到根的路径都加1, 那么x在fail树上的子树和
就是x的答案.
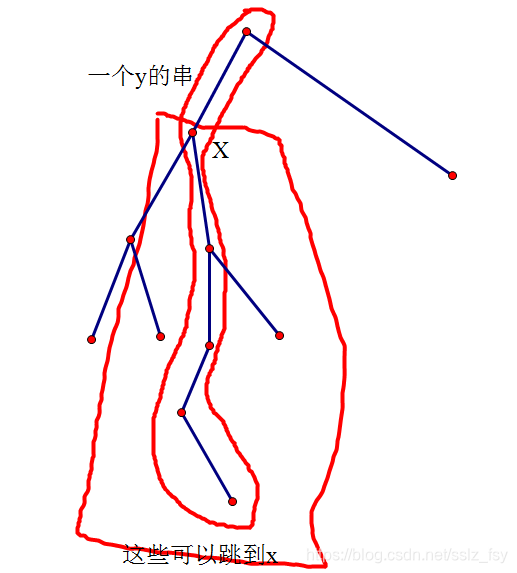
然后dfs序+树状数组就可以了
#include<bits/stdc++.h>
#define N 200050
using namespace std;
char s[N];
int n,tot,num,pos[N],ans[N];
int x[N],y[N];
vector<pair<int, int> > v[N];
int ch[N][26], fa[N], fail[N], p[N];
vector<int> son[N];
int first[N], nxt[N], to[N], ret;
void add(int x,int y){ nxt[++ret] = first[x], first[x] = ret, to[ret] = y;}
int st[N],ed[N],sign;
int c[N];
void Modify(int x,int val){ for(;x<=sign;x+=x&-x) c[x] += val;}
int Quary(int x){int ans=0; for(;x;x-=x&-x) ans += c[x]; return ans;}
void Build(){queue<int> q;for(int i=0;i<26;i++)if(ch[0][i]) q.push(ch[0][i]);while(!q.empty()){int x = q.front(); q.pop();for(int i=0;i<26;i++){int j = fail[x];if(ch[x][i]){ fail[ch[x][i]] = ch[j][i]; q.push(ch[x][i]);}else ch[x][i] = ch[j][i];}}
}
void dfs(int u){st[u] = ++sign;for(int i=first[u];i;i=nxt[i]){int t=to[i]; dfs(t);} ed[u] = sign;
}
void calc(int u){Modify(st[u], 1);int Siz = v[pos[u]].size();if(Siz){ for(int i=0;i<Siz;i++){ int x = v[pos[u]][i].first, id = v[pos[u]][i].second;ans[id] = Quary(ed[p[x]]) - Quary(st[p[x]]-1);} }for(int i=0;i<son[u].size();i++){int t=son[u][i]; calc(t);} Modify(st[u],-1);
}
int main(){scanf("%s%d",s,&n);int len = strlen(s), now = 0;for(int i=0;i<len;i++){if(s[i] >= 'a' && s[i] <= 'z'){int x = s[i] - 'a';if(!ch[now][x]) ch[now][x] = ++tot, fa[ch[now][x]] = now;now = ch[now][x];}if(s[i] == 'P') pos[now] = ++num, p[num] = now;if(s[i] == 'B') now = fa[now];} for(int i=0;i<=tot;i++)for(int j=0;j<26;j++)if(ch[i][j]) son[i].push_back(ch[i][j]);Build();for(int i=1;i<=tot;i++) add(fail[i], i);dfs(0);for(int i=1;i<=n;i++){scanf("%d%d",&x[i],&y[i]);v[y[i]].push_back(make_pair(x[i],i));} calc(0);for(int i=1;i<=n;i++) printf("%d\n",ans[i]); return 0;
}
这篇关于[NOI2011]阿狸的打字机 [AC自动机+树状数组]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




