HDU3716 Jenga

其实是水题啊，不过就是没人做= =

概率+记忆化搜索

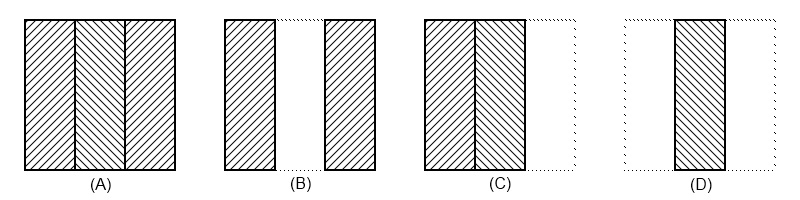
在叠叠乐基础规则之上，已知叠叠乐中每一层只有以上四种状态是稳定的，并且在总高度为n时，积木移动成功的概率为p = b - n * d。

题意就是求在最优策略下，A的胜率。（具体一点请自行读题）

如图，只有A和C两个状态是有后继状态的，所以说我们只需要记录这两个状态的个数就行了。（所以题目中的概率才用b和d表示么= =）

用dp[id][n][m][a][c]记录id还个人在总高度为n，最上一层有m个（其实这个和n差不多，可以互相推，这样写方便嘛= =），下面的层中A状态有a个，C状态有c个。

然后就记忆化搜索就行了= =

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <ctime>
#include <climits>
#include <cmath>
#include <iostream>
#include <string>
#include <vector>
#include <set>
#include <map>
#include <list>
#include <queue>
#include <stack>
#include <deque>
#include <algorithm>
using namespace std;
typedef long long ll;const int maxa = 20;
const int maxc = 40;
const int maxn = 60;
double dp[2][maxn][3][maxa][maxc];
double b[2][3], d[2][3];inline double P(int i, int j, int n)
{return max(0.0, min(1.0, b[i][j] - n * d[i][j]));
}double f(int id, int n, int m, int a, int c)
{double &ret = dp[id][n][m][a][c];if (ret >= 0) return ret;if (a == 0 && c == 0) return ret = 0;int n0 = n, a0 = a;if (m == 0) n++;if (m == 2) a++;m = (m + 1) % 3;ret = 0;if (a0 > 0){ret = max(ret, P(id, 0, n0) * (1.0 - f(1-id, n, m, a-1, c)));ret = max(ret, P(id, 1, n0) * (1.0 - f(1-id, n, m, a-1, c+1)));}if (c > 0){ret = max(ret, P(id, 2, n0) * (1.0 - f(1-id, n, m, a, c-1)));}return ret;
}int main()
{int T, n;scanf("%d", &T);while (T--){for (int i=0;i<2;i++)for (int n=0;n<maxn;n++)for (int m=0;m<3;m++)for (int a=0;a<maxa;a++)for (int c=0;c<maxc;c++)dp[i][n][m][a][c] = -1;scanf("%d", &n);for (int i=0;i<2;i++)for (int j=0;j<3;j++)scanf("%lf%lf", &b[i][j], &d[i][j]);printf("%.4lf\n", f(0, n, 0, n-1, 0));}return 0;
}