本文主要是介绍leetcode_94 Maximal Rectangle,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目:
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
Example:
Input: [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"] ] Output: 6
- 策略: 把matrix看成多个直方图, 每一行及其上方的数据都构成一个直方图, 需要考察matrix.size()个直方图
- 对于每个点(row, col), 我们最后都计算以这个点上方的连续的'1'往left, right方向延申可以得到的最大的矩形的面积
- 通过这种方法获取的矩形一定会把最大的矩形包含在内
- height[row][col]记录的是(row, col)这个坐标为底座的直方图柱子的高度, 如果这个点是'0', 那么高度当然是0了
- left[row][col]记录的是(row, col)这个坐标点对应的height可以延申到的最左边的位置
- right[row][col]记录的是(row, col)这个坐标点对应的height可以延申到的最右边的位置+1
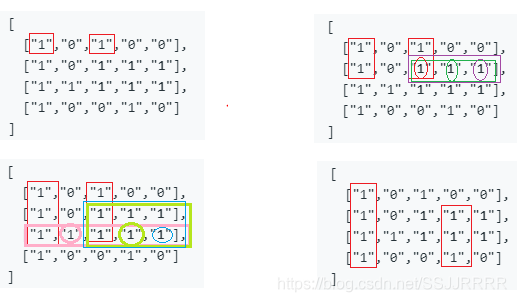
- 以上面的matrix为例,
- 对于(row=2, col=1)这个点, left=0, right=5, height=1
- 对于(row=2, col=2)这个点, left=2, right=3, height=3
- (2,2)这个点与(2,1)紧挨着,left和right却已经变化如此之大了, 这是因为left和right除了受左右两边的'1'影响, 还受到了其上方连续的'1'的制约
- 由于点(2,2)上有height=3个'1', 这几个'1'的left的最大值作为当前点的left, 这几个'1'的right的最小值作为当前点的right
- 因此, 实际上, 我们是要找以hight对应的这条线段往左右两边移动(只能往全是'1'的地方移动), 可以扫过的最大面积
- 当hight与目标最大矩形区域的最短的height重合时, 最大矩形的面积就找到了, 如上面的例子, 就是点(2,3)或(2,4)对应的height
代码如下:
class Solution {
public:int maximalRectangle(vector<vector<char>>& matrix) {if(matrix.size() == 0 || matrix[0].size()== 0)return 0;int m = matrix.size();int n = matrix[0].size();vector<int> height(n,0);vector<int> left(n,0);vector<int> right(n,n);int maxA = 0;for(int i = 0; i < m; i++){int cur_left = 0, cur_right = n;for(int j = 0; j < n; j++){if(matrix[i][j] == '1')height[j]++;elseheight[j] = 0;}for(int j = 0; j < n; j++){if(matrix[i][j] == '1') left[j] = max(left[j],cur_left);elseleft[j] = 0, cur_left = j + 1;}for(int j = n - 1; j >= 0; j--){if(matrix[i][j] == '1')right[j] = min(right[j],cur_right);elseright[j] = n, cur_right = j;} for(int j = 0; j < n; j++){maxA = max(maxA,(right[j] - left[j]) * height[j]);}}return maxA;}
};
这篇关于leetcode_94 Maximal Rectangle的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






