本文主要是介绍数学知识第四期 快速幂,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
快速幂在算法比赛中十分的重要,而且代码简短,清楚易懂,大家应该熟练掌握!!!
一、什么是快速幂?
快速幂是一种高效的算法,用于计算某个数的n次幂。它的基本思想是将原式转换为几个较小的数的乘积,通过递归的方式逐步逼近最终结果。具体来说,对于任意非零整数a和正整数n,快速幂可以通过以下步骤实现:
初始化:令`res = 1`,`base = a`。
重复:直到`n > 0`为止。
判断模性:检查`n & 1`,如果`n & 1`为真,则将`res`乘以`base`并更新`res`;否则不需要修改`res`。
调整基数:将`n /= 2`,同时将`base`减半以准备下一次迭代。
这种算法的时间复杂度为O(log₂N),这比传统的O(N)算法要快得多。快速幂的具体实现可能涉及位运算或其他优化技术,如二分查找或分治策略,以进一步提升性能。
以下是几种不同的快速幂实现方法:
使用位运算和二分查找的快速幂实现:
`int fastPow(int a, int n)`函数示例,使用了`n & 1`来判断模性和调整基数。
另一种更复杂的实现,包括位运算和二分查找,以及使用模运算的简化形式。
使用二叉树的快速幂实现:
通过构建一个二叉树来存储指数部分,并通过递归的方式计算乘积。
使用JavaScript语言的快速幂实现:
利用JavaScript的数据结构如数组和对象来实现快速幂的计算过程。
使用C语言实现的快速幂:
使用`while`循环和位运算来完成快速幂的计算。
这些实现都展示了快速幂的基本思想和实现细节,它们都是为了减少计算次数和时间复杂度,从而提供更高的计算效率
二、例题
1.快速幂
模板:
求 m^k mod p,时间复杂度 O(logk)。int qmi(int m, int k, int p)
{int res = 1 % p, t = m;while (k){if (k&1) res = res * t % p;t = t * t % p;k >>= 1;}return res;
}AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long ;int qmi(LL a, int b, int p)
{LL ans = 1;while (b){if (b & 1) ans = ans * a % p;a = a * a % p;b >>= 1;}return ans;
}int main()
{int m;scanf("%d", &m);while (m -- ){int a, b, p;scanf("%d%d%d", &a, &b, &p);printf("%lld\n", qmi(a, b, p));}return 0;
}
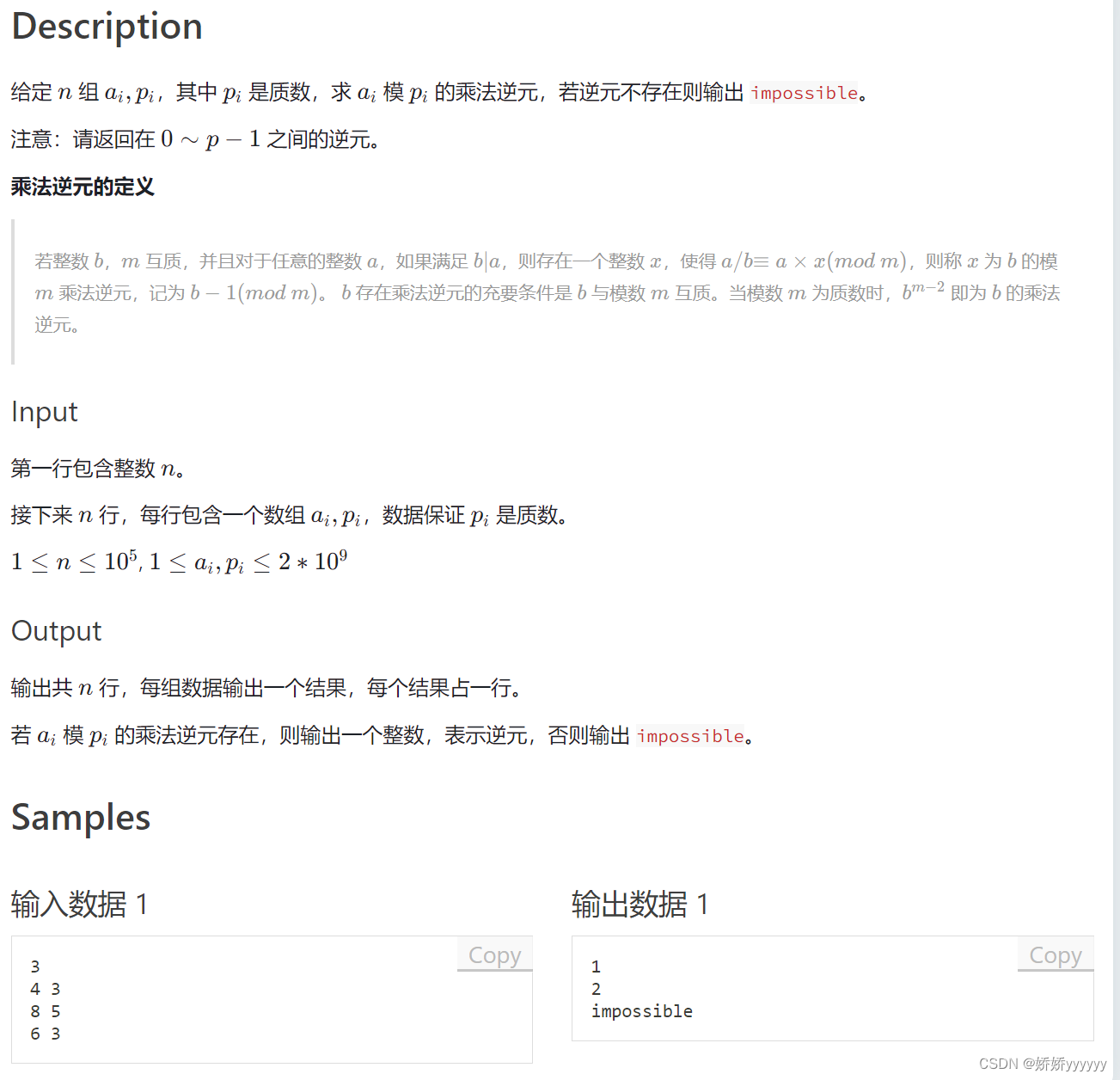
2.快速幂求逆元
AC代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long ;LL qmi(LL a, int b, int p)
{LL ans = 1;while (b){if (b & 1) ans = ans * a % p;a = a * a % p;b >>= 1;}return ans;
}int main()
{int m;scanf("%d", &m);while (m -- ){int a, p;scanf("%d%d", &a, &p);if (a % p == 0) puts("impossible");else printf("%lld\n", qmi(a, p - 2, p));}return 0;
}
总结
快速幂很重要,希望大家能够熟练,感谢大家观看!!!
这篇关于数学知识第四期 快速幂的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!