机器学习-决策树(Entscheidungsbäume)

决策树

基础知识

树的构成：
1.每一个内部节点代表一个属性测试
2.每个分支对应特定的属性值
3.每个叶子节点对应一个分类
树的描述：
对于树通常可以用一个析取范式表示，每一个klausel对应着树上从跟到叶子节点的一条路径
比如：
$(Vorhersage = sonnig \land Luftfeuchtigkeit= normal)\lor(Vorhersage=bedeckt)\lor(Vorhersage=regnerisch \land Wind=schwach)$

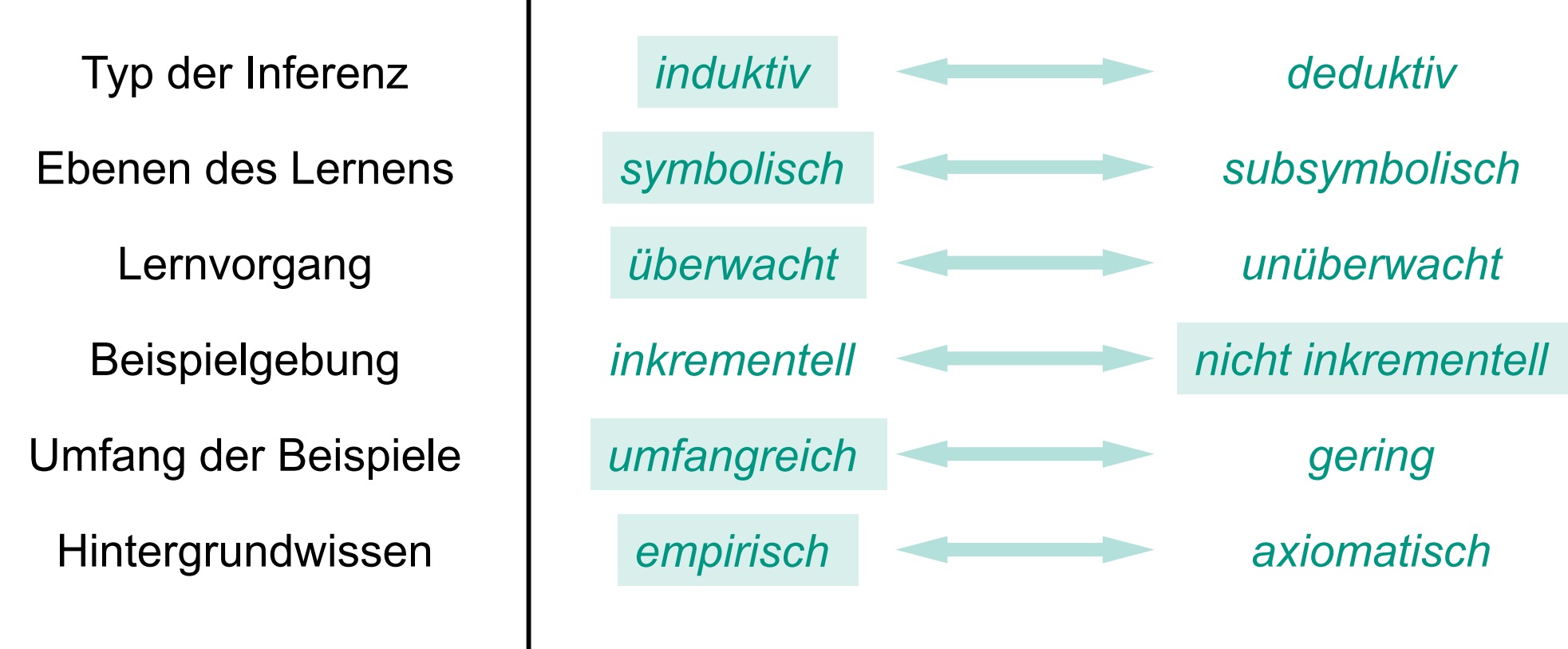
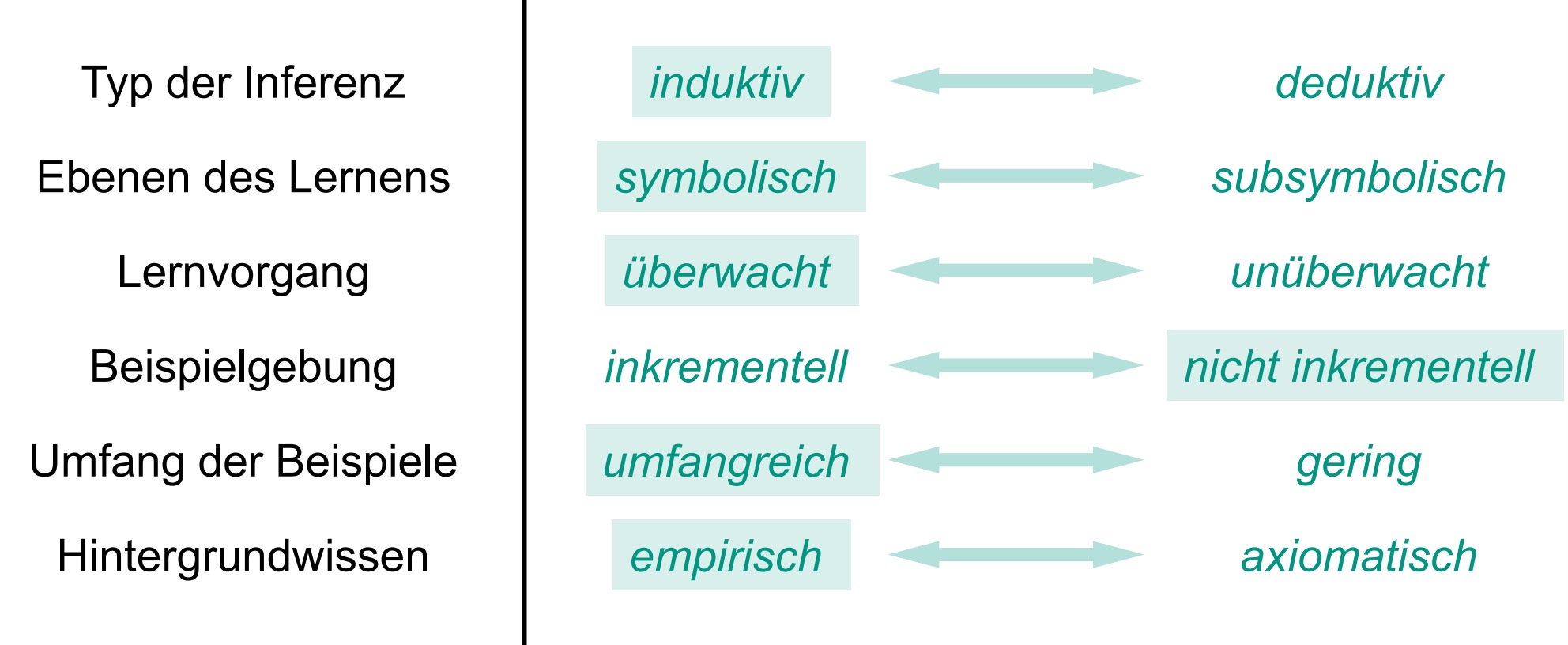
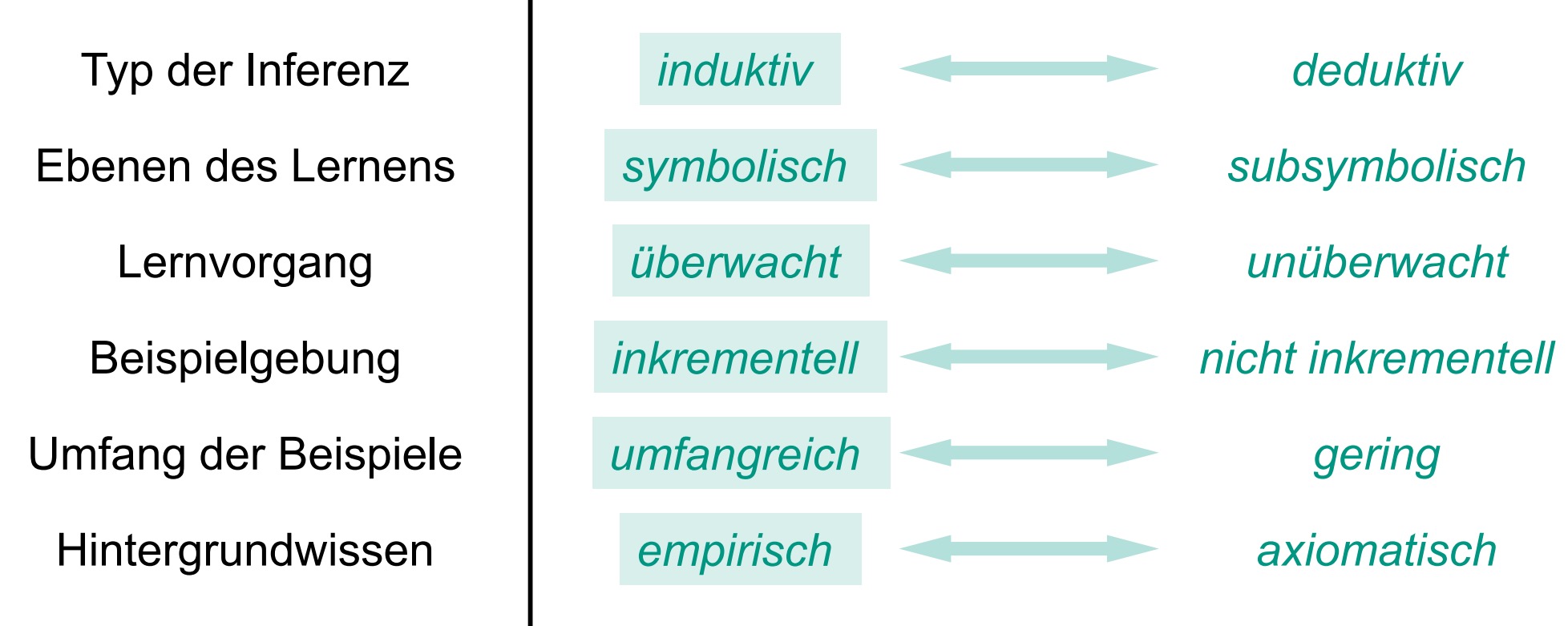
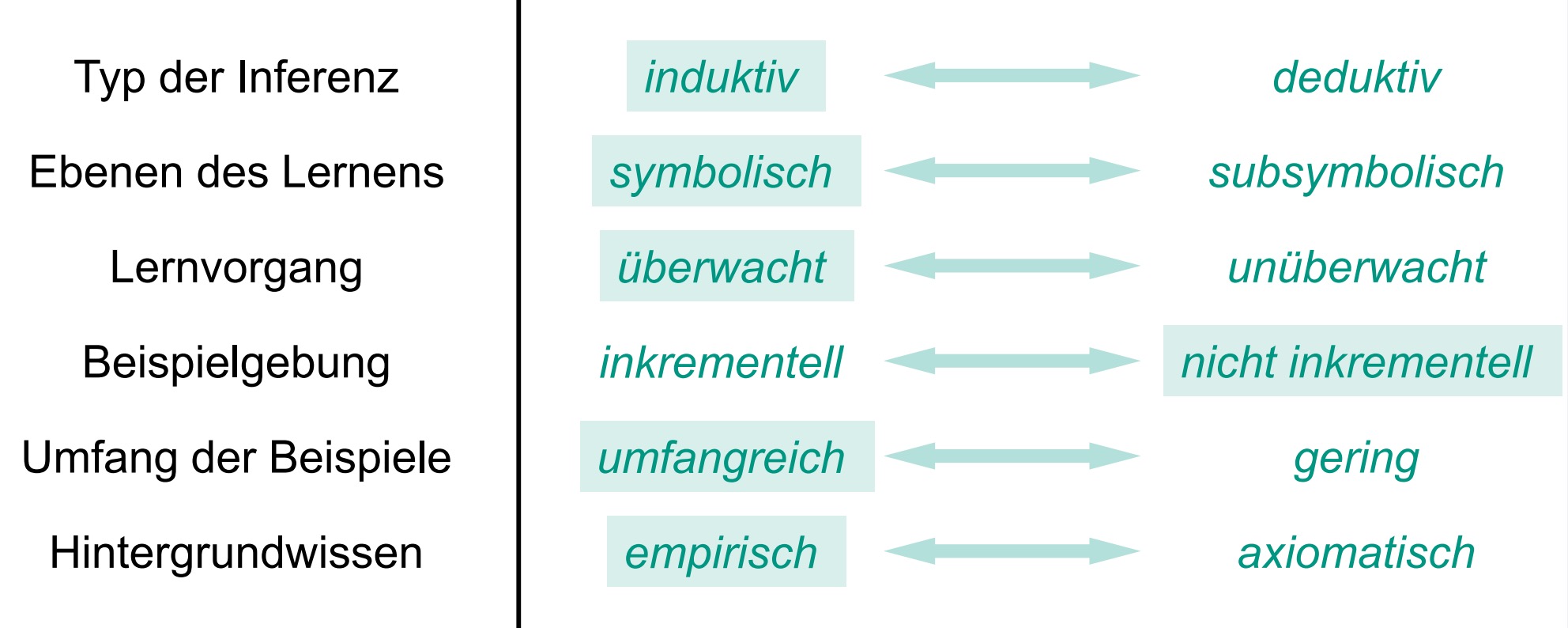
决策树适用范围

1.实例可以用“属性-值”对进行表示的
2.对应输出域是离散的
3.任意两个假设都应该是不相交的(Disjunkte Hypothesen erforderlich)
4.训练用的例子允许存在干扰
(Beispieldaten sind möglicherweise verrauscht)
5.训练用的例子中可能含有错误的属性值
(Beispieldaten enthalten evtl. fehlende Attributwerte)

常用的决策树方法

1.ID3(Quinlan 1986):
非递增方法
(nicht inkrementelles Verfahren)
2.C4.5(Quinlan,1993):
通过一般化规则(剪枝)优化ID3
商业系统//不知何意？？？？
(kommerzielles System)
3.ID5R(Utgoff,1989):
inkrementelles Verfahren
//inkrementell为递增的意思

ID3:从上往下构建决策树

ID3算法的一般表述

1.A$\leftarrow$用于下一步决策的最优的属性
2.把A作为下一步决策用的属性
3.为A的每个可能的取值增加一个后续的节点
(Füge für jeden möglichen Wert von A einen Nachfolgeknoten ein)
//不该啊不是应该就加叶子了吗？？怎么还要加入子节点，感觉这都应该是下一个循环的事了。
4.根据属性值对训练数据进行分类
5.当决策已经能够很好的进行分类时，终止算法。否则则重复上述步骤

熵值(Entropie)

那么应该如何选取最优的测试属性呢？？？
我们用熵值来表示训练数据的齐次性
(Die Entropie als Maß der Homogenität der Trainingsdaten)
//为什么是表示齐次性呢？？？有点搞不懂啊？？？？但是想要干嘛确实知道的。。。。

$$Entropie(S)=-p_{(+)}log_2p_{(+)}-p_{(-)}log_2p_{(-)}$$
其中：
S表示训练集
//前面把例子实例化了，针对的是两类问题，一类用正表示，一类用负表示
$p_{(+)}$表示训练例子中分类为正的部分
$p_{(-)}$表示训练例子中分类为负的部分
//他们正负概率相加不是1吗？？所以有必要两个都写吗？？回到多类问题就有必要了
目标是通过确定属性值v使得正负类尽量的区分开来。也就是说逐渐的缩小对应的熵值。(sukzessive die Entropie maximal zu reduzieren)
//一个属性对应的熵值不是固定的吗？？不应该是找出是熵值最小得属性吗？？另外为什么是就看这个属性的熵值，不应该是求整体的熵值，然后做到全局最优吗？？？

信息增益(Informationsgewinn)

//应该是交信息增益吧，因为说得就是这个意思了，但是和其他的信息增益的公式比起来，怎么就长得不一样呢？？？
Gewinn(S,A):表示通过加入属性A后，熵值减少的量

$$Gewinn(S,A)=Entropie(S)-\sum_{v \in V(A)}\frac{|S_v|}{|S|}Entropie(S_v)$$
V(A)表示A的所有可能的值。
$S_v$表示S对应A取v值的子集
目标是在决策树的深度尽可能浅的情况下是增益最大
例子：S16-18
/*S18-20没看懂不知他要表达的是神马意思
Es gibt typischerweise viele Entscheidungsbäume,die mit den Trainingsbeispielen konsistent sind???
Hypothesenraum ist bei Bäumen vollständig, d.h. Zielfunktion ist enthalten
Suche der Hypothese:,Simple to complex” oder “hill climbing” nach Informationsgewinn???
Lokale Minima(Wie bei allen hill climbing Algorithmen) möglich???
Präferenzbias:
Ordnung auf dem Raum der Hypothesen??
Wähle Hypothese h mit der höchsten Präferenz??
Restriktionsbias:
Einschränkung des Hypothesenraums,z.B. auf lineare Schwellwertfunktionen??
H ist bei ID3 die Potenzmenge der möglichen Instanzen X??
Nicht ganz:
Präferenz für kleine Bäume und für Bäume, deren Attribute nahe der Wurzel einen hohen Informationsgewinn besitzen.
ID3-Bias ist eine Präferenz für bestimmte Hypothesen, aber keinen Restriktion des Hypothesenraums H.???
Occam’s Razor:Bevorzuge die einfachste Hypothese, die mit den Trainingsdaten übereinstimmt.
*/

Occam‘s Razor

Occam’s Razor说得是，相对于长的复杂的假设，更喜欢短的简单的假设
原因是：
1.就数量上而言，短的假设相对于长的来说比较少
2.一个能够正确描述数据的短的假设是巧合的概率比较小
3.和2相反一个比较长的假设，他能够描述这些数据可能只是因为巧合
4.决策树比较小得化效率比较高不是吗

Overfitting

存在问题：

如果在ID3操作过程中：
每个分支都根据增益进行扩展直到所有的都正确分类。
在下面情况下，
1.训练用的例子收到干扰
2.训练例子不具有代表性
不仅会增加复杂度，而且可能存在更多的潜在的错误

Overfitting

定义：
我们说一个假设h对数据D过适应，当存在另一个满足下面条件的可用于替换原假设的假设h’:

$$F_{training}(h) < F_{training}(h')\\ F_D(h)>F_D(h')$$
其中函数F表示存在的错误的数量。

对策

1.提前停止树的扩展
2.生成树后在进行剪枝(实际中比较有用)
确定最优树的大小的标准时什么呢？？
1.分离测试数据
2.对训练数据进行统计测试//这个真不懂要干嘛？？？
/*
Statistischer Test auf den Trainingsdaten
z.B. $x^2$-Test für Unabhängigkeit von Attributen
*/
3.测量训练数据和决策树的编码复杂度//不懂+1
/*
Maß für die Kodierungskomplexität der Trainingsbeispiele und des Entscheidungsbaums
Prinzip der Minimalen Beschreibungslänge
*/

剪枝(Reduced Error Pruning)

1.把数据分为训练数据和测试数据两部分
2.只要剪枝不会导致测试效果表差，就充分下列操作
2.1.用测试数据评价去掉各个节点(及其后续)后决策树的好坏程度
2.2.去掉使决策树提升最多的节点
/*
Evaluiere die Auswirkungen des Entfernens jedes Knotens(und seiner Nachfolgeknoten) auf die Klassifikationsgüte bzgl. der Testdaten.
Entferne den Knoten, dessen Entfernen die Klassifikationsrate bzgl. der Testdaten am meisten erhöht.
*/
$\rightarrow$输出完整子树的最小变形
//不懂？？？？什么叫变形，为什么是子树的变形？？
(Liefert die kleinste Variante des akkuratesten Unterbaums)
存在的问题：
当数据量不足的时候，把数据进行分类可能反而提高了他的出错率(原文是错误的敏感度？？)
(Bei wenigen Daten erhöht das Aufteilen der Daten die Fehlerfälligkeit noch weiter)

值域比较大的属性

存在的问题：
在ID3中通过比较Gewinn(S,A)值域比较大的属性比值域比较小的属性更容易被选作下一个测试的属性
对策：
加如惩罚措施：

$$GewinnAnteil(S,A)\equiv\frac{Gewinn(S,A)}{SplittInformation(S,A)}\\ SplittInformation(S,A)\equiv-\sum^c_{i=1}\frac{|S_i|}{|S|}log_2\frac{|S_i|}{|S|}$$
其中：
$S_i$为S对应A的值为 $v_i$的子集

属性值为连续的

已知：属性A的值是连续的
采取的措施：
动态定义新的离散的属性值$A_c$，并且有：当A>c时，$A_c$为真。

那么现在的问题是：如何选取这个阀值c
我们采用的方法是利用信息增益：
1.按照对应的值的大小，对训练的例子进行排序
(原文应该翻译为分类，但我感觉应该是排序才比较正确吧？？？)
2.如果相邻的两个值属于不同的类，那么最佳的阀值就在这两个值之间。取出所有的符合上面条件的值，计算其各自的信息增益，然后取出增益最大的作为阀值。
//课件里带有一个例子，占地一格。S33

属性值未知

存在的问题是：
如果存在一些属性值并不清楚，那么应该如何使用这些数据呢？？？
//有点模糊，是一个属性所有的属性值都不清楚，还是？？
对应的措施是：
还是用老方法对例子进行分类，缺失的属性值用下面的方法获得：
1.使用例子中对应的最常出现的值
2.使用同一分类的该属性最常出现的那个值
//值还缺着呢是怎么进行分类的？？？
3.取每个值的概率由该值出现的频率决定
(jedem Wert $v_i$ mit Wahrscheinlichkeit $p_i$\rightarrow Verteile das Beispiel gemäß $p_i anteilig auf die Nachfolger(Umsetzung komplexer)$)
在分类时也使用相同的方法

属性的代价

问题是：
测试每个属性都有一定的代价，而且代价不一
(原文是使用不同的代价确定不同的属性值，例子是比如医学诊断，表示理解不能？？？)
对应的措施是：
通过使用下面的式子建立花费比较少的正确的决策树：

$$\frac{Gewinn^2(S,A)}{Cost(A)}\\ $$
或者：
$$\frac{2^{Gewinn(S,A)}-1}{(Cost(A)+1)^w}$$
其中 $w\in[0,1]$代表花费的权重

ID3窗口(ID3:Window)

问题：
当训练数据非常非常巨大时
对应的措施：
1.随机训练集的一个子集(Window)
2.通过这个子集确定对应的决策树
3.用这个决策树对剩余的例子进行分类
4.如果不能全部正确的进行分类，那么就把部分错误分类的例子加入到窗口之中，然后重新生成决策树，重复上面的操作

ID3总结

1.由上向下生成决策树
2.能够表述完整的假设空间
3.偏爱比较小得决策树，和信息增益靠近根节点的决策树
(不知想表达什么，是说生成的决策树大多长这个样子吗？？)
(Induktiver Bias:Präferenz für kleine EB und solche, die Attribute mit hohem Informationsgewinn nahe der Wurzel besitzen)
4.最重要的一个问题就是：过拟合
对应的解决方法是使用剪枝
5.扩展：
当属性值缺失或者是连续的时候应该怎么办
如果每个属性的代价不一样应该怎么弄？？
//缺一图 编号51

C4.5

C4.5的基本知识

1.C4.5是ID3的进一步发展
2.支持连续属性值
3.可以处理缺失属性值的问题
4.使用后剪枝(Post-Pruning)

后剪枝规则(Rule Post-Pruning)

1.像往常一样构建决策树(允许过拟合)
2.把决策树等价转化为If-then规则：
If部分包含了单条路径上得所有的属性测试，Then即包括了对应的输出(分类)
3.只要他的预测能力没有下降，就不断进行(通过减少前置条件)剪枝(一般化)
//是指每次剪都从每一个规则中剪去相同的一个属性吗？？而不是剪去规则吗？？但剪完后应该会有规则是重合的吧？？
(Prune(Generalisiere) die Regeln so lange sich ihre Vorhersagegenauigkeit nicht verschlechtert(durch Entfernen von Vorbedingungen))
4.根据分类能力的好坏对生成的规则进行排序，这个顺序将是你进行预测时使用规则的顺序。
//什么叫规则的分类能力啊，是在说它的熵值吗？？？
//每个规则不是对应着一个类吗，难道预测的方法就是每一条规则都拿出来比对一下啊，那也太多了吧？？？
(Sortiere alle Regeln nach ihrer Klassifikationsgüte und verwende sie in dieser Reihenfolge)

评价规则的好坏

消极评价(Pessimistische Abschätzung)：
1.通过训练数据对规则的好坏程度进行评价
2.使用统计学方法，比如：
2.1.计算标准差
2.2.使用置信区间的下界作为评价的标准
(Verwendung der unteren Grenze des gewählten Konfidenzintervalls als Regelgüte)
//没有懂是怎么弄的？？？

规则的转换

优点：
1.区分了不同的语境，且在这些语境中共用了同一个决策点//不懂？？？？
(Unterscheidung zwischen verschiedenen Kontexten, in denen ein Entscheidungsknoten benutzt wird)
2.不区分一个属性是靠近根节点还是靠近叶子，使剪枝简化
(Keine Unterscheidung zwischen Attributen näher an der Wurzel und solchen näher an den Blättern)
//缺图 编号52

ID5R

关于ID5R的基本知识

1.首先是Utgoff，1989
2.是一个递增的过程，组件引入训练例子来构建决策树
3.结果和用ID3构建的决策树等价

ID5R生成的决策树

回答节点(叶子节点)：
1.类标志，回答是属于哪个类的
2.描述了所有属于这个分类的实例
//感觉应该是描述属于这个节点的实例比较好，因为可能有其他的回答节点也表示相同的分类吧？？？
决策节点：
1.每个属性值都对应一个分支
2.对于每一个属性值保留两个计数器，计算其正的和负的例子的数量
//正负是指分类正确错误还是指分为正的和负的两类
3.除此之外还用计数器记录了对应的还没进行测试的属性。如此在计算每层的信息增益时，就不用回头看知道现在使用过的例子。//不是很懂啊？？增益不是在加入属性时，才计算的吗，什么叫计算每层的增益，使用上下两层的熵值做比较吗？？？
(Zusätzlich Zähler für die noch ausstehenden Attribut-Tests.Ermöglicht Berechnung des Informationsgewinns auf jeder Ebene ohne die bisherigen Beispiele erneut zu betrachten)
//从S47到S59有个大例子 呵呵呵呵

ID5R的树构建算法

已知：
1.当前的决策树：EB
2.新的实例：I
算法：
1.如果EB为空，则加入一个回答节点，其对应的类为实例I对应的类
2.如果EB就是一个回答节点，且该节点对应的类和新的实例对应的类相同，则把这个实例加入到该回答节点的实例集中
3.如果不是上面两种情况，那么就进行以下处理：
a.如果EB就是一个回答节点，那么把他转换成一个决策节点，决策用的属性可以随机选取
b.更新决策节点的计数器(不仅为测试属性，还要为其他属性//严格来说应该不能叫计数器，因为他记录的是实例的信息不是吗，既要更新测试属性的又要更新非测试属性的是为了后面进行信息增益计算)
(Aktualisiere die Zähler des Entscheidungsknotens für Testattribut und alle anderen Attribute)
c.如果测试属性不是最优的(也就是说存在其他属性的信息增益比测试属性的大)，那么进行以下操作：
c.1.对树进行重构，使根节点的测试属性的信息增益最大
(如果增益最大的节点还不是测试节点的话，要先把他从回答节点中扩充出来，然后再把他推到根节点的位置)(注意这时新的实例的信息还没被扩充进去)
(Restrukturiere Baum so, dass Attribut mit höchstem Informationsgewinn Testattribut wird)
c.2.在子树中进行相同的操作，使各个子树中的根节点的测试属性为当前信息增益最大，(这个操作不包括在下一步中要进行更新的子树)
(Wähle Testattribute mit höchstem Informationsgewinn rekursiv in den Unterbäumen)
d.沿着新的实例所在的分支逐层更新信息
重构算法：
加入$A_{new}$为使信息增益最大的属性
1.当$A_{new}$已经在根节点位置，那么结束算法
2.其他情况下，进行以下操作：
2.1.重复的他$A_{new}$推到直接子树的根节点的位置。如果有必要的话，把回答节点转换为以A为测试属性的测试节点。
2.2.这样转化子树，使得在这个树里面，$A_{new}$做为新的根节点，而旧的根节点则为$A_{new}$的直接子节点。
//插图一张 编号53

随机森林(Random Forests)

1.构建多个决策树
要求简单，不相关，随机选择属性(训练数据)
//对前两个形容词表示不解？？？
(Einfach,Unkorreliert,Zufällige Wahl von Attributen)
2.在进行分类时，使用森林中的每个树都进行分类，取出现频率最高的结果作为最终结果
3.性质：
3.1.训练速度快：
因为森林中的每棵树都比较小
随着树的数量的增加，训练时间呈线性增长
3.2.不管在训练时还是在分类时都可以进行并行处理
3.3.对于处理大数据问题效率比较高
(Effizient für große Datenmengen)
4.与一般的决策树比较
4.1.不用进行剪枝，也就是说允许过拟合
4.2.随机选择属性//也就是不用算信息增益？？？
5.生成的决策树的性质
5.1.每棵树本身应该是一个好得分类器
5.2.树与树之间应该尽可能是非关联的//这具体指什么？？
(Die Bäume sollten untereinander möglichst unkorreliert sein)
6.随机化的可能性(Randomisierungsmöglichkeit)
6.1.Bootstraping
//后面两个原因没看懂？？？
6.2.从已知属性的子集中挑选属性测试
Auswahl des Attributtests aus einer Teilmenge der vorhandenen Attributtests
6.3.The main secret is to inject the “right kind of randomness”
//又有图一张 编号54