“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛 F 三角形 python

本文主要是介绍“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛 F 三角形 python，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛 F 三角形
F

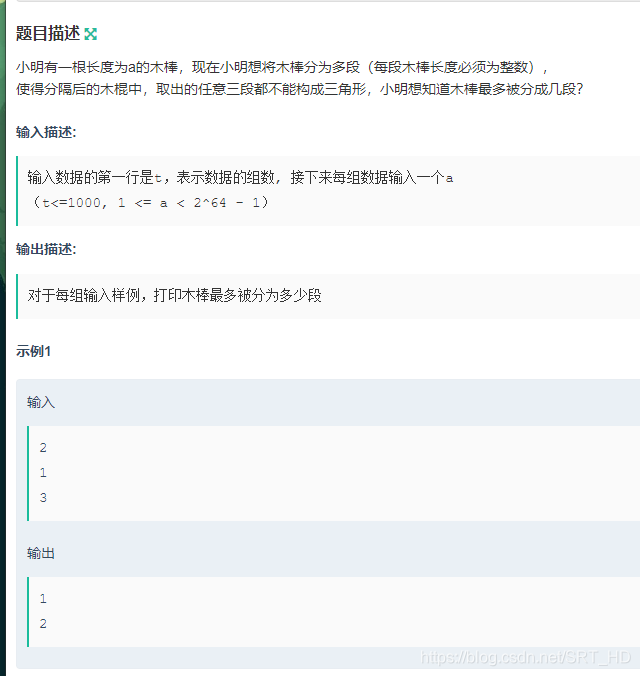
思路： 这里提一个概念是斐波那契数列 顺序如下：1，1，2，3，5，8，13，21，34，55，89，144和无穷大。这个数列从第3项开始，每一项都等于前两项之和
而三角形成立的条件就是 两边之和大于第三边，要不成立 两边和不大即可
而给出的n就是求和，或者再这两个求和之间 （那只需要让最后一个数再大一点就好 ）
然后因为运算怕爆掉，我就直接写了一个斐波那契数的生成函数

斐波那契函数
再进行求和 很巧妙的是 从第三个斐波那契数开始就是第一个斐波那契求和

（可以自己打出来看一下）
不过我偷懒 直接将求和数组带入 然后写（题目要求2⁶⁴ 小于第92个求和）
然后用对分查找 可以省很多时间

代码

for _ in range(int(input())):n=int(input())an=[1 , 2 , 4 , 7 , 12 , 20 , 33 , 54 , 88 , 143 , 232 , 376 , 609 , 986 , 1596 , 2583 , 4180 , 6764 , 10945 , 17710 , 28656 , 46367 , 75024 , 121392 , 196417 , 317810 , 514228 , 832039 , 1346268 , 2178308 , 3524577 , 5702886 , 9227464 , 14930351 , 24157816 , 39088168 , 63245985 , 102334154 , 165580140 , 267914295 , 433494436 , 701408732 , 1134903169 , 1836311902 , 2971215072 , 4807526975 , 7778742048 , 12586269024 , 20365011073 , 32951280098 , 53316291172 , 86267571271 , 139583862444 , 225851433716 , 365435296161 , 591286729878 , 956722026040 , 1548008755919 , 2504730781960 , 4052739537880 , 6557470319841 , 10610209857722 , 17167680177564 , 27777890035287 , 44945570212852 , 72723460248140 , 117669030460993 , 190392490709134 , 308061521170128 , 498454011879263 , 806515533049392 , 1304969544928656 , 2111485077978049 , 3416454622906706 , 5527939700884756 , 8944394323791463 , 14472334024676220 , 23416728348467684 , 37889062373143905 , 61305790721611590 , 99194853094755496 , 160500643816367087 , 259695496911122584 , 420196140727489672 , 679891637638612257 , 1100087778366101930 , 1779979416004714188 , 2880067194370816119 , 4660046610375530308 , 7540113804746346428 , 12200160415121876737 , 19740274219868223166 ,
]i=1j=len(an)while i<=j:m = (i + j) // 2if an[m] - 1 < n: #i==1 但是第一个数的下标是0 为取到中间的数 -1i=m+1else :#小于等于j=m-1a=iprint(a)

然后另一种写法…
再写吧

这篇关于“科林明伦杯”哈尔滨理工大学第十届程序设计竞赛 F 三角形 python的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---