本文主要是介绍Offer必备算法_二分查找_八道力扣OJ题详解(由易到难),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
二分查找算法原理
①力扣704. 二分查找
解析代码
②力扣34. 在排序数组中查找元素的第一个和最后一个位置
解析代码
③力扣69. x 的平方根
解析代码
④力扣35. 搜索插入位置
解析代码
⑤力扣852. 山脉数组的峰顶索引
解析代码
⑥力扣162. 寻找峰值
解析代码
⑦力扣153. 寻找旋转排序数组中的最小值
解析代码
⑧力扣LCR 173. 点名
解析代码
本篇完。
二分查找算法原理
二分查找一种效率较高的查找方法。已经有严谨的数学证明其时间复杂度是O(logN),如果在全国14亿人口中找一个人,那么只需查找31次,但是,二分查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列(无序有时也行,但是要有二段性)。一般步骤如下:
首先,假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功。
以前学C/C++也写过二分查找的代码,直接刷题:
①力扣704. 二分查找
704. 二分查找 - 力扣(LeetCode)
难度 简单
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入:nums= [-1,0,3,5,9,12],target= 9 输出: 4 解释: 9 出现在nums中并且下标为 4
示例 2:
输入:nums= [-1,0,3,5,9,12],target= 2 输出: -1 解释: 2 不存在nums中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
class Solution {
public:int search(vector<int>& nums, int target) {}
};解析代码
首先是有序的,就知道用二分,且这是一道朴素的二分(后面有不朴素的),简单题重拳出击:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;while(left <= right){int mid = left + (right - left) / 2;if(nums[mid] > target){right = mid - 1;}else if(nums[mid] < target){left = mid + 1;}else{return mid;}}return -1;}
};②力扣34. 在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
难度 中等
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
提示:
0 <= nums.length <= 10^5-10^9 <= nums[i] <= 10^9nums是一个非递减数组-10^9 <= target <= 10^9
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {}
};解析代码
非递减,就是数组往后都是大于或者等于的元素,用暴力解法就是找到随便一个端点元素,然后往前往后线性遍历,极端时间复杂度还是O(N),这里用进阶二分的套路(等下总结)
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int size = nums.size();if(size == 0) // 处理边界return {-1, -1}; //返回一个vector里两个整数的方式int left = 0, right = size - 1; // 找左端点while(left < right) // 一定是小于{int mid = left + (right - left) / 2; // 元素个数是偶数时,中点是中间的左边if(nums[mid] < target) // 左端点肯定不在左边left = mid + 1;elseright = mid; // 可能自己是左端点,可能左端点还在左边}if(nums[left] != target) // 没有端点的情况return {-1, -1};int tmp = left; // 记录左端点right = size - 1; // 找右端点,left不用重置while(left < right){int mid = left + (right - left + 1) / 2; // 元素个数是偶数时,中点是中间的右边if(nums[mid] > target) // 右端点肯定右在左边right = mid -1;elseleft = mid; // 可能自己是右端点,可能右端点还在右边}return {tmp, right};}
};以后二分大部分题目都是这个进阶二分的套路,套路就是这样的了(注意两个while的比较):
int left = 0, right = size - 1; // 找左端点while(left < right) // 一定是小于{int mid = left + (right - left) / 2; // 元素个数是偶数时,中点是中间的左边if(nums[mid] < target) // 左端点肯定不在左边left = mid + 1;elseright = mid; // 可能自己是左端点,可能左端点还在左边}if(nums[left] != target) // 没有端点的情况return {-1, -1};int tmp = left; // 记录左端点right = size - 1; // 找右端点,left不用重置while(left < right){int mid = left + (right - left + 1) / 2; // 元素个数是偶数时,中点是中间的右边if(nums[mid] > target) // 右端点肯定右在左边right = mid -1;elseleft = mid; // 可能自己是右端点,可能右端点还在右边}return {tmp, right};③力扣69. x 的平方根
69. x 的平方根 - 力扣(LeetCode)
难度 简单
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 2^31 - 1
class Solution {
public:int mySqrt(int x) {}
};解析代码
暴力解法可以遍历1到X / 2的所有整数,因为这段整数是有序的,所有可以用二分算法,用上一题力扣34总结的进阶二分套路,求右端点:
class Solution {
public:int mySqrt(int x) {if(x <= 1) // 看给的范围处理边界{return x / 1; // 如果是1的话下面right就是0了}int left = 0, right = x / 2;while(left < right){long long mid = left + (right - left + 1) / 2;if(mid * mid > x) // 开long long防溢出{right = mid - 1;}else{left = mid;}}return right;}
};④力扣35. 搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
难度 简单
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
提示:
1 <= nums.length <= 10^4-10^4 <= nums[i] <= 10^4nums为 无重复元素 的 升序 排列数组-10^4 <= target <= 10^4
class Solution {
public:int searchInsert(vector<int>& nums, int target) {}
};解析代码
明显的二分查找,且找左端点:
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size() - 1;if(nums[right] < target) // 找不到就尾插{return right + 1;}while(left < right) // 找不到target就找一个比target大的值,插入到它的前面{int mid = left + (right - left) / 2; // 根据上面注释用二分中找左端点的套路if(nums[mid] < target){left = mid + 1;}else{right = mid;}}return left; // 找没找到都是返回left下标}
};⑤力扣852. 山脉数组的峰顶索引
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
LCR 069. 山脉数组的峰顶索引 - 力扣(LeetCode)
难度 中等
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
提示:
1 <= nums.length <= 10^4-10^4 <= nums[i] <= 10^4nums为 无重复元素 的 升序 排列数组-10^4 <= target <= 10^4
class Solution {
public:int searchInsert(vector<int>& nums, int target) {}
};解析代码
虽然整个数组不是有序的,但是根据单调性可以分出二段性。这里利用二段性把mid归到递增部分,下面就是找右端点:
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {// 虽然整个数组不是有序的,但是根据单调性可以分出二段性// 这里利用二段性把mid归到递增部分,下面就是找右端点:int left = 0, right = arr.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] < arr[mid - 1]) // 如果是递减部分{right = mid - 1;}else{left = mid;}}return left;}
};⑥力扣162. 寻找峰值
162. 寻找峰值 - 力扣(LeetCode)
难度 中等
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-2^31 <= nums[i] <= 2^31 - 1
class Solution {
public:int findPeakElement(vector<int>& nums) {}
};解析代码
注意到是返回任意个峰值都可以,就类似数学的求极大值,那问题就变成上一题力扣852. 山脉数组的峰顶索引了,直接把nums参数改成arr然后复制上一题代码过来就AC了,二段性就是如果找到一个点,如果这个点的右边元素比它小,那么一定有一个极大值在它左边。反之极大值在它右边或者它就是极大值。
class Solution {
public:int findPeakElement(vector<int>& arr) {// 虽然整个数组不是有序的,但是根据单调性可以分出二段性// 这里利用二段性把mid归到递增部分,下面就是找右端点:int left = 0, right = arr.size() - 1;while(left < right){int mid = left + (right - left + 1) / 2;if(arr[mid] < arr[mid - 1]) // 如果是递减部分{right = mid - 1;}else{left = mid;}}return left;}
};⑦力扣153. 寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
难度 中等
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
class Solution {
public:int findMin(vector<int>& nums) {}
};解析代码
二段性就是以最右边元素(下图为D)为标志,如果一个点比它大,那么找的元素肯定在另一边,
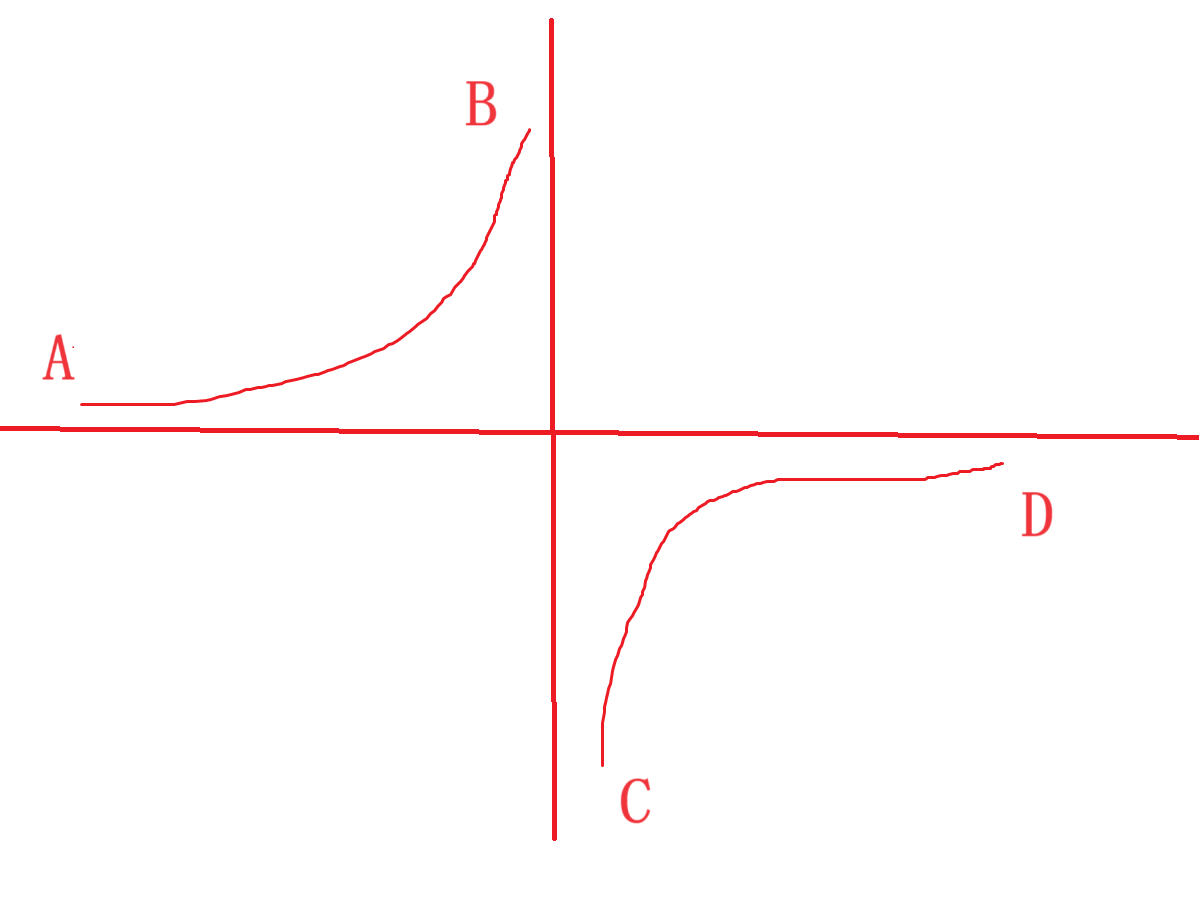
以A为标志也行,但是有边界情况要处理,下面就以D为标志,找左端点:
class Solution {
public:int findMin(vector<int>& nums) {// 二段性就是以最右边元素为标志,如果一个点比它大,那么找的元素肯定在另一边// 以下就是二分找左端点的套路int left = 0, right = nums.size() - 1;int tmp = right;while(left < right){int mid = left + (right - left) / 2;if(nums[mid] > nums[tmp]) // 如果是递减部分{left = mid + 1;}else{right = mid;}}return nums[left];}
};⑧力扣LCR 173. 点名
LCR 173. 点名 - 力扣(LeetCode)
难度 简单
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0,1,2,3,5] 输出: 4
示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8] 输出: 7
提示:
1 <= records.length <= 10000
class Solution {
public:int takeAttendance(vector<int>& records) {}
};解析代码
此题就是以前写过的剑指Offer中数组消失的数字,解法有哈希,遍历,位运算,数学求和,时间都是O(N),二分的解法是O(logN)。
二段性就是找的元素的值肯定不等于数组下标,求左端点的套路:
class Solution {
public:int takeAttendance(vector<int>& records) {// 解法有哈希,遍历,位运算,数学求和,时间都是O(N),二分的解法是O(logN)// 此题二段性就是找的元素的值肯定不等于数组下标,求左端点的套路int left = 0, right = records.size() - 1;if(records[right] == right){return right + 1;}while(left < right){int mid = left + (right - left) / 2;if(records[mid] == mid){left = mid + 1;}else{right = mid;}}return records[left] - 1;}
};本篇完。
下一部分是前缀和算法。
这篇关于Offer必备算法_二分查找_八道力扣OJ题详解(由易到难)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






