本文主要是介绍单片机学习笔记---矩阵键盘密码锁,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,设置密码按键
1.设置密码区域
2.设置输入的数字左移
3.设置记录按键的次数
二,设置确认键
1.密码正确时显示OK
2.密码错误时显示ERR
3.密码错误恢复初始状态重输
三,设置取消键
学了这么久,迫不及待想要做一个密码锁玩一玩,那直接进入正题!
这节我们可以直接创建一个跟上一节一模一样的工程文件。
可以直接复制粘贴上一节的工程文件,把名字改成矩阵键盘密码锁就可以了。
然后点击打开这个文件,就得到一个一模一样的工程了。
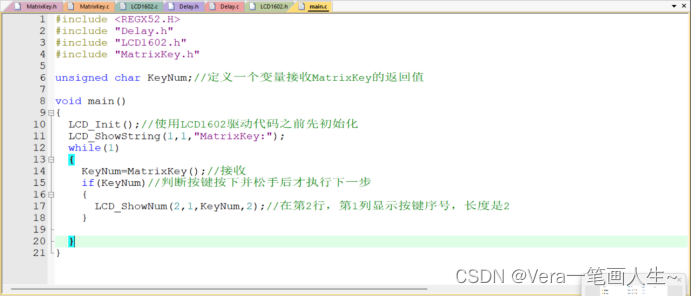
然后把上一节课的这一句代码改成Password


然后编译测试一下

没有错,可以继续了!
一,设置密码按键
我们想要把S1-S9定义为数字1-9,然后S10定义为0,为什么没有S0呢?
是因为0这个数字被占用了,作为一种没有按键按下的返回。
所以我们就把S10定义为0,S11作为确认键,S12作为取消键,S13-S16键不用。
开始写代码:
1.设置密码区域
需要再加一个if判断限制密码区
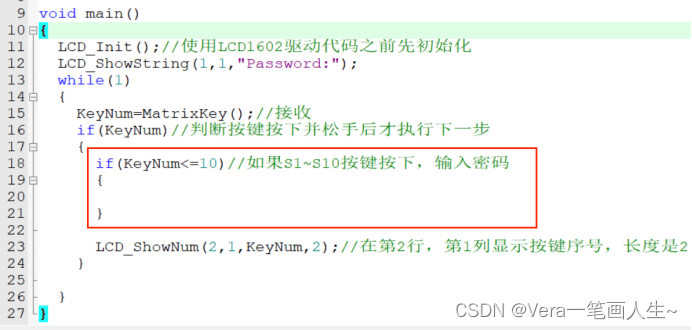
然后定义一个密码变量,类型是unsigned int,为什么是unsigned int?是因为它的取值范围是0-65535,为什么我们这个程序不用6位密码?因为六位的话已经超出unsigned int的取值范围了。
如果定义一个5位数的密码是99999的话就存不了,当然也可以改成unsigned long long类型,但是这样还受限于我们的LCD1602.c中的定义的LCD_ShowNum只支持0-65535,所以6位密码不好显示。

当然,如果你想的话也可以显示,比如可以定义一个数组,然后一位一位分开存,然后一位一位地显示。
但是为了简单,本节只显示4位密码,这样Unsigned int完全可以存的下了。
代码这样写

这里还需要改成Password
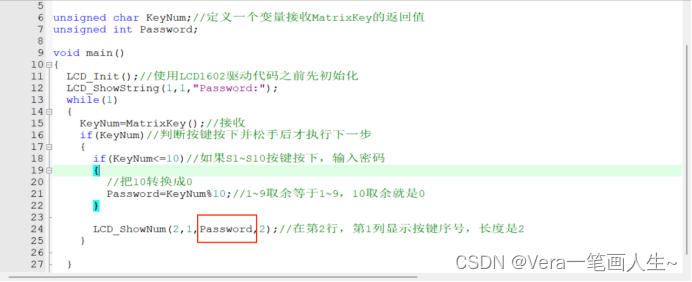
编译测试一下
按下9,松开就显示09

按下10松开就显示0

证明这段代码没有问题,继续!
2.设置输入的数字左移
我们需要把输入的上一个数字挪到左边去,代码这样写:
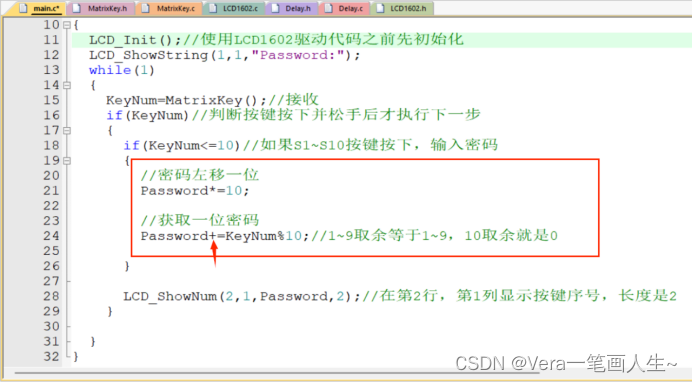
为什么这样写呢?
比如密码刚开始等于0000,然后输入一位密码1,按下1后就变成0001
如果再按下2,0001*10就变成 0010,再加上2,就是0012
如果再输入3,就是0012*10变成0120,再加上3,就是0123
搞明白了后,把先显示密码长度改成4
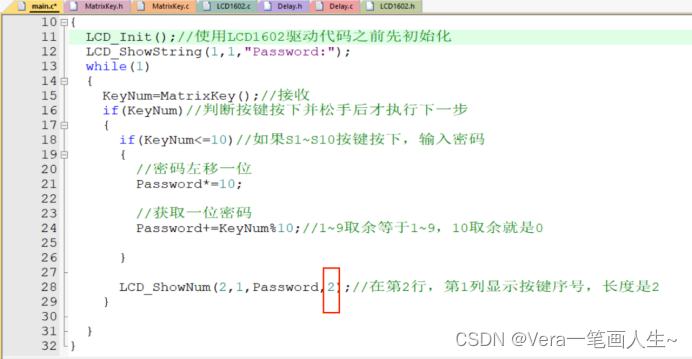
编译测试一下:


一次按下1 2 3 4后,屏幕上显示1234,效果正确!
如果再继续按5的话,最高位的1就不见了

如果按6的话,就显示错误,是因为超出了取值范围,就显示别的了。

3.设置记录按键的次数
所以我们接下来要写一段程序判断按下的次数
当输入超过4位,就不让用户继续输入了。
再定义一个变量Count用来计数:
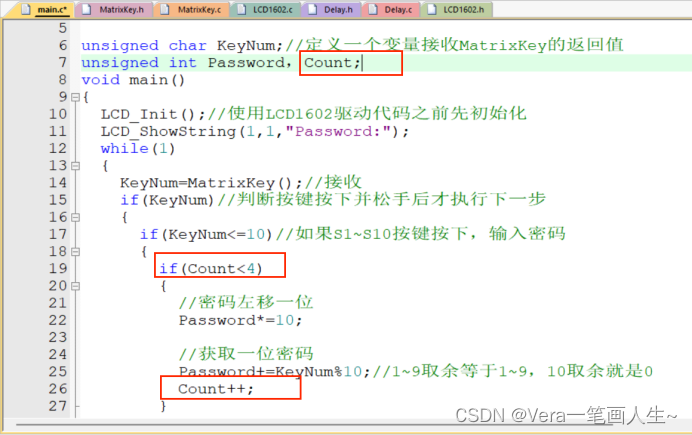
测试一下:

当按第五次的时候,就不再有反应了,是我们想要实现的效果!
我们可以把这段代码挪上来


二,设置确认键
1.密码正确时显示OK
然后再加一个if判断,如果按下的密码正确则显示OK
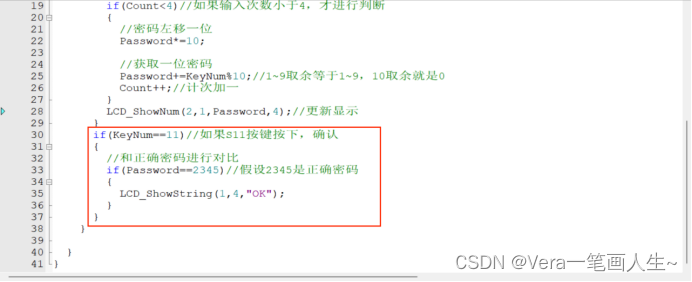
测试一下:

正确!
2.密码错误时显示ERR
如果输入的密码不正确,就显示err错误

测试一下:

不等于正确密码,显示err
3.密码错误恢复初始状态重输
提示错误后,还得让人家继续输入,所以要恢复初始状态
正确与否都应该清零,才能让人重新输入。
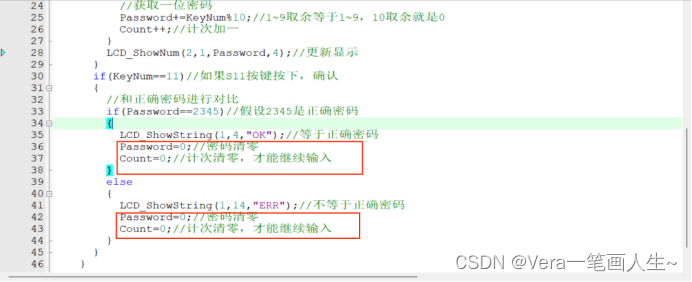
测试一下:
按下1234后,显示错误

但是显示没有清零,但其实变量已经清零
所以我们还需要更新一下显示:

再测试一下:

输入1234错误后,提示ERR,并清零

重新输入2345,按下确认

显示OKR,并清零

为什么是显示OKR不是OK?
因为我们前面输错密码显示了ERR,现在显示OK才占两个字符,可以在OK后面加个空格占一个字符,覆盖R

再测试一下:

这样就没有多出来一个R了
三,设置取消键
接下来还需要设置一个取消键,如果人家输到一半密码发现输错了,按取消,重新输。
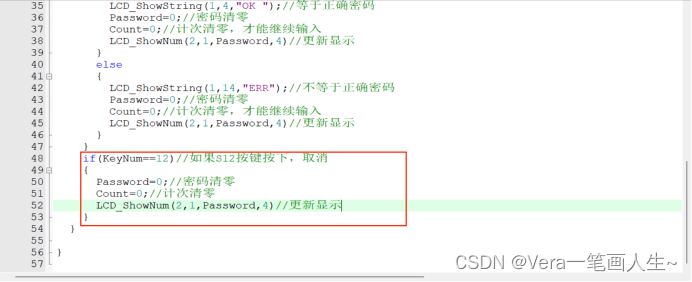
测试一下:
输入2345,点取消

什么都没有显示,直接清零

输1234,点击确认显示ERR

输2345,点击确认,显示OK

OK和ERR都会清零
以上就是本节想要实现的效果。
这节的代码比较多,如果出错,可以最好是边写边测试。
本节所有的程序源码评论区自取。
如果有问题可以私信我评论区留言,谢谢!
这篇关于单片机学习笔记---矩阵键盘密码锁的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








