上海市计算机学会竞赛平台（iai.sh.cn）十二月月赛（丙组）解题报告

多边形的内角和

内存限制: 256 Mb时间限制: 1000 ms

题目描述

一个 n 条边的多边形，其内角和公式为 $180\times (n-2)$。给定 n，请计算并输出 n 边形的内角和。

输入格式

单个整数：表示 n。

输出格式

单个整数：表示 n 边形的内角和。

数据范围

$3\le n\le 100$

样例数据

输入:

3

输出:

180

输入:

5

输出:

540

解题思路

根据上述公式，输出即可。

代码实现

#include <bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;cout<<(n-2)*180<<endl;return 0;
}

星号三角阵（二）

内存限制: 256 Mb时间限制: 1000 ms

题目描述

给定一个整数 n，输出一个 n 行 n 列的星号三角阵，直角位于图形的左上角。例如当 n=4 时，输出

****
***
**
*

输入格式

单个整数表示 n。

输出格式

共 n 行：表示一个星号三角阵。

数据范围

$1\le n\le 100$

样例数据

输入:

3

输出:

***
**
*

解题思路

第$i$行输出$n-i+1$个$\ast$

代码实现

#include <bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=n-i+1;j>=1;j--)cout<<"*";cout<<endl;}return 0;
}

折纸

内存限制: 256 Mb时间限制: 1000 ms

题目描述

小爱手中有一张矩形纸张，他想把这张纸分成若干正方形纸片，具体分法如下：

第1步：小爱会先确定纸张的长宽，假设短边长度为n，长边长度为m。
第2步：小爱会将短边沿直角平分线对折后剪去，从而得到一个$n\times n$的方形纸片。
第3步：若还有剩余，小爱会将剩余的长宽为$n\ast (m-n)$的纸张作为现有纸张，代入第一步后重复之前过程，直至没有之后纸张剩余为止。
请问按如上操作，小爱最终会得到几张方形纸片？

例如：一开始，小爱有一张 $10\times 6$ 的纸张，按他的分割方法，最终他可以获得 4 张方形纸片，具体过程如下图所示：

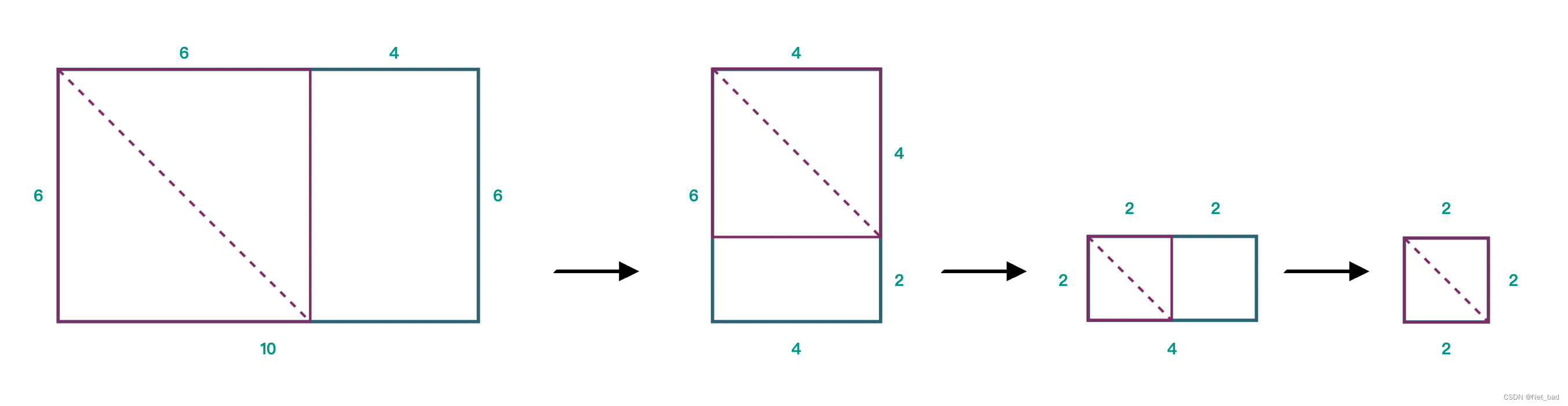
输入格式

输入共两个正整数，表示初始矩形纸张的长宽 n,m

输出格式

输出题目所求能获得的矩形个数

数据范围

对于 $30\%$ 的数据，$1\le n,m\le 100$
对于 $60\%$ 的数据，$1\le n,m\le 10^7$
对于 $100\%$ 的数据，$1\le n,m\le 10^{13}$

样例数据

输入:

10 6

输出:

4

解题思路

取n,m中较大的数为长，另一个为宽，然后不断地

• $n=max(n-m,m)$
• $m=min(n-m,m)$

直到$n=m$即可,但是ans要赋初值为1，因为最终总会多折出一个正方形

代码展示

#include <bits/stdc++.h>
using namespace std;long long n,m,ans=1;int main(){cin>>n>>m;long long a=n,b=m;n=max(a,b);m=min(a,b);while(n-m!=0){long long a=n,b=m;n=max(a-b,b);m=min(a-b,b);ans++;}cout<<ans<<endl;return 0;
}

但是，我们这里犯了一个非常重大的错误，我们在之前的比赛中曾翻过一个错误，就是当n无穷大时，m无穷小时，就会超时，所以我们上面的代码在最终评测中只得到了60分。

优化思路

我们完全可以通过算式求出一个长方形可以切出多少个宽度为m的正方形，然后再将长和宽转换一下即可

代码展示

#include <bits/stdc++.h>
using namespace std;long long n,m,ans=0;int main(){cin>>n>>m;while(true){ans+=n/m;long long f=n%m;if(f==0)break;else{n=m;m=f;}}cout<<ans<<endl;return 0;
}

中位数（二）

内存限制: 256 Mb时间限制: 1000 ms

题目描述

中位数，就指将所有数字排序后，位置在最中间的数。

给定 n 个数字的序列 $a_1,a_2,...,a_n$
，以及一个期望中位数 x。小爱想知道，最少再添加多少个数字，才能使序列中包含奇数个数字，且 x 为该序列的中位数？

输入格式

输入共三行：
第一行，一个正整数 n ，表示元素个数
第二行，n 个整数，分别表示 $a_1,a_2,...,a_n$
第三行，一个整数 x ,表示期望中位数

输出格式

输入一个整数，表示答案

数据范围

对于 $30\%$ 的数据， $1\le n\le 100$
对于 $60\%$ 的数据， $1\le n\le 10^4$
对于 $100\%$ 的数据， $1\le n\le 10^5$

样例数据

输入:

4
6 4 7 1
3

输出:

3

说明:

加1个3 和 2个1，就可以让3成为中位数

输入:

5
1 2 3 4 5
3

输出:

0

说明:

不用添加任何数字，3已经是中位数

解题思路

我们可以先排个序，然后在输入的数列中寻找是否有$x$，如果没有的话输出的$ans$就要多一个，然后再将小于$x$的数和大于$x$的数分别用$left$和$right$记录下来，然后如果x有多个，就用$time$变量记录下来，然后如果$left>right$，就将$right$加上$time-1$，反之，$left$加上$time-1$。最终输出$ans+abs(left-right)$

代码实现

#include <bits/stdc++.h>
using namespace std;const int MAXN=1e5+10;int n,a[MAXN],x,ans;int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];cin>>x;bool f=false;int time=0;for(int i=1;i<=n;i++){if(a[i]==x){f=true;time++;}}if(!f){a[n+1]=x;sort(a+1,a+n+1);ans=1;}else{sort(a+1,a+n);ans=0;}int left=0,right=0;for(int i=1;i<=n;i++){if(a[i]<x)left++;else if(a[i]>x)right++;}
//	cout<<"L:"<<left<<endl;
//	cout<<"R:"<<right<<endl;if(left>right){if(time>1){right+=time-1;}}if(left<right){if(time>1){left+=time-1;}}cout<<ans+abs(left-right)<<endl;return 0;
}

等差数列

内存限制: 256 Mb时间限制: 1000 ms

题目描述

等差数列 指从第二项起，每一项与它的前一项的差等于同一个常数的一种数列，且这个常数叫做等差数列的公差。

例如：数列 1 5 9 13 就是一个公差为 4 的等差数列。

现给定一个长度为 n 的序列 $a_1,a_2,...,a_n$ ，请问该序列中，有多少个长度不小于 3的子段满足等差数列？

输入格式

输入共两行：
第一行，一个正整数 n，表示给定序列长度
第二行，n 个整数，分别表示序列的每一项 $a_1,a_2,...,a_n$

输出格式

输出一个整数，表示满足条件的子段个数。

数据范围

对于 $30\%$ 的数据， $1\le n\le 1001\le n\le 100$
对于 $60\%$ 的数据， $1\le n\le 10^4$
对于 $100\%$ 的数据， $1\le n\le 10^5,-10^9\le a_i\le 10^9$

样例数据

输入:

10
-1 1 3 3 3 2 3 2 1 0

输出:

5

说明:

区间[1,3],[3,5],[7,10],[7,9],[8,10]均满足等差数列要求

解题思路

先将这组数列的差分求出来用另一个数组存着，然后把差分数组相等的个数记录下来，然后如果相等ans++，否则用求和公式将数列中ans个数的所有排列方式算出来，用rl吧结果加上，然后ans变回原值。输出rl即可

代码实现

#include <bits/stdc++.h>
using namespace std;
#define int long longconst int MAXN=1e5+10;int n,a[MAXN],b[MAXN],ans,rl=0;signed main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<n;i++){b[i]=a[i+1]-a[i];}ans=2;
//	for(int i=1;i<n;i++)
//		cout<<b[i]<<" ";for(int i=1;i<n;i++){if(b[i]==b[i+1])ans++;else{if(ans>=3){rl+=(ans-1)*(ans-2)/2;}ans=2;}}cout<<rl<<endl;return 0;
}